浅谈树旋转

目录

• 一些 update
• 1.概述
• 2.旋转
  • 2.1 总览
  • 2.2 右旋
  • 2.3 左旋
• 3.代码

一些 update

update 2021/1/2：加入代码解释。

update 2021/1/13：发现『2.3 左旋』图片有重大失误，现在已经更正，对各位读者带来的不便深表歉意。

1.概述

树旋转，是 AVL 树和 Splay 等平衡树控制平衡的一种办法，同时也在别的领域有着重要的应用。

那么什么是树旋转呢？又有什么类型呢？

2.旋转

2.1 总览

比如下面这两棵树，上面的树对 0 号节点右旋后成为下面的树，下面的树对 1 号节点左旋后成为上面的树。

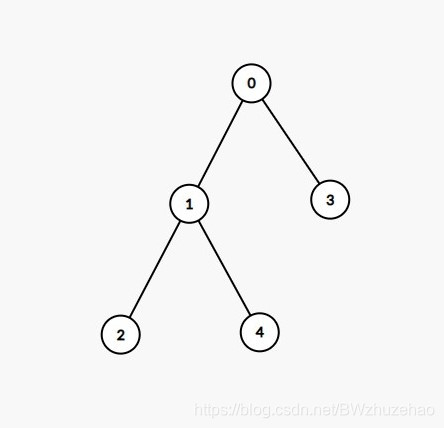
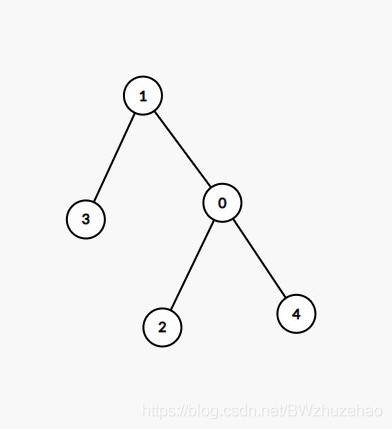
那么怎么做树旋转呢？这里给大家一句口诀（也是我从一些算法视频上学到的，并非原创）：左旋拎右左挂右，右旋拎左右挂左。

什么意思呢？别急，等我细细道来。

2.2 右旋

首先我们看看右旋操作。

右旋拎左右挂左，那么第一步：拎左。

这是一开始的树：

那么我们对 0 号节点右旋，首先“拎左”：将左子树拎起来。

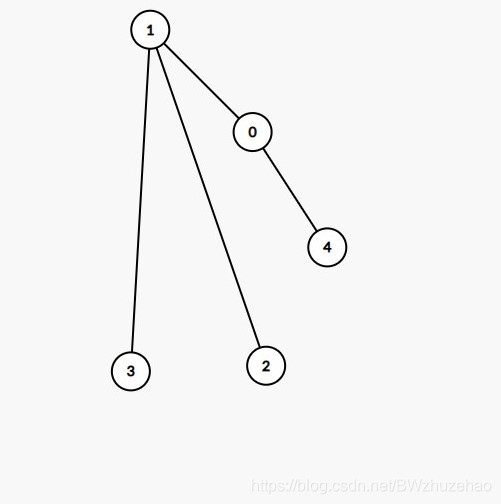
从上可以看到，在“拎左”之后 1 号节点现在是 0 号节点的父亲。

然后要“右挂左”：将拎起来的节点的右子树挂到需要旋转的节点的左子树上，在图中就是将 2 号节点挂到 0 号节点的左子树下，就是这样：

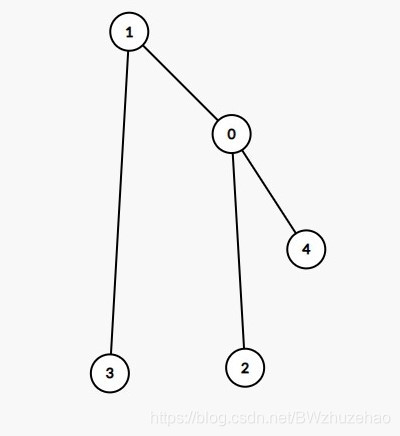
然后把树弄好看一点，就变成了这样：

那么现在你也应该猜到要怎么左旋了。

2.3 左旋

我们对上图的 1 号节点左旋。

左旋拎右左挂右。

首先“拎右”：我们将 1 号节点的右子树拎起来，像这样：

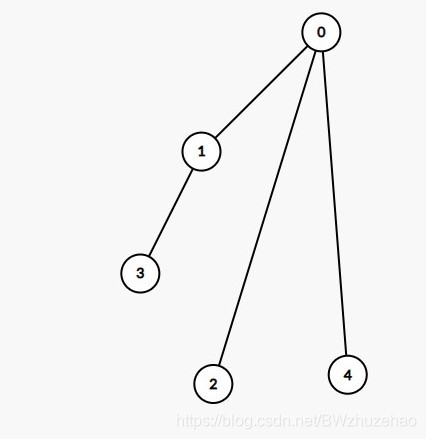
然后“左挂右”：将被拎起来的节点的左子树挂到需要旋转的节点的右子树上，也就是将 2 号节点挂到 1 号节点上，就是这样：

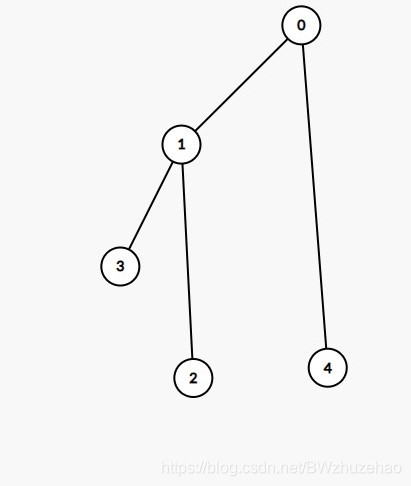
最后把树弄好看一点，就变成了这样：

所以这就是树旋转。

3.代码

代码（作者从 AVL 树上复制过来的）：

void lrotate(int &now)//左旋
{
	int r = tree[now].r;//注意临时保存
	tree[now].r = tree[r].l;//左挂右
	tree[r].l = now;//拎右
	now = r;//拎右
	update(tree[now].l), update(now);//注意顺序
}

void rrotate(int &now)//右旋
{
	int l = tree[now].l;//注意临时保存
	tree[now].l = tree[l].r;//右挂左
	tree[l].r = now;//拎左
	now = l;//拎左
	update(tree[now].r), update(now);//注意顺序
}