DP专题-学习笔记：Slope Trick
1. 前言
Slope Trick，是一种优化 DP 的方式，这个方式目前好像并不盛行，但是以前好像还挺流行的（？），网上讲 Slope Trick 的博客好像也不多（？）。
- （？） 表示笔者持怀疑态度，也就是说这句话可能是错的。
现在笔者得知的能够使用 Slope Trick 的题目并不多，这里主要讲 CF 的一道题，好像是已知的 Slope Trick 最早出现的时间（2016 年）（？）。
注意 Slope Trick 不是斜率优化 dp，这两个是不同的算法。
2. 详解
先放例题：CF713C Sonya and Problem Wihtout a Legend。
简要题意：给定 \(n\) 个正整数 \(\{a_i\}\)，每次操作可以将任意一个元素加一或减一，问使得原序列严格递增的最小操作次数。
当然我们需要加强到 \(n \leq 10^5\)，否则这个能用 \(O(n^2)\) DP 暴力解决。
首先发现严格递增这个东西我们有一个套路的方式就是令 \(a_i \leftarrow a_i-i\)，于是这样就变成了严格不降。
然后我们有一个简略的 DP 方程：
设 \(f_{i,j}\) 表示将 \(a_i\) 变成 \(j\)，使得 \([1,i]\) 的数列不降所需要的最小操作次数，那么有：
这个 DP 方程还是比较简单的吧~
这样，我们就能够在 \(O(n^2)\) 的复杂度内赛时解决这道题，当然在 \(n \leq 10^5\) 的情况下是过不了的。
此时 Slope Trick 就可以派上用场了。
首先我们需要知道 Slope Trick 能够优化什么问题：通常情况下，Slope Trick 能够解决的是一类凸函数问题。
啥意思呢？
比如说这道题的 DP 方程，我们首先转变一下式子：记 \(F_i(x)\) 为 \(f_{i,x}\)，定义 \(G_i(x)=\min_{1 \leq k \leq x}f_{i,k}\)。
那么式子就是 \(F_i(x)=G_{i-1}(x)+|a_i-x|\)。
然后仔细研究这个函数，我们会发现这个函数有下凸性质，画出来大概是这个样子：
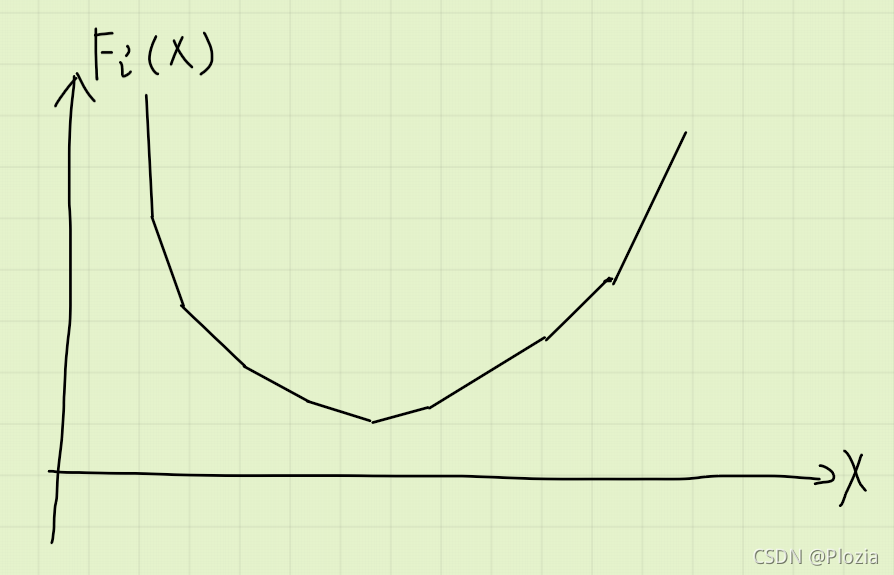
需要注意的是，前面 \(F_i(x)\) 递减部分确实是个下凸包，但是后半部分不一定。
我们记 \(h(i)\) 表示当 \(x=h(i)\) 时 \(F_{i}(x)=G_{i}(x)\)，也就是函数 \(F_{i}(x)\) 取到最小值的地方。
然后我们重新看一下这个方程：\(F_i(x)=G_{i-1}(x)+|a_i-x|\)。
我们发现这个式子很有意思：我们只需要快速维护 \(G_i(x)\) 就可以了。
具体怎么维护呢？
其实对于这种分段函数且各函数都是一次函数的情况下，有一种快速的方法维护最小值：维护所有分段点以及最右端一次函数即可。
比如说还是上图，可以发现我们只需要维护下图的红点和红线即可：
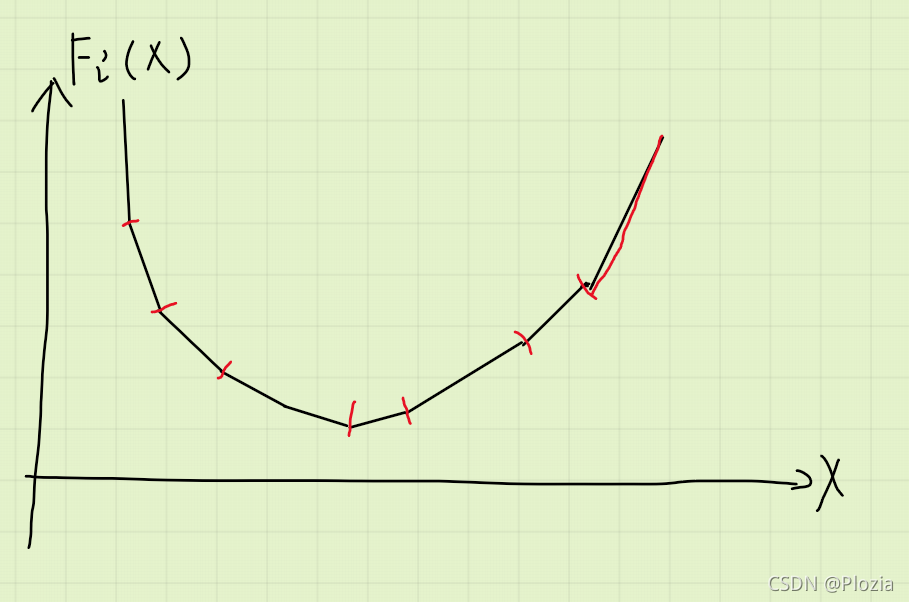
特别需要注意的是如果两个相邻段的斜率之差大于 1，那么这个关键点是要存两遍的。
那么现在我们来讨论如何通过所有已知的 \(F_{i-1}(x)\) 和 \(G_{i-1}(x)\) 来快速维护 \(F_{i}(x)\)。
有几个关键点：
- 我们画出 \(F_i(x)\) 的大致图像后，结合状态转移方程，发现在 \(h(i)\) 前的所有函数斜率递减，在 \(h(i)\) 之后的所有函数斜率递增。
- 其实 \(F_i(x)\) 是在 \(F_{i-1}(x)\) 上的叠加。
- \(h(i)\) 处这个点左右两个函数的斜率一个是正的，一个是负的。
- 实际上所有斜率为正的点在计算的时候是无用的，因为我们的转移是从 \(F_{i-1}(x)\) 转移到 \(F_i(y),x \leq y\)，所以我们需要 \(F_i(y)\) 数据的时候完全可以直接从 \(F_{i-1}(x)\) 推过来。
根据上面的第四点，我们只需要维护所有左边的函数斜率小于 0 的关键点即可，也就是下面这些蓝色的点：
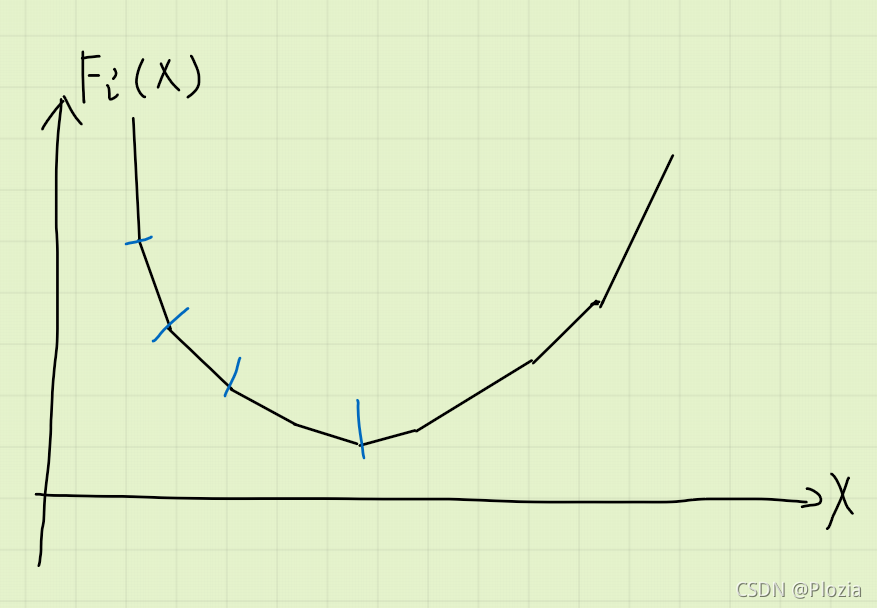
然后我们讨论一下 \(h(i-1)\) 和 \(a_i\) 的关系：
- \(h(i-1) \leq a_i\)
这个情况下你会发现，我们在函数叠加的时候，所有 \(x < h(i)\) 的点其纵坐标之差加一，用式子表达就是所有 \(F_i(x)-F_i(x-1)\) 都降低了 1，从斜率角度来看就是斜率全部递减 1。
从贪心的角度来理解，此时此刻你没必要将 \(a_i\) 减小到 \(h(i-1)\)，因为这个时候 \(h(i)=a_i\)，肯定是当前最优的解。
至于如果后面的 \(a_{i+1}\) 远小于 \(a_i\)，那就是另外一个情况要讨论的事情了。
于是我们只需要将 \(a_i\) 这个点丢进我们的关键点里面，然后这个点就做完了。
- \(h(i-1)>a_i\)
这个时候我们发现我们需要将 \(a_i\) 提升到 \(h(i-1)\) 才能够做到序列单调不降，因此这一块的贡献是 \(h(i-1)-a_i\)。
然后我们发现对于所有 \(x<a_i\)，所有 \(F_i(x)-F_i(x-1)\) 都降低了 1，而对于所有 \(h(i-1) \geq x>a_i\)，，所有 \(F_i(x)-F_i(x-1)\) 都升高了 1，这个同样也能从斜率角度来理解。
此时我们发现在 \(a_i\) 这个关键点出现了问题，因为这个时候整个函数已经被改变了，由于 \(h(i-1)>a_i\)，此时 \(a_i\) 这个地方左右斜率相差大于 1 了，因此我们需要将 \(a_i\) 两次丢进我们的关键点里面。
最后将 \(h(i-1)\) 丢出队列，因为这个时候在 \(h(i-1)\) 这个地方因为 \(a_i\) 的影响使得最后的位置斜率升高了，这个点不再是我们的最小值点了（\(h(i) \neq h(i-1)\)），所以我们需要将 \(h(i-1)\) 丢出队列。
有人可能会问：会不会存在在一个同样的值 \(x\) 出现 4 个或者更多的关键点都是 \(x\) 呢？
这个情况吗……emm……确实是存在的，但是我们需要知道这道题的一个显然结论：
- 将 \(a_{i-1}\) 改到 \(a_i\) 和将 \(a_i\) 改到 \(a_{i-1}\) 的贡献是一样的。
据此，实际上我们会发现将 \(a_i,a_{i-1}\) 改成两者较小一定是更优的，因为这样后面的一些小数就可以花费较少的花费达到严格不降得目的。
↑上述问题其实也是我在学习的时候遇到的一个问题。
现在讨论完了两种情况，我们发现实际上我们只需要维护一个优先队列就可以完成快速维护关键点的工作。
而快速维护关键点实质上就是快速维护 \(F_i(x)\)，也就是快速得到 \(G_i(x)\)。
那么最后答案当然就是 \(F_n(h(n))\) 啦~
实际操作的时候我们不需要另外开一个 f[] 来存下所有的 \(G_i(\max(a_i,h(i-1))\)（对的，是这玩意），只需要一个 ans 算贡献就好，因为我们的全部过程只需要利用到 \(F_{i-1}\) 的相关信息。
代码如下：
/*
========= Plozia =========
Author:Plozia
Problem:CF713C Sonya and Problem Wihtout a Legend
Date:2021/9/22
========= Plozia =========
*/
#include <bits/stdc++.h>
using std::priority_queue;
typedef long long LL;
const int MAXN = 3000 + 5;
int n, a[MAXN];
LL ans = 0;
priority_queue <LL> q;
int Read()
{
int sum = 0, fh = 1; char ch = getchar();
for (; ch < '0' || ch > '9'; ch = getchar()) fh -= (ch == '-') << 1;
for (; ch >= '0' && ch <= '9'; ch = getchar()) sum = (sum * 10) + (ch ^ 48);
return sum * fh;
}
int Max(int fir, int sec) { return (fir > sec) ? fir : sec; }
int Min(int fir, int sec) { return (fir < sec) ? fir : sec; }
int main()
{
n = Read();
for (int i = 1; i <= n; ++i) a[i] = Read() - i;
for (int i = 1; i <= n; ++i)
{
q.push(a[i]);
if (q.top() > a[i])
{
ans += q.top() - a[i];
q.pop(); q.push(a[i]);
}
}
printf("%lld\n", ans);
return 0;
}
3. 总结
Slope Trick 通常解决的是这样一类问题：
- DP 中维护的 \(f\) 数据具有凸性。
- 可以通过维护关键点和最右端的一次函数来快速处理最大/最小值。
推荐练习题：P3642 [APIO2016]烟火表演。
