数据结构专题-学习笔记：莫队#2（带修莫队，树上莫队）

回顾：
3.练习题

回顾：

上回我们在数据结构专题-学习笔记：莫队#1（普通莫队）讲解了莫队的一般套路以及各种优化方式，但那只是基础，接下来将会介绍莫队更多的用法。这篇博文将会讲述带修莫队、树上莫队、树上带修莫队的用法，在数据结构专题-学习笔记：莫队#3（回滚莫队，莫队二次离线）中将会讲述回滚莫队/不删除莫队、莫队二次离线/第十四分块（前体）的思路以及实现。同时总结将会写在数据结构专题-学习笔记：莫队#3（回滚莫队，莫队二次离线）当中。

3.练习题

题单：

普通练手题

这里的题目都比较简单，因此代码就少贴一点。只需要更改 del&add 函数即可。主函数几乎不需要改。

CF220B Little Elephant and Array

首先可以发现，\(a_i>n\) 的数据完全没有用，因此 \(cnt\) 统计 \(a_i<n\) 的数据即可。

其次需要注意，只有 \(cnt_{a_i}=a_i\) 的数据是有效数据，大于或小于都不行

知道了这些，就跟例题没什么两样了（见莫队算法总结&专题训练1）。

贴一下 del&add 函数：

void del(int x)
{
	if(a[x]>n) return ;
	if(cnt[a[x]]==a[x]) total--;
	cnt[a[x]]--;
	if(cnt[a[x]]==a[x]) total++;
}
void add(int x)
{
	if(a[x]>n) return ;
	if(cnt[a[x]]==a[x]) total--;
	cnt[a[x]]++;
	if(cnt[a[x]]==a[x]) total++;
}

P2709 小 B 的询问

简直模板。

当然这道题到目前为止没有 \(\log\) 级别的做法。

更新答案时有两种操作，一种手推公式更新，一种直接暴力先减掉 \(cnt_x^2\) 处理完之后再加回去，我采用的是第二种。

贴一下 del&add 函数：

void Delete(int x)
{
	sum-=cnt[a[x]]*cnt[a[x]];
	cnt[a[x]]--;
	sum+=cnt[a[x]]*cnt[a[x]];
}
void Add(int x)
{
	sum-=cnt[a[x]]*cnt[a[x]];
	cnt[a[x]]++;
	sum+=cnt[a[x]]*cnt[a[x]];
}

P1494 [国家集训队]小 Z 的袜子

这道题需要手推一下公式。

假设颜色为 \(a,b,c\) 的数据分别出现了 \(x,y,z\) 次，那么答案：

\(\dfrac{\frac{x \times (x-1)}{2} + \frac{y \times (y-1)}{2} + \frac{z \times (z-1)}{2} +...}{\frac{(r-l) \times (r-l+1)}{2}}\)

\(= \dfrac{x^2+y^2+z^2+......-(x+y+z+...)}{(r-l) \times (r-l+1)}\)

\(=\dfrac{x^2+y^2+z^2+......-(r-l+1)}{(r-l) \times (r-l+1)}\)

所以我们只需要维护平方和就好。代码不贴了。

需要注意：

不要忘记约分。
道路千万条，long long 第一条。乘积存 int ，爆零两行泪。

带修莫队

这里我们将接触莫队的第一个变种：带修莫队。

在上一个博文中，我说过一般的莫队是不能支持在线的，但是对于一部分修改，莫队还是能够承受的。

最典型的题目：P1903 [国家集训队]数颜色 / 维护队列

这道题的询问简直就是太水了呀！但是修改却使得莫队不能简单实现。

我们想一想，当初我们是怎么解决莫队的优化二的？两个指针 \(l,r\) 移来移去。那么究其原因，到底为什么我们要用两个指针 \(l,r\) 呢？难道只是从尺取法上得到的启发吗？

不仅仅是尺取法！我们使用 \(l,r\) 的很重要的原因就是因为他的询问是二维的（指区间是 \([l,r]\) 是二维的），可以使用两个指针操作！

那么这里，我们可以将修改看作多出来的一维时间，区间变成了 \([l,r,t]\) 三维，要解决它我们直接再弄一维时间 \(t\) 上去，让第三个指针 \(t\) 在时间轴上移来移去不就好了？

这就是带修莫队的主要思路：使用第三个指针 \(t\) 在时间轴上动，将两个修改之间的所有询问操作看成一个时间上的（包括这些询问操作之前的第一个修改操作也是同一个时间点），这样移动的时候将在区间里面的数和答案更新一下，同时处理修改即可。

这里的排序也需要注意：第一关键字是左端点所在的块，第二关键字是右端点所在的块，第三关键字是时间。

关于时间复杂度：可以证明，对于 \(k\) 个指针的莫队，最优块长 \(n^{\frac{k-1}{k}}\)，复杂度为 \(O(n^{1+\frac{k-1}{k}})\)，但是我不会证（

放代码：

#include<bits/stdc++.h>
using namespace std;

const int MAXN=133333+10,MAXA=1e6+10;
int n,m,a[MAXN],cnt[MAXA],total,ans[MAXN],cntq,cntc,size,block,ys[MAXN<<1];
struct query
{
    int l,r,id,Time;
}q[MAXN];
struct change
{
    int pos,val;
}c[MAXN];

int read()
{
    int sum=0;char ch=getchar();
    while(ch<'0'||ch>'9') ch=getchar();
    while(ch>='0'&&ch<='9') {sum=(sum<<3)+(sum<<1)+(ch^48);ch=getchar();}
    return sum;
}
void print(int x,char tail=0)
{
    if(x>9) print(x/10);
    putchar(x%10+48);
    if(tail) putchar(tail);
}

bool cmp(const query &fir,const query &sec)
{
    if(ys[fir.l]^ys[sec.l]) return ys[fir.l]<ys[sec.l];
    if(ys[fir.r]^ys[sec.r]) return ys[fir.r]<ys[sec.r];//再次提醒，第二关键字是右端点所在的块而不是右端点！
    return fir.Time<sec.Time;
}

int main()
{
    n=read();m=read();size=2000;//手动调块长qwq
    for(int i=1;i<=n;++i) ys[i]=(i-1)/size+1;
    for(int i=1;i<=n;++i) a[i]=read();
    for(int i=1;i<=m;++i)
    {
        char ch=getchar();
        while(ch==' '||ch=='\n'||ch=='\r') ch=getchar();
        if(ch=='Q')
        {
            q[++cntq].l=read();
            q[cntq].r=read();
            q[cntq].id=cntq;
            q[cntq].Time=cntc;//处理时间
        }
        else
        {
            c[++cntc].pos=read();
            c[cntc].val=read();
        }//保存修改操作
    }
    sort(q+1,q+cntq+1,cmp);
    int l=1,r=0,t=0;
    for(int i=1;i<=cntq;++i)
    {
        while(l<q[i].l) total-=!--cnt[a[l++]];
        while(l>q[i].l) total+=!cnt[a[--l]]++;
        while(r<q[i].r) total+=!cnt[a[++r]]++;
        while(r>q[i].r) total-=!--cnt[a[r--]];
        while(t<q[i].Time)
        {
            ++t;
            if(q[i].l<=c[t].pos&&c[t].pos<=q[i].r) total-=!--cnt[a[c[t].pos]]-!cnt[c[t].val]++;
            swap(a[c[t].pos],c[t].val);
        }
        while(t>q[i].Time)
        {
            if(q[i].l<=c[t].pos&&c[t].pos<=q[i].r) total-=!--cnt[a[c[t].pos]]-!cnt[c[t].val]++;
            swap(a[c[t].pos],c[t].val);
            --t;
        }
        ans[q[i].id]=total;
    }
    for(int i=1;i<=cntq;++i) print(ans[i],'\n');
    return 0;
}

总结一下：

对于带修莫队这种二维变三维的东西，最简单的方法就是新开一个变量/数组/数据结构维护。比如带修莫队就是使用了第三个指针 \(t\) 来维护时间轴。

树上莫队

到目前为止所碰到的莫队，都是在序列上操作的。既然莫队如此万能（雾），那么我们能不能够让莫队去树上玩一玩呢？

答案是肯定的。不要认为这个东西很难，实际上还是一个序列。

前置知识：求最近公共祖先（lca），任何一种方法都可以。

作者使用的是倍增算法求 lca 。

SP10707 COT2 - Count on a tree II

由于莫队只能够在序列上操作，因此我们首先就要想办法将树变成一个序列。最容易想到的当然是 DFS序。

比如下面这棵树：

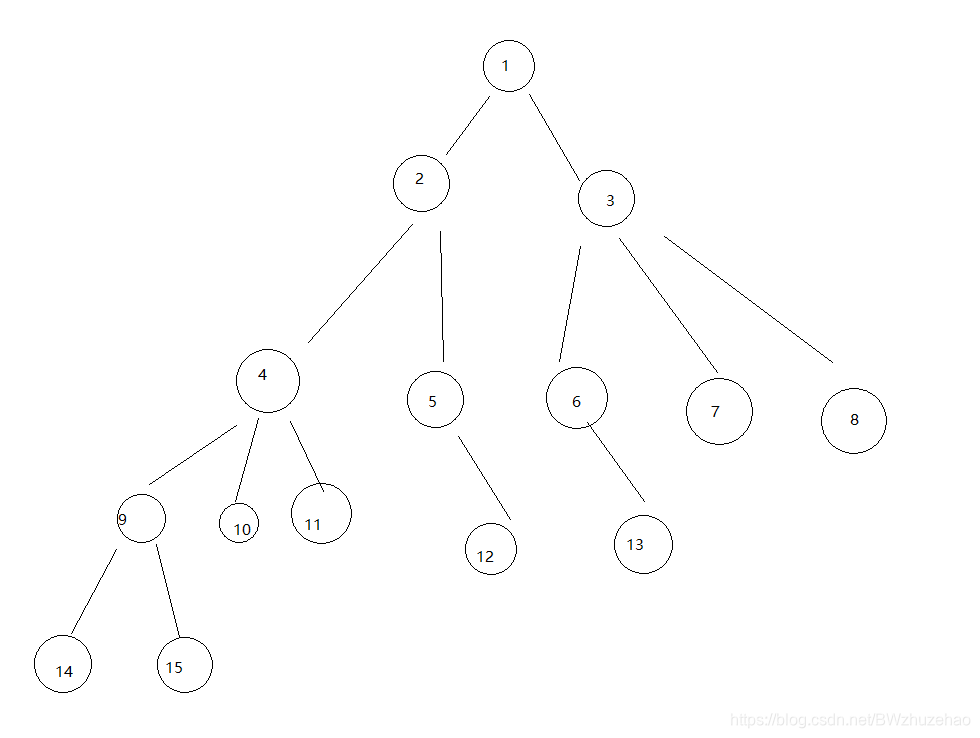
在这里插入图片描述

DFS序：1 2 4 9 14 15 10 11 5 12 3 6 13 7 8
4->13上的节点：4 2 1 3 6 13
在 DFS序上对应的区间：唉等等，区间呢？

这里，我可以很负责任的告诉你：普通的 DFS序搞不了树上莫队。

那么还有没有什么办法呢？

有！不要忘记我们还有 欧拉序 这一利器。

首先跑一遍欧拉序：

1 2 4 9 14 14 15 15 9 10 10 11 11 4 5 12 12 5 2 3 6 13 13 6 7 7 8 8 3 1

关于欧拉序的求法可以自行百度（不过应该都看出来了），那么它为什么能够将树上莫队转换成区间莫队呢？

假设我们要找 1->10 上的节点：1 2 4 10

把欧拉序上 1->10 的区间拿出来······等等，有两个 1，那么拿哪一个呢？

这里，我们统一取前面的 1 。为了方便，接下来令 \(fir_i\) 表示 \(i\) 节点在欧拉序中第一次出现的位置，\(las_i\) 表示 \(i\) 节点在欧拉序中第二次出现的位置。

那么我们把 \(fir_1,fir_{10}\) 的区间拉出来：1 2 4 9 14 14 15 15 9 10

也不对啊，这里面还是有 9,14,15 等干扰数据啊，这方法是不是不靠谱啊？

但是不要忘记在讲优化二的时候我提到过：莫队处理答案时先加一个数在删一个数是对答案没有影响的。

所以我们可以用一个 \(vis\) 数组来记录当前节点有没有被访问过，访问过就删，否则就加。这样，删除了出现两次的数据， \([fir_1,fir_{10}]\) 就等价于 1 2 4 10。

然而这样做有个问题。

比如我们要查找 4->13 对应的节点：4 2 1 3 6 13

把 \([fir_4,fir_{13}]\) 拉出来：4 9 14 14 15 9 10 10 11 11 4 5 12 12 5 2 3 6 13

删除重复元素······4呢？怎么删没了？

这就是问题 1：我们很容易在操作的时候把 4 干掉了，这样答案就会不正确。

处理方法：使用 \([las_4,fir_{13}]\) 的区间。这样，就可以避免删除 4。

但是上面又说使用 \([fir,fir]\) 区间，那么什么时候用 \(las\) ，什么时候用 \(fir\) 呢？

不急，先把 \([las_4,fir_{13}]\) 拉出来：4 5 12 12 5 2 3 6 13

删除公共元素：4 2 3 6 13。等等， 1 呢？ 1 是 \(lca(4,13)\) 啊！

那么我们在处理的时候还要加上 \(lca(4,13)\) 。但是因为 \(lca(4,13)\) 不在区间内，那么在算完答案之后还要删掉。

那么解答前面的问题：什么时候用 \([fir,fir]\) ，什么时候用 \([las,fir]\) 呢？

这也就是树上莫队对询问的处理：

首先假设询问 \(x->y\) ，那么算一下 \(lca(x,y)\) 。为了方便，我们规定 \(fir_x<fir_y\) ，不满足就交换。
然后，如果 \(lca(x,y)=x\) 那么使用 \([fir_x,fir_y]\) ，因为此时 \(x,y\) 在一条链上。否则，使用 \([las_x,fir_y]\) ，同时记录 \(lca(x,y)\) 。

在处理询问时要注意两个点：

若 \(x,y\) 在一条链上，不要处理 \(lca\) ，否则要处理 \(lca\) 。
\(lca\) 需要处理两次（因为不在区间内）

几个坑点（重点）：

欧拉序长度是 \(2n\) ，千万不能在这里 TLE 了！
块长调 \((2n)^{\frac{2}{3}}\)。
针对这个题不要忘记离散化。

上代码：

#include<bits/stdc++.h>
using namespace std;

const int MAXN=4e5+10;
int n,m,cnt[MAXN],eular[MAXN<<1],cnte,ans[MAXN],total,ys[MAXN<<1],block,fa[MAXN][21],dep[MAXN],a[MAXN],fir[MAXN],las[MAXN],vis[MAXN],b[MAXN],lastn;
struct node
{
	int l,r,id,lca;
}q[MAXN];
vector<int>Next[MAXN];

int read()
{
	int sum=0;char ch=getchar();
	while(ch<'0'||ch>'9') ch=getchar();
	while(ch>='0'&&ch<='9') {sum=(sum<<3)+(sum<<1)+(ch^48);ch=getchar();}
	return sum;
}

void dfs(int x)
{
	eular[++cnte]=x;
	fir[x]=cnte;
	for(int i=0;i<Next[x].size();i++)
	{
		int u=Next[x][i];
		if(dep[u]) continue;
		dep[u]=dep[x]+1;
		fa[u][0]=x;
		dfs(u);
	}
	eular[++cnte]=x;
	las[x]=cnte;
}

void st()
{
	for(int j=1;j<=20;j++)
		for(int i=1;i<=n;i++)
			fa[i][j]=fa[fa[i][j-1]][j-1];
}


int getlca(int x,int y)
{
	if(dep[x]<dep[y]) swap(x,y);
	for(int j=20;j>=0;j--) if(dep[x]>=dep[y]) x=fa[x][j];
	if(x==y) return x;
	for(int j=20;j>=0;j--) if(fa[x][j]!=fa[y][j]) x=fa[x][j],y=fa[y][j];
	return fa[x][0];
}

bool cmp(const node &fir,const node &sec)
{
	if(ys[fir.l]^ys[sec.l]) return ys[fir.l]<ys[sec.l];
	if(ys[fir.l]&1) return fir.r<sec.r;
	return fir.r>sec.r;
}

void del(int x)
{
	int t=lower_bound(b+1,b+lastn+1,a[x])-b-1;
	total-=!--cnt[t];
}
void add(int x)
{
	int t=lower_bound(b+1,b+lastn+1,a[x])-b-1;
	total+=!cnt[t]++;
}
void work(int pos)
{
	vis[pos]?del(pos):add(pos);vis[pos]^=1;
}

int main()
{
	n=read();m=read();
	for(int i=1;i<=n;i++) b[i]=a[i]=read();
	sort(b+1,b+n+1);
	lastn=unique(b+1,b+n+1)-b-1;
	for(int i=1;i<n;i++)
	{
		int x=read(),y=read();
		Next[x].push_back(y);
		Next[y].push_back(x);
	}
	fa[1][0]=1;dep[1]=1;dfs(1);st();
	block=ceil(sqrt(cnte));
	for(int i=1;i<=(n<<1);i++) ys[i]=(i-1)/block+1;
	for(int i=1;i<=m;i++)
	{
		int x=read(),y=read(),lca=getlca(x,y);q[i].id=i;
		if(fir[x]>fir[y]) swap(x,y);
		if(fir[x]==lca) q[i].l=fir[x],q[i].r=fir[y];
		else q[i].l=las[x],q[i].r=fir[y],q[i].lca=lca;
	}
	sort(q+1,q+m+1,cmp);
	int l=1,r=0;
	for(int i=1;i<=m;i++)
	{
		while(l<q[i].l) work(eular[l++]);
		while(l>q[i].l) work(eular[--l]);
		while(r<q[i].r) work(eular[++r]);
		while(r>q[i].r) work(eular[r--]);
		if(q[i].lca) work(q[i].lca);
		ans[q[i].id]=total;
		if(q[i].lca) work(q[i].lca);
	}
	for(int i=1;i<=m;i++) printf("%d\n",ans[i]);
	return 0;
}

树上带修莫队

树上带修莫队，顾名思义，就是将树上莫队和带修莫队结合在一起的莫队。

因此只要你掌握了树上莫队和带修莫队，那么树上带修莫队简直就是轻而易举！

具体的思路如下：

首先按照树上莫队思路跑一遍欧拉序，处理操作。
处理操作时如果是询问操作那么按照树上莫队处理；同时根据带修莫队的处理方式，不要忘记处理修改和时间轴。
搞三个指针 \(l,r,t\) 处理即可。

P4074 [WC2013]糖果公园

思路与实现参见这篇文章->link

那么到目前位置，我们已经讲完了普通莫队、带修莫队、树上莫队、树上带修莫队四种莫队，在数据结构专题-学习笔记：莫队#3（回滚莫队，莫队二次离线）中，将会讲解最后两种莫队：回滚莫队/不删除莫队，莫队二次离线/第十四分块（前体），同时将会总结长达三篇博文的莫队讲解。

posted @ 2022-04-13 21:33 Plozia 阅读(109) 评论(0) 编辑收藏举报

刷新页面返回顶部

Plozia的博客

——一名普通的 ZJ OIer~