递归 是算法竞赛比较基础的一种思想，由于其时间复杂度[1]普遍较高，且适应用广，通常把它归类为 朴素算法 ，即 暴力算法 ，对其哪怕只是有了解也会对今后学习有帮助。
  本文会通过对递归问题的解析让读者理解递归问题，但由于个人知识有限，可能会有纰漏，若发现请指正。

一. 递归概述

  所谓递归，就是通过一定的规则，把大问题化为小问题，再把小问题化为更小的问题，最终化为可以求解的问题的一种思想。
用数学的话来说，可以表达为

\[a_n = f( a_1, a_2 ,\ ... \ ,a_{n - 1} ) \]

  \(a_n\) 就是我们要求解的问题，\(f\) 是一种运算法则，可以通过一定的规则得出一个数。

  对于初学者可能有点抽象，举个例子，小学就学过等差数列，可以表示为

\[\begin{equation} \begin{split} a_0 &= 0 \\ a_n &= a_{n - 1}+4 \end{split} \end{equation} \tag{1} \]

  其中 \(a_{n - 1}+4\) 就是 \(f\)，自变量为 \(a_{n - 1}\)，通过计算可以得出，此数列为 \(0\ 4\ 8\ 12\ 16\ 20\ ...\)

  现在，假如我们要求解 \(a_{100}\)，就需要知道 \(a_{99}\)；而要知道 \(a_{99}\)，就要知道 \(a_{98}\)，以此类推，最后到 \(a_0\)，这就是 递。
  找到了 \(a_0\) 这个已知的值，就可以通过 \(a_n = a_{n - 1}+4\) 进行运算，求出 \(a_1,a_2,a_3,...,a_{99}\)，最后就不难求出 \(a_{100}\)的值，这就是 归。

  上面的 式(1) 就是 递归式。

二. 汉诺塔

  好了，你现在已经具备了基础知识，我们来看一些例题吧，我们会在题目中继续学习。

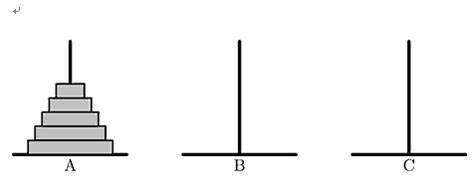
  这是一个有名的递归问题，你常会在某些地方遇见它。

  题目如下

  如图，有三根柱子，分别标号为A、B、C，在柱子A上有若干个圆盘，从下到上由大到小排列。
  现在，你要将A上的圆盘全部移到C上去，但是，你力气太小，一次只能移动一个圆盘，且由于大的圆盘会把小圆盘压坏，大圆盘不能在小圆盘上面。
  请问，移动的最少步数是多少？

  有一个与此相关的传说

  在世界中心贝拿勒斯（在印度北部）的圣庙里，一块黄铜板上插着三根宝石针。印度教的主神梵天在创造世界的时候，在其中一根针上从下到上地穿好了由大到小的64片金片，这就是所谓的汉诺塔。不论白天黑夜，总有一个僧侣在按照下面的法则移动这些金片：一次只移动一片，不管在哪根针上，小片必须在大片上面。僧侣们预言，当所有的金片都从梵天穿好的那根针上移到另外一根针上时，世界就将在一声霹雳中消灭，而梵塔、庙宇和众生也都将同归于尽。

  当我们学习完这一部分时，我们会知道这时间有多么长。

  先来观察一下 小的情形，这是通向成功的重要途径。

  设 \(H_n\) 为有 \(n\) 个圆盘时的最小移动步数
  当 \(n = 0 \) 时，由于没有圆盘可以移动，有 \(H_1 = 1\)， 即 \(A \rightarrow C\)。
  当 \(n = 1 \) 时，明显有 \(H_1 = 1\)， 即 \(A \rightarrow C\)。
  当 \(n = 2 \) 时，有 \(H_2 = 3\)，即\(A \rightarrow B，A \rightarrow C，B \rightarrow C，\)
  以此类推，可得下表

\[\begin{array}{|c|c|c|c|c|c|} \hline n & 1 & 2 & 3 & 4 & \cdots \\ \hline H_{n} & 1 & 3 & 7 & 15 & \cdots \\ \hline \end{array} \]

  看起来有

\[\begin{align*} H_0 &= 0 \\ H_n &= 2H_{n - 1} + 1 \end{align*} \]

  我们来看看为什么会这样

  要在 \(A\) 柱上移走 \(n\) 个圆盘，首先要移走在第 \(n\) 个圆盘上的 \(n - 1\) 个圆盘，由于第 \(n\) 个圆盘是最大的，所以对其余的 \(n - 1\) 个圆盘的移动不造成影响，所以问题就分解为移动第 \(n\) 个圆盘与移动上面的 \(n - 1\) 个圆盘。

  • 第一步，将 \(n - 1\) 个圆盘从 \(A\) 柱移动到 \(B\) 柱上
  • 第二步，将第 \(n\) 个圆盘从 \(A\) 柱移动到 \(C\) 柱上
  • 第三步，将 \(n - 1\) 个圆盘从 \(B\) 柱移动到 \(C\) 柱上

  所以我们可以知道

\[\begin{equation} \begin{split} H_n \leqslant 2H_{n - 1} + 1 \end{split} \end{equation} \tag{2} \]

  之所以要用 \(\leqslant\) 而不是 \(=\) ，是因为我们只是知道了众多方法中的一种，并不能说明它的每一步是必须的，所以不能确定这个步数是最小的。
  那么，有更好的方法吗？仔细思考一下，你会发现实际上没有。
  迟早你都要移动第 \(n\) 个圆盘，但是，要移动第 \(n\) 个圆盘，就必须要移动位于第 \(n\) 个圆盘上的 \(n - 1\) 个圆盘。你的目标是把 \(n\) 个圆盘从 \(A\) 柱移动到 \(C\) 柱上，所以，你只能把 \(n - 1\) 个圆盘从 \(A\) 柱移动到 \(B\) 柱上，等到第 \(n\) 个圆盘移动完毕后在径直从 \(B\) 柱移动到 \(C\) 柱上。所以我们有

\[\begin{equation} \begin{split} H_n \geqslant 2H_{n - 1} + 1 \end{split} \end{equation} \tag{3} \]

  结合 \(式(2)\) 与 \(式(3)\) 容易得到

\[H_n = 2H_{n - 1} + 1 \]

  好了上式就是我们要的答案了。
  整理一下，长这样

\[\begin{equation} \begin{split} H_0 &= 0 \\ H_n &= 2H_{n - 1} + 1 \end{split} \end{equation} \tag{4} \]

  挺漂亮的。

  但是有一个问题，如果你需要计算 \(H_{10}\) 还好说，可以通过暴力代值解决，但是如果要计算如之前问题中的 \(H_{64}\) 甚至于 \(H_{10000}\) ，直接代值对于人类来说肯定不现实，所以，要成为超人的存在才行，我不做人啦！！！！！要找到一种能方便计算的形式，及 封闭形式，此式只与 \(n\) 有关。

  关于封闭形式，举个例子来说前面的等差数列，递归式长这样

\[\begin{align*} a_0 &= 0 \\ a_n &= a_{n - 1}+4 \end{align*} \]

  而它的封闭形式则长这样

\[H_n = 4n \]

  可以在一次找到 \(H_n\) 的值，而不需要再去找 \(H_{n - 1}\) 的值，这就是封闭形式。

  回到汉诺塔问题上来，我们还是首先观察一下这些数据有什么特点，只是上一次是用递归式表达，这一次我们用封闭形式来表达。

\[\begin{array}{|c|c|c|c|c|c|} \hline n & 1 & 2 & 3 & 4 & \cdots \\ \hline H_{n} & 1 & 3 & 7 & 15 & \cdots \\ \hline \end{array} \]

  用封闭形式来说，好像有

\[\begin{equation} \begin{split} H_n = 2^n - 1 \end{split} \end{equation} \tag{5} \]

  我们将其代回 \(式(4)\)

\[\begin{align*} H_n &= 2H_{n-1} + 1 \\ 2^n - 1 &= 2(2^{n - 1} - 1) + 1 \\ 2^n - 1 &= 2^n - 2 + 1\\ 2^n - 1 &= 2^n - 1 \end{align*} \]

  所以封闭形式 \(式(5)\) 对于递归式 \(式(2)\) 是成立的。
  这就是著名的 数学归纳法，\(H_1 = 1\) 称为 基础，而上述证明过程称为 归纳。
  以上的一切都建立在一个灵光的大脑上面，如果你没有这样一个令人羡慕的大脑，也有一种属于你的方法。
  我们可以对 \(式(2)\) 进行一些变形

\[\begin{align*} H_0 &= 0 \\ H_0 + 1 &= 1 \\ \\ H_n &= 2H_{n-1} + 1 \\ H_n + 1 &= 2H_{n-1} + 2 \end{align*} \]

  令 \(A_n = T_n + 1\)，可以得到

\[\begin{align*} A_0 &= 1 \\ A_n &= 2A_{n - 1} \end{align*} \]

  可以轻松知道

\[A_n = 2^n \]

  所以就有

\[H_n = 2^n - 1 \]

  艰辛的推理与证明终于结束了！

  现在我们来看一下最开始的问题，\(H_{64}\) 是多少呢？根据 \(式(5)\) 可以算出 \(H_{64} = 2^{64} - 1 = 18\ 446\ 744\ 073\ 709\ 551\ 615\),如果僧侣一秒移动一个的话，那么宇宙共有 \(584\ 942\ 417\ 355\) 年寿命，しかし，科学家预测的宇宙寿命只有 \(140\ 000\ 000\ 000\)年，相差甚远。

总结

  要求解一个递归问题，有如下步骤

  • 观察小的情形
  • 给出递归式并证明
  • 给出封闭形式并证明

  这样就能成功地解决一个递归问题了！

  1. 时间复杂度：其实可以理解为是程序执行次数的平均值，是评估程序运行时间的一大标准 ↩︎