【算法】单源最短路——Dijkstra

对于固定起点的最短路算法，我们称之为单源最短路算法。单源最短路算法很多，最常见的就是dijkstra算法。

dijkstra主要用的是一种贪心的思想，就是说如果i...s...t...j是最短路，那么i和j之间的任意两点s,t之间也一定是最短路，非常好证，如果s，t之间不是最短路，那么必然存在最短路，那么i到j也不是最短路造成了矛盾。

而dijkstra就是运用这样的思想，把起点首先放进一个集合S中，其他的点在另一个集合中，每次取起点经过集合S中的点可达的最短路的点，加入到集合S中，并且根据新加入的店刷新一遍最短路。直到所有的点都在集合S中。

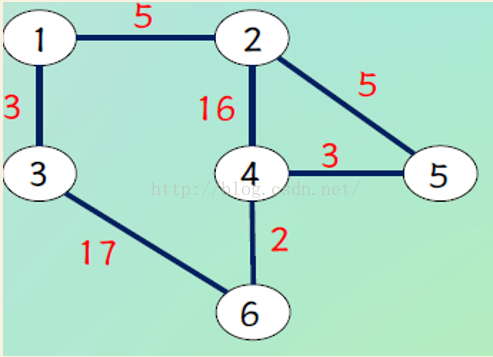
如上图，假设以1为起点，dis[i]为起点到i点的最短距离，如果没法直达则为INF

第一次：S中只有1，那么1能直达的点有2，3，取路径最短的3加入S，并更新一遍dis，发现6可达，dis[6] = 20；

第二次：S中有1，3，可达的有2，6，取2，则4，5可达，dis[4] = 21,dis[5] = 10；

第三次：S中有1，2，3，可达的有4，5，6，取5，到4多了新路径且比原来近，更新dis[4] = 13；

第四次：S中有1，2，3，5，可达的有4，6，取4，到6多了新路径且比原来近，更新dis[6] = 15；

第五次：S中有1，2，3，4，5，可达的有6，只有6不在S中，取6，不更新，完成算法

 

要注意的是外围循环是除了起点外的点数，如果多一次，pos会无法赋值因为所有的点都遍历过了，造成变量没有初始化而程序崩溃。

代码如下：

 

[cpp] view plain copy
 
  1. #include <cstdio>  
  2. #include <algorithm>  
  3. #include <cstring>  
  4. using namespace std;  
  5. const int maxn = 10;  
  6. int map[maxn][maxn], dis[maxn];  
  7. int n;                                                         //点数  
  8.   
  9. void init()  
  10. {  
  11.     for (int i = 1; i <= n; i++)  
  12.         for (int j = 1; j <= n; j++)  
  13.             map[i][j] = 0x3f3f3f;  
  14.     memset(dis, 0, sizeof(dis));  
  15. }  
  16. void dijkstra(int v0)  
  17. {  
  18.     for (int i = 1; i <= n; i++)  
  19.         dis[i] = map[v0][i];  
  20.     map[v0][v0] = 0;  
  21.     for (int i = 1; i < n; i++)                                //注意循环的次数，如果到n，最后一次所有的map[i][i]都是0，pos找不到值会崩溃，如果初始化为0则dis[i]最后全是0（dis[0] = 0）  
  22.     {  
  23.         int min_dis = 0x3f3f3f3f,pos;  
  24.         for (int j =1; j <= n; j++)  
  25.         {  
  26.             if (map[j][j] && dis[j] < min_dis)                 //遍历所有点找到距离v0最小的点，记录下距离，并将其加入已计算的集合，将其编号用pos记录下来  
  27.                 min_dis = dis[pos = j];  
  28.         }  
  29.         map[pos][pos] = 0;                                     //用map[i][i]来表示某个点是否被访问过，节省空间  
  30.   
  31.         for (int j = 1; j <= n; j++)  
  32.         {  
  33.             dis[j] = min(dis[j], dis[pos] + map[pos][j]);      //用新添加的点来更新一边dis  
  34.         }  
  35.     }  
  36. }  
  37.   
  38. int main()  
  39. {  
  40.     freopen("input.txt", "r", stdin);  
  41.     int m,u,v,w,target;  
  42.     scanf("%d%d", &n,&m);  
  43.     init();  
  44.     while (m--)  
  45.     {  
  46.         scanf("%d%d%d", &u, &v, &w);  
  47.         map[u][v] = map[v][u] = w;  
  48.     }  
  49.     scanf("%d", &target);  
  50.     dijkstra(target);  
  51.     for (int i = 1; i <= n; i++)  
  52.     {  
  53.         printf("%d : %d\n", i, dis[i]);  
  54.     }  
  55.     return 0;  
  56. }  

但要注意的是，dijkstra不能计算含有负权的图的最短路，因为一直加负数始终会比原来的小。

 posted on 2018-04-24 10:05  做个快乐的自己  阅读(510)  评论(0)  编辑  收藏  举报