IOI 2020 集训队作业胡扯「101, 150」
IOI 2020 集训队作业胡扯「1, 50」
IOI 2020 集训队作业胡扯「51, 100」
IOI 2020 集训队作业胡扯「101, 150」（★）
如果您点击了某个超链接，但是并没有发生任何变化，这意味着您可能需要在另外两章节中寻找对应内容。
表格
绿的表示主要没看题解，红的表示主要看了题解。
2020-02-29
agc028_d
令 \(n = 2N\)。
把圆上看成序列上也可以，也就是说如果 \([l_1, r_1]\) 和 \([l_2, r_2]\) 相交但不包含，那么转化到圆上他们就是相交的。
考虑对于每个连通块，计算它对答案的贡献次数，加起来就是答案。
我们发现一个连通块在序列上一定对应了恰好一个区间，满足连通块完全在这个区间内，而且区间端点属于连通块。
但是要注意并不是这个区间内全都是这个连通块，可能其中还有小连通块。
则令 \(dp(i, j)\) 表示区间 \([i, j]\) 内任意连边，且 \(i, j\) 在同一连通块内的区间内连边方案数。
枚举这个区间 \([i, j]\)，它的长度一定为偶数。则可以发现这个区间内的点不能向区间外连边，这是有利于统计的。
如果区间内任意连边，那么方案数就是 \(dp(i, j) = g(c(i, j))\)。
其中 \(g(x)\) 表示 \(x\) 个点的环任意连边的方案数，当 \(x\) 为偶数时等于 \(1 \cdot 3 \cdot 5 \cdot \cdots \cdot (x - 1)\)，否则为 \(0\)。
而 \(c(i, j)\) 为 \([i, j]\) 内还没确定连边情况的点的个数。
但是还有第二个条件，就是 \(i, j\) 在同一个连通块内。考虑容斥，如果不在，枚举 \(i\) 连通块的区间右端点 \(k\)。
有 \(\displaystyle dp(i, j) = g(c(i, j)) - \sum_{k = i}^{j - 1} dp(i, k) \cdot g(c(k + 1, j))\)。
最后求出所有 \(dp(i, j)\) 后，就有答案等于 \(\displaystyle \sum dp(i, j) \cdot g(n - 2K - c(i, j))\)。
时间复杂度为 \(\mathcal O (n^3)\)，评测链接。
2020-03-01
agc029_f
可以发现，选择一部分给定的 \(E_i\)，即选出 \(\mathcal{E} = \{E_1, E_2, \ldots , E_{N - 1}\}\) 的一个子集 \(\mathcal{S} \subseteq \mathcal{E}\)。
考虑 \(\mathcal{S}\) 能够连通的所有点，令它们为 \(f(\mathcal{S})\)，即 \(f(\mathcal{S}) = \{u \mid u \in E_i \in \mathcal{S}\}\)。
如果 \(\mathcal{S}\) 非空且 \(|f(\mathcal{S})| \le |\mathcal{S}|\)，那就完蛋了，因为不管怎么使用这 \(|\mathcal{S}|\) 条边，都会连出环来，造不成树。
也就是说，对于任意 \(\mathcal{S} \ne \varnothing\)，都必须要有 \(|f(\mathcal{S})| \ge \mathcal{S} + 1\)。
这是一个有解的必要条件，之后的构造显示了它也是充分条件。
看起来很 Hall 定理，先整个二分图匹配再说吧。
二分图左边为 \(N\) 个点，右边为 \((N - 1)\) 个点集，如果 \(u \in E_i\)，则左边的 \(u\) 对应的点与右边的 \(E_i\) 对应的点之间连边。
这样必须要有右侧的 \((N - 1)\) 个点的完备匹配，如果求不出来一定无解，可以使用 Dinic 实现。
那么左边就会有恰好 \(1\) 个点没被匹配到，令它为 \(r\)。
考虑从 \(r\) 开始 DFS，随便找到一个与 \(r\) 相邻的，且未被经过的右侧的点 \(i\)，把它标记为被经过了，令这个点在左侧的匹配为 \(u\)，然后就能确定 \(E_i\) 中选择的两个点是 \(r\) 和 \(u\)。然后 DFS 递归进 \(u\)，这样一直下去直到把所有点都经过为止。
如果还没有经过所有点，就无法拓展新点而返回了，那就是无解。
这个过程有没有可能把有解判成无解呢？
如果过程中途停止了的话，当且仅当：对于所有的左侧被经过的点，与它们相邻的右侧的点都被经过了，无法拓展新点。
显然左侧被经过的点数在任意时刻都等于右侧被经过的点数 \(+ 1\)，因为多了一个 \(r\)。
考虑令 \(\mathcal{S}\) 为右侧未被经过的点，它们在左侧对应的点也是未被经过的，那么 \(|f(\mathcal{S})| \le |\mathcal{S}|\)，也就是无解，与假设矛盾。
所以一定不会把有解判成无解，如果无解一定是 \(f(\mathcal{S})| \le |\mathcal{S}|\) 的情况出现了。所以 \(|f(\mathcal{S})| \ge \mathcal{S} + 1\) 是充分必要条件。
时间复杂度为 \(\mathcal O (N + M \sqrt{N})\)，评测链接。
2020-03-03
cf674G
如果 \(p = 50 + \varepsilon\) 会怎么样？
这便是一个经典问题：长度为 \(n\) 的数列中存在一个出现次数大于 \(n / 2\) 的数，设计一个算法找到它。
只要每次删除两个不同的数，最后留下的那个数（或那些数，但这些数全部相同）就是要求的答案。
原理是，如果一个数出现了 \(a\) 次，其中 \(a > n - a\)，则两边都减去 \(1\)，仍有 \(a - 1 > n - a - 1 = (n - 2) - (a - 1)\)。
对于拓展情况我们如法炮制，令 \(\displaystyle k = \left\lfloor \frac{100}{p} \right\rfloor\)。每次删除 \(k + 1\) 个数，则对的数一定会留下来。
因为 \(k\) 最大就是 \(5\)，建立一棵线段树，使用每次 \(\mathcal O (k^2)\) 的时间合并区间，不难维护答案。
时间复杂度为 \(\mathcal O (n k^2 \log n)\)，评测链接。
2020-03-04
agc030_f
也就是这 \(2 N\) 个数两两配对，然后每一对中的较小数会进到 \(B\) 里面去。
把已经确定有配对的（\(A_{2 i - 1}, A_{2 i} \ne -1\)）扔了，剩下的是一对里面已经有一个确定了的，和两个都没确定的。
我们把 \(1 \sim 2 N\) 排成一排，配对的连一条线，那么：
\(B\) 中的元素就是每条线的左端点的值，但是 \(B\) 里还有顺序，这该怎么办呢？
考虑：如果一条线的某一端的值，在 \(A\) 中是存在的，也就是说这一对的一端已经是确定的，那么在 \(B\) 中的位置也是确定的。
如果这条线两端的值都没有在 \(A\) 中，那么我们先不给这条线赋值，等到最后统计完所有方案后，可以发现这样的线的个数是确定的（就等于 \(N\) 减去一端在 \(A\) 中的数对的数量），假设为 \(S\)，把答案乘以 \(S!\) 就行了。
那么，也就是说，我们需要统计连线方案数，两个方案不同当且仅当某个位置在其中一个方案中是线的左端点，而在另一个方案中不是，或者某个左端点所在的线的标号不同（如果这条线的一端在 \(A\) 中存在）。
记 \(v_i\) 表示值 \(i\) 是否在 \(A\) 中存在。
则考虑从大往小 DP，设状态 \(dp(i, j, k)\) 表示已经考虑了 \(\ge i\) 的数值，其中有 \(j\) 个 \(v_x = 0\) 的右端点 \(x\) 还没配对，其中有 \(k\) 个 \(v_x = 1\) 的右端点 \(x\) 还没配对。
可以发现 \(v_x = 0\) 的可以匹配 \(v_y = 0\) 或者 \(1\) 的，但是 \(v_x = 1\) 的只能匹配 \(v_y = 0\) 的。
则有转移：\(dp(i + 1, j, k)\) 可以转移给：
- \(v_i = 1\)：\(dp(i, j - 1, k)\)，系数为 \(1\)；表示匹配了更大的一个 \(v_x = 0\) 的。
- \(v_i = 1\)：\(dp(i, j, k + 1)\)，系数为 \(1\)；表示要向更小的值匹配。
- \(v_i = 0\)：\(dp(i, j - 1, k)\)，系数为 \(1\)；表示匹配了更大的一个 \(v_x = 0\) 的。
- \(v_i = 0\)：\(dp(i, j, k - 1)\)，系数为 \(k\)；表示匹配了更大的一个 \(v_x = 1\) 的，注意这里要乘以 \(k\) 因为可以任选一个，且每一个带来的这条线的标号都不同。
- \(v_i = 0\)：\(dp(i, j + 1, k)\)，系数为 \(1\)；表示要向更小的值匹配。
时间复杂度为 \(\mathcal O (N^3)\)，评测链接。
cf698D
我们单独对每个目标 \(i\) 考虑它是否能被射击到，然后求和即可得到答案。
考虑一个射击到目标 \(i\) 的顺序，它的最后一发子弹会击中目标，而之前的子弹都是在清理障碍。
设最后一发子弹是从射击点 \(j\) 射向目标 \(i\) 的，把路径上的障碍一一列出。
则枚举一个障碍 \(x\)，使用另一个射击点 \(y\) 把这个障碍击中。
则我们称从 \(y\) 射击击中障碍的“目的”是为了给 \(j \to i\) “清障”，然后连一条从 \(y\) 到 \(j\) 的有向边。
从 \(y\) 射向 \(x\) 的路径上可能还有障碍，这样下去把所有的“目的”链连出来。
容易发现“目的”关系连成了一棵 DAG（这是因为某一次“清障”可能会让两个或更多的未来的射击受益）。
但是如果我们为目标排个序，优先考虑优先级更大的目标，则这个 DAG 可以看成一棵有序树。
也就是说同一个节点下的子树，排在前面的子树可以影响排在后面的（前面的“清障”会对未来产生影响）。
那么我们枚举这棵树的 DFS 序，然后每次令 DFS 序的第一个数击中要求目标，然后递归考虑障碍即可。
递归层数最多为 \(k\) 层，所以时间复杂度为 \(\mathcal O (n \cdot k! \cdot k)\)。
要注意的是障碍的判断，如果用极角序排序的话要注意精度，我使用 double 和 atan2 被出题人卡精度了。
时间复杂度为 \(\mathcal O (n \cdot k! \cdot k)\)，评测链接。
2020-03-05
agc021_e
既然是对球的颜色序列计数，那么就只需要考虑，对于每一个颜色序列，判断它是否可行。
假设总共喂了 \(R\) 个红球和 \(B\) 个蓝球，满足 \(R + B = K\)。
首先考虑一只变色龙在什么情况下最终才会变成红色：
- 它吃的红球比蓝球多。
- 它吃的红球和蓝球一样多（且不为 \(0\) 个），但是吃的最后一个球是蓝球。
如果 \(R < B\)，也就是红球总数比蓝球少，那么显然无解。
如果 \(R \ge B + N\)，也就是红球比蓝球还多 \(N\) 个，可以直接让每只变色龙吃的红球都比蓝球多，一定有解。
否则 \(B \le R < B + N\)，就只能让一些变色龙吃的红球和蓝球一样多，另一些变色龙红球吃的更多一些。
对于一种方案，我们进行调整：
- 如果某一只变色龙吃的红球比蓝球多两个以上，可以拿出一个红球分配给别的变色龙。
这样调整之后，就一定是：一些变色龙吃的红球比蓝球多恰好一个，另一些一样多。
令 R 表示一个红球，B 表示一个蓝球。
也就是恰好有 \(R - B\) 只变色龙多吃一个 R，其它 \(N - (R - B)\) 只变色龙吃的一样多。
如果 \(R = B\)，也就是 \(R - B = 0\)，不存在多吃一个 R 的变色龙，那么考虑吃掉了最后一个球的变色龙，那么最后一个球必然是 B，那么去掉这个蓝球，就等价于 \((R, B - 1)\) 的情况。
那么现在就至少有一只变色龙多吃一个 R，对于吃的一样多的变色龙，可以再调整：
如果它吃的不是恰好两个球（RB），那么可以在最后一个字符前取出一个 R 和一个 B，分给多吃了一个 R 的变色龙。
那么现在就变成了，每只吃的红球和蓝球一样多的变色龙，吃球的顺序都是 RB，它们的个数为 \(N - (R - B)\)。
然后剩下的 \(R - B\) 只变色龙，就可以直接每只多吃一个 R 然后满足条件了。
综上所述：对于 \(B < R < B + N\) 的情况，满足条件当且仅当能够取出 \(N - (R - B)\) 对 RB（有顺序）的子序列。
这等价于：对于每个前缀，这个前缀中的蓝球比红球最多多 \(B - (N - (R - B)) = R - N\) 个。
（就是说这个前缀中无法参与匹配的蓝球数量不能超过 \(R - N\) 个）
换句话说，令 R 为 \(+1\)，B 为 \(-1\)，则任意一个前缀和都应该要大于等于 \(-(R - N)\)。
可以看成从 \((0, 0)\) 向右（R）或向上（B）走到 \((R, B)\)，但是不能到达直线 \(y = x + (R - N)\) 的严格上方。
这是一类经典的组合问题，类似于卡特兰数的计算方法（翻转第一次碰到直线上方的部分），可以得到答案：
枚举 \(R\)（\(B = K - R\)）计算组合数即可得到答案。
时间复杂度为 \(\mathcal O (K)\)，评测链接。
agc032_e
先把 \(a\) 从小到大排序，对于每一对 \((i, j)\)，把 \(i, j\) 用一条线连起来。
如果 \(a_i + a_j < M\)，则用蓝色线，如果 \(a_i + a_j \ge M\)，则用红色线。
那么我们可以证明，一定存在一种最优情况，满足：
- 存在一个分界点，使得它左右两侧没有匹配，也就是没有连线经过分界点。
- 只考虑分界点左侧，则最小的数和最大的数连线，第二小的数和第二大的数连线，以此类推。
- 分界点右侧也是一样，最小的和最大的连线。
- 分界点左侧的线的颜色都是蓝色，分界点右侧的线的颜色都是红色。
用图表示就是这样：
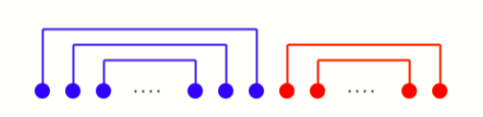
怎么证明它是对的呢？可以使用调整法。
考虑两个数对，如果它们同色但不包含，或者它们异色但不相离，则可以调整成满足条件且不更劣的情况。如图：
令四个数从左到右为 \(a, b, c, d\)，注意到 \(a \le b \le c \le d\)。
以及两个不等式：对于 \(x, y\)（\(x \le y\)），它们之间的线的权值 \(w\) 满足：
如果线是蓝色的，则 \(w \ge y\)；如果线是红色的，则 \(w < x\)。
反复使用这些不等式，即可得出调整后的情况不会更劣的结论。以右侧第三种情况为例：
- 令线 \(a \sim d\) 的权值为 \(x\)，线 \(b \sim c\) 的权值为 \(y\)。
- 因为 \(y \ge c \ge a > x\)，所以这种情况的权值较大值为 \(y\)。
- 考虑调整后的情况，因为线 \(b \sim c\) 变成了 \(b \sim a\)，而 \(a \le c\)，所以线还是蓝色的。
- 因为线 \(d \sim a\) 变成了 \(d \sim c\)，而 \(c \ge a\)，所以线还是红色的。
- 接下来证明权值较大值不会变得更大：
- 考虑线 \(a \sim b\)，其权值为 \(a + b \le b + c = y\)。
- 考虑线 \(c \sim d\)，其权值为 \(c + d - M < c \le b + c = y\)。
- 所以权值都不会变得更大，证毕。
其他情况的证明类似。
那么得到了这个结论后，如何计算答案呢？如果枚举分界点，然后计算答案是 \(\mathcal O (N^2)\) 的，不能接受。
我们弱化一下条件：每条线 \(x \sim y\) 都可以染蓝色，权值为 \(x + y\)，但是要染红色时必须有 \(x + y \ge M\)。
则可以发现：在满足条件的情况下，分界点越往左，答案越优，但是如果太往左了，就会导致分界点右侧不满足条件。
那么我们二分一下这个分界点即可。
时间复杂度为 \(\mathcal O (N \log N)\)，评测链接。
2020-03-07
cf671E
先定义两个数组 \(\mathrm{pre}[i]\) 和 \(\mathrm{suf}[i]\)：
\(\mathrm{pre}[i]\) 表示：从 \(1\) 出发到 \(i\) 需要花费多少单位的油（假设开始时油量充分大）。
\(\mathrm{suf}[i]\) 表示：从 \(i\) 出发到 \(1\) 需要花费多少单位的油（假设开始时油量充分大）。
则有 \(\mathrm{pre}[i] = \mathrm{pre}[i - 1] - g_{i - 1} + w_{i - 1}\)；
并且 \(\mathrm{suf}[i] = \mathrm{suf}[i - 1] - g_i + w_{i - 1}\)。
则从 \(i\) 向右走到 \(j\)，需要花费的油量就是 \(\mathrm{pre}[j] - \mathrm{pre}[i]\)。
则从 \(j\) 向左走到 \(i\)，需要花费的油量就是 \(\mathrm{suf}[j] - \mathrm{suf}[i]\)。
然后我们考虑去计算一个区间 \([l, r]\) 的代价 \(\boldsymbol{w(l, r)}\)：这个区间内需要给 \(\boldsymbol{g}\) 增加多少才可以往返通行。
如果 \(w(l, r) \le k\)，则这个区间就可以作为答案了。
先考虑从左往右开，从 \(l\) 一直开到 \(r\)，中间可能会遇到一个位置开不过去了，令这个位置为 \(\mathrm{next}[l]\)。
也就是说从 \(l\) 一直往右开，最多只能开到 \(\mathrm{next}[l] - 1\) 的位置，而开不到 \(\mathrm{next}[l]\)。
则这个位置就必须满足 \(\mathrm{pre}[\mathrm{next}[l]] > \mathrm{pre}[l]\)，而且 \(\mathrm{next}[l]\) 必须是满足这个条件的第一个位置。
也就是说 \(\boldsymbol{\mathrm{next}[i]}\) 为满足 \(\boldsymbol{\mathrm{pre}[i] < \mathrm{pre}[k]}\) 且 \(\boldsymbol{i < k}\) 的第一个 \(\boldsymbol{k}\)，可以通过单调栈求出。
那么我们考虑令 \(\mathrm{val}[i] = \mathrm{pre}[\mathrm{next}[i]] - \mathrm{pre}[\mathrm{next}[i] - 1]\)，这也就是想要到达 \(\mathrm{next}[i]\) 需要给 \(g\) 增加的最小权值。
也就是说：想要到达 \(\mathrm{next}[i]\)，就必须在 \(g_l \sim g_{\mathrm{next}[i] - 1}\) 之间增加至少 \(\mathrm{val}[i]\)，具体加在哪里没有影响。
但是考虑到我们还要回来，就是说要从 \(r\) 向左回到 \(l\)，那么这个 \(\mathrm{val}[i]\) 还是加在尽量靠右的位置比较好。
也就是说 \(\mathrm{val}[i]\) 一定会全部加在 \(g_{\mathrm{next}[i] - 1}\) 上，也就是说 \(g_{\mathrm{next}[i] - 1} \gets g_{\mathrm{next}[i] - 1} + \mathrm{val}[i]\)。
这样就能在最优情况下成功到达 \(\mathrm{next}[i]\) 了，且此时油箱是空的，就可以继续处理 \(\mathrm{next}[i] \to r\) 的子问题了。
这样处理完之后，可以求出从 \(l\) 到 \(r\) 的最小代价，令它为 \(\boldsymbol{\mathrm{cost}(l, r)}\)。
但是此时不一定能成功从 \(\boldsymbol{r}\) 回到 \(\boldsymbol{l}\)。
因为只需要考虑从 \(r\) 回到 \(l\) 的情况，所以这时候要是回不来，直接把所有需要加的油都在 \(g_r\) 上加满就行了。
也就是说，刚刚从左到右的过程，会给 \(g_i\) 造成一些影响（\(g_{\mathrm{next}[i] - 1} \gets g_{\mathrm{next}[i] - 1} + \mathrm{val}[i]\)）。
进而会影响到 \(\mathrm{suf}[i]\) 的值，令被影响的新的 \(\mathrm{suf}\) 叫做 \(\mathrm{suf}'\)。
则从 \(r\) 无法回到 \(l\) 当且仅当存在一个位置 \(p\) 满足 \(l \le p \le r\) 且 \(\mathrm{suf}'[r] > \mathrm{suf}'[p]\)。
令 \(\mathrm{minsuf}'(l, r)\) 表示 \(\displaystyle \min_{l \le i < r} \{ \mathrm{suf}'[i] \}\)（注意 \(i\) 的范围是 \([l, r)\)，是左闭右开区间）。
则还需要在 \(g_r\) 上增加的代价就为 \(\max \{0, \mathrm{suf}'[r] - \mathrm{minsuf}'(l, r) \}\)。
综上所述，\(w(l, r)\) 应该等于 \(\mathrm{cost}(l, r) + \max \{0, \mathrm{suf}'[r] - \mathrm{minsuf}'(l, r) \}\)。
令 \(w'(l, r) = \mathrm{cost}(l, r) + \mathrm{suf}'[r] - \mathrm{minsuf}'(l, r)\)，也就是去掉了和 \(0\) 取 \(\mathrm{max}\) 的操作。
那么要求的就是满足 \(\mathrm{cost}(l, r) \le k\) 且 \(w'(l, r) \le k\) 的，最大的 \(r - l + 1\) 的值。
考虑计算某个左端点 \(l\) 的答案，可以记 \(S_l = \{\mathrm{next}[l], \mathrm{next}[\mathrm{next}[l]], \ldots \}\)。
可以发现这个是一个链状结构，把所有的 \(l \to \mathrm{next}[l]\) 的边画出来后，其实是一个树状结构（准确地说是森林）。
建立一个虚根 \(\mathrm{root}\)，所有的不存在 \(\mathrm{next}\) 的位置（也就是每个森林的根）连向 \(\mathrm{root}\)。
然后从 \(\mathrm{root}\) 开始 DFS，每次进入子树的时候考虑增加一个 \(\mathrm{next}\) 的贡献即可，也就是每次给 \(S_l\) 新添一个元素。
当左端点 \(l\) 固定时，需要找到的就是满足 \(\mathrm{cost}(l, r) \le k\) 且 \(w'(l, r) \le k\) 的最大的 \(r\)。
注意到 \(\mathrm{cost}(l, r)\) 关于 \(r\) 是个递增的函数，所以 \(\boldsymbol{r}\) 不能太大，先二分求出 \(\boldsymbol{r}\) 的上限。
而 \(w'(l, r)\) 有三部分，我们分别考虑：
对于 \(\mathrm{cost}(l, r)\)，每一个 \(S_l\) 的元素 \(x\) 会对 \(\mathrm{cost}(l, r)\) 产生一个后缀加的贡献（从 \(x\) 开始的后缀）。
对于 \(\mathrm{suf}'[r]\)，每一个 \(S_l\) 的元素 \(x\) 会对 \(\mathrm{suf}'[r]\) 产生一个后缀减的贡献（从 \(x\) 开始的后缀）。
很神奇的是：这两个贡献，作用的后缀完全相同，产生的贡献互为相反数，那么我们完全不管也是可以的。
也就是说： \(\mathrm{cost}(l, r) + \mathrm{suf}'[r]\)，这个值是固定不变的，它永远等于 \(\mathrm{suf}[r]\)。
最后，对于 \(\mathrm{minsuf}'(l, r)\)，每次对 \(\mathrm{suf}'\) 有一个后缀减的贡献（从 \(\boldsymbol{x - 1}\) 开始的后缀）。
之前定义为左闭右开区间的优势在这里显现出来了：
对于 \(r \ge x\) 的情况，会给 \(g_{x - 1}\) 加上 \(\mathrm{val}\)（注意是 \(x - 1\)），这是不好处理的（如果 \(r = x - 1\) 比较难办）。
但是定义为 \([l, r)\)，那么 \(g_{x - 1}\) 的修改就会在 \(\mathrm{minsuf}'(l, x)\) 上才显现出来，这就避免了 \(r = x - 1\) 时的问题。
那么也就是说，对于固定的 \(l\)，每个位置 \(r\) 的代价为 \(\mathrm{suf}[r] - \mathrm{minsuf}'(l, r)\)，考虑使用线段树维护这个代价。
而 \(r\) 的取值范围显然为 \(l \le r \le r_{\max}\)，其中 \(r_{\max}\) 为之前确定的上限。
注意到 \(\displaystyle \mathrm{minsuf}'(l, r) = \min_{l \le i < r} \{ \mathrm{suf}'[i] \}\)，其中这个 \(l \le i\) 不好处理，因为要计算很多个 \(l\) 的答案。
考虑在处理某个特定的 \(l\) 时，把 \(\mathrm{suf}'[1] \sim \mathrm{suf}'[l - 1]\) 加上 \(\infty\)，这样就取消了 \(i < l\) 的影响。
这之后 \(\mathrm{minsuf}'(l, r)\) 就可以看作是 \(\displaystyle \min_{1 \le i < r} \{ \mathrm{suf}'[i] \}\) 了。
对于 \(r \le r_{\max}\) 的限制我们也如法炮制，把 \(\mathrm{suf}'[r_{\max}] \sim \mathrm{suf}'[n]\) 减去 \(\infty\)，即可消除 \(r > r_{\max}\) 的影响。
（注意是包括 \(\mathrm{suf}'[r_{\max}]\)，这样才能把 \(\mathrm{minsuf}'(l, r_{\max} + 1)\) 给变成 \(-\infty\)）
当然，对于 \(\boldsymbol{l \le r \le r_{\max}}\) 的处理，可以直接在线段树上提取区间，但复杂度可能会退化为 \(\boldsymbol{\mathcal O (n \log^3 n)}\)。
（存在一种精细实现的方法使得复杂度不退化，但是需要先把所有区间提取出来，再从左到右扫一遍，从右到左查询，最后可以得到时间复杂度为 \(\mathcal O (n \log^2 n)\)，实现起来有点复杂）
所以最终就变成了一个线段树维护 \(\displaystyle a_i - \min_{1 \le j < i} \{ b_j \}\) 的最小值的问题，然后对于修改需要支持 \(b_i\) 的区间加减法。
这个东西怎么维护呢？
考虑一个类似楼房重建的线段树算法：
线段树中的每个节点维护区间 \(\mathrm{suf}[i], \mathrm{suf}'[i]\) 的最小值，
再特别维护一个：仅考虑本区间的 \(\mathrm{suf}'[i]\) 时，\(r\) 的取值仅在右子树的答案的最小值。
在 Pushup 的时候使用一个类似楼房重建的每次只递归到一个子树内的函数维护当前节点信息。
在查询答案时，使用一个类似线段树上二分的结构求得最靠右的满足 \(w'(l, r) \le k\) 的下标 \(r_{\mathrm{ans}}\)。
这部分与楼房重建相比，还是有很多新的东西，需要再详细说一下：
当区间左侧传来的最小值 \(pre\) 比左子树的 \(\mathrm{suf}'[i]\) 的最小值小时，也就是左子树完全被 \(pre\) 控制，
也就是，左子树中的条件变为 \(\mathrm{suf}[i] - pre \le k\)，就是 \(\mathrm{suf}[i] \le k + pre\)，这部分是正常的线段树上二分。
但是不要忘记了还要递归进右子树查询，虽然两边子树都递归了，但是时间复杂度没有退化到 \(\mathcal O (n)\)。
因为每次递归到左子树时，都是 \(\mathcal O (\log n)\) 的，而可能有 \(\mathcal O (\log n)\) 次向左子树的递归，所以是 \(\mathcal O (\log^2 n)\) 的。
具体细节请见从《楼房重建》出发浅谈一类使用线段树维护前缀最大值的算法。
时间复杂度为 \(\mathcal O (n \log^2 n)\)，评测链接。
cf578F
令矩阵中为 * 的格子的个数为 \(k\)。
\(n \times m\) 的网格，就有 \((n + 1) \times (m + 1)\) 个格点，我们把格点交错黑白染色。
则可以发现，每个镜子都是连接两个同色格点。如果我们把每面镜子看作一条边，则合法的图有什么性质呢？
可以发现，要么所有的黑点连成一棵树，要么所有的白点连成一棵树，分别对应同一条光线在射入的格子的顺时针一格或者逆时针一格射出的情况。
而如果其中一种颜色连成了一棵树，那么另一种颜色的连边方案就被唯一确定了。
因为保证了 \(k \le 200\)，所以使用并查集合并一些点后，剩余点数为 \(\mathcal O (n + m + k)\) 个。
再使用矩阵树定理即可得到答案。
时间复杂度为 \(\mathcal O (n m \alpha(n m) + {(n + m + k)}^3)\)，评测链接。
2020-03-09
cf708D
这是一个有源汇带上下界最小费用可行流的问题，然而这个“带上下界”其实是假的。
注意到，只要 \(f\) 在 \(0 \sim c\) 内，就可以用 \(1\) 的代价更改，但是一旦要超过 \(c\)，就需要同时更改 \(c\)，相当于代价为 \(2\)。
对 \(f \le c\) 的边和 \(f > c\) 的边分开考虑：
- 如果 \(f \le c\)，则最终的 \(f'\) 可以减小或增大，故连如下三条边：
- 减小 \(f\)：也就是从 \(v\) 到 \(u\) 退流，连 \(v \to u\)，容量为 \(f\)，费用为 \(1\)。
- 增大 \(f\)（\(f \le c\) 的部分）：连 \(u \to v\)，容量为 \((c - f)\)，费用为 \(1\)。
- 增大 \(f\)（\(f > c\) 的部分）：连 \(u \to v\)，容量为 \(\infty\)，费用为 \(2\)。
- 如果 \(f > c\)，则至少要花费 \((f - c)\) 的代价，且在 \(c \le f' \le f\) 时取到，故先贡献 \((f - c)\)，连如下三条边：
- 减小 \(f\)，最终的 \(f'\) 在 \(c \sim f\) 之间：连 \(v \to u\)，容量为 \((f - c)\)，费用为 \(0\)。
- 减小 \(f\)，最终的 \(f' \le c\)：连 \(v \to u\)，容量为 \(c\)，费用为 \(1\)。
- 增大 \(f\)：连 \(u \to v\)，容量为 \(\infty\)，费用为 \(2\)。
然后对于初始的每条边，连 \(u \to v\)，容量下界和上界均为 \(f\)，费用为 \(0\)。
实际上，因为本题中的上下界把“有源汇带上下界可行流”转化成普通最大流，就是：
新建超级源和超级汇 \(S, T\)。
如果 \(u\) 点流入比流出多，就连 \(S \to u\)，容量为流入流出的差值，费用为 \(0\)。
如果 \(u\) 点流出比流入多，就连 \(u \to T\)，容量为流出流入的差值，费用为 \(0\)。
最后，为了取消原来的源汇，新建一条 \(n \to 1\)，容量为 \(\infty\)，费用为 \(0\)。
然后跑一次超级源到超级汇的最小费用最大流，一定是满流的，转化回原图就是一个最小费用可行流了。
如果使用 SPFA 辅助实现的类 Dinic 算法求最小费用最大流，时间复杂度为 \(\mathrm{MCMF}( \!\left< |V|, |E|, F \right>\! = \!\left< \mathcal O(n), \mathcal O(n + m), \mathcal O (mv) \right>) = \mathcal O (n (n + m) m v)\)，其中 \(v\) 为值域，本题中为 \({10}^6\)。
时间复杂度为 \(\mathcal O (n (n + m) m v)\)，评测链接。
cf538H
也就是要把老师分成两组，满足每组的 \([l_i, r_i]\) 的交集，“相加”后与 \([t, T]\) 有交。
如果有三个老师的 \([l_i, r_i]\) 两两无交集，那么就完蛋了，根本没法分组。
否则，如果我们考虑其中一组的人数为 \(n_1 = \min \{ r_i \}\)，另一组的人数为 \(n_2 = \max \{ l_i \}\)。
如果 \(n_1 \ge n_2\)，也就是所有老师的 \([l_i, r_i]\) 两两有交的情况，那么这种情况下每个老师都可以任意选组。
如果 \(n_1 < n_2\)，那么这也是最“松”的一种方案了，如果 \(n_1\) 增大或 \(n_2\) 减小都会导致某个老师无法选组的情况。
那么，也就是说 \(n_1\) 只能减小，\(n_2\) 只能增大。
然而，现在 \(n_1 + n_2\) 还不一定满足在 \([t, T]\) 内的情况。
所以如果 \(n_1 + n_2 < t\)，就只能增大 \(n_2\)；如果 \(n_1 + n_2 > T\)，就只能减小 \(n_1\)。
那么就可以算出最优的一个 \(n_1\) 和 \(n_2\) 的选取方案，再根据这个方案对老师进行一次二分图染色判定即可。
时间复杂度为 \(\mathcal O (n + m)\)，评测链接。
2020-03-10
cf704E
套路树链剖分，然后观察一条链的情况：
有一个数轴，上面会有点突然出现，然后移动，最后消失，问最早的两点重合的时间。
把所有链的时间取 \(\min\) 即可得到答案。
对于一个数轴，我们把时间维也显示出来，然后画出每个点的“世界线”（物体在时空中的轨迹）。
可以发现，每个点的轨迹都是一条线段，只要算出在时间维度上的最早的交点即可。
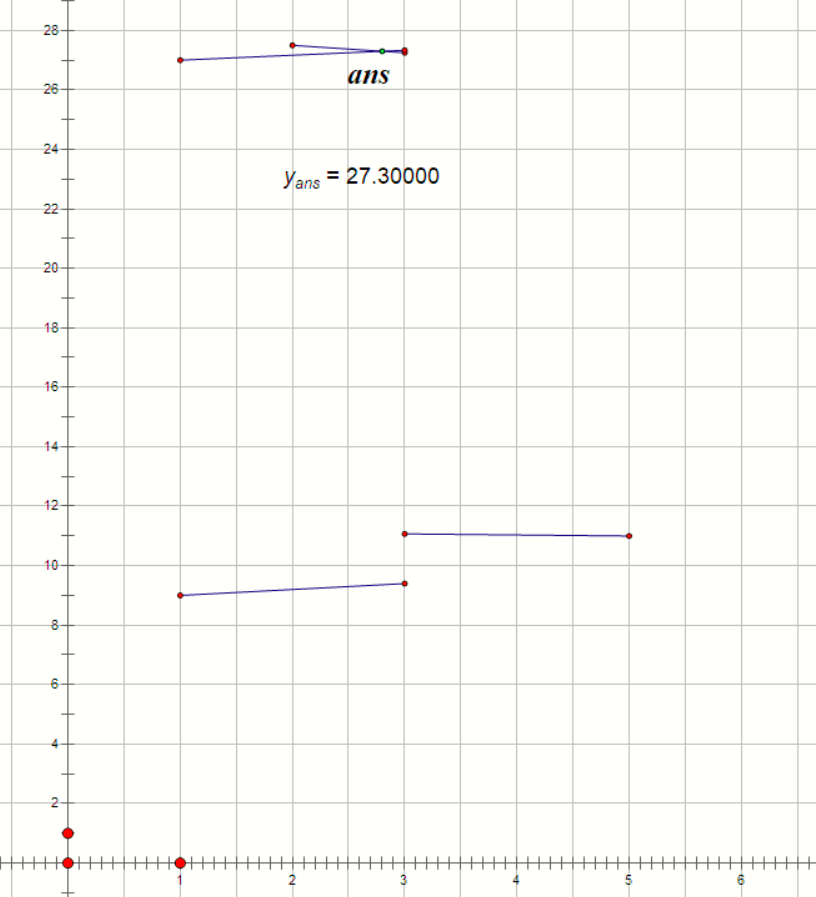
如图，这是样例 #1 的情况，考虑的重链为 \(1 - 4 - 6 - 5 - 2\) 这条，答案为 \(27.3\)。
我们看一下交点附近的细节：
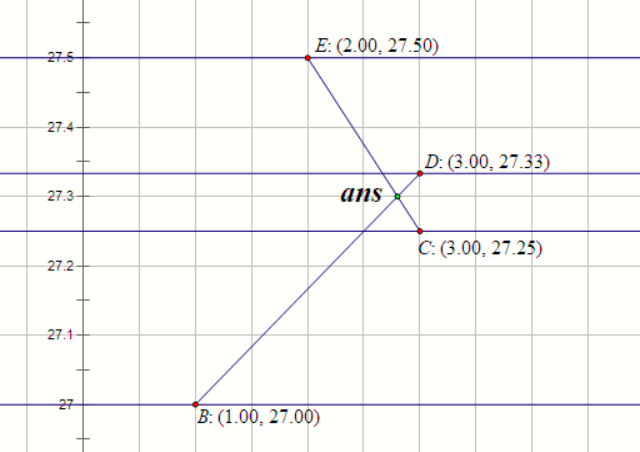
到底要怎么找到并确定这个交点的坐标呢？如果两两判断那必然是不行的，而且交点确实也可能有 \(\mathcal O (m^2)\) 个。
从“找到最早的交点”出发，我们考虑按照时间从小到大做扫描线。
考虑这样的一个“第一个交点”，我们可以发现，交出它的两条线段，一定在之前的某一个时刻，是相邻的。
也就是说，不可能之前的每个时刻都有至少一条线段挡在它们之间，考虑反证法显然。
那么我们只需要动态维护在扫描线过程中的，相邻线段的交就行了。
扫描线无非就是加入一条线段，删除一条线段，也就是说只要维护加入和删除的时候的旁边两条线段就行。
那么最终只有 \(\mathcal O (m)\) 对相邻线段，这是很重要的一步转化。
那么我们需要一个合适的数据结构来寻找相邻线段并能够维护加入删除线段。
令人意想不到的是，我们的 set 居然就满足条件。set 中存当前的线段，但是排序方式怎么办呢？
我们使用一个全局变量 \(T\) 来控制线段在 \(t\) 时刻下的横坐标位置，然后使用横坐标位置排序即可。
因为只要没有交点，线段之间的相对位置就不会改变，这是不会触发 set 的未定义行为的。
当然，如果 \(T\) 已经大于等于当前求出的交点时刻，就要及时退出，不要调用 set，以免触发 UB 导致不好的结果。
要注意的是，也不要一求出交点就退出，第一个求出的交点不一定是最早的交点。
时间复杂度为 \(\mathcal O (m \log m \log n)\)，评测链接。
cf696F
最优情况下，一定是一个点控制凸多边形的连续若干条边，另一个点也是连续若干条边。
那么我们考虑先二分答案，然后尺取法确定以每条边为左端点时，右端点最多到哪里。
具体实现时用半平面交即可。
时间复杂度为 \(\mathcal O (n^2 (\log v - \log \varepsilon))\)，其中 \(v\) 为值域，评测链接。
2020-03-11
cf666D
实际上是一个暴力憨批题，从它只有 \(50\) 组数据也看得出来。
每个点要么横着动要么竖着动，枚举一下。
然后画出每个点可以到达的位置的轨迹，也就是四条线，但是可能重合。
有很多情况，可以发现只有这三种情况可能有解：
- 横线竖线都 \(2\) 条，当且仅当它们的 \(4\) 个交点组成正方形时有解，然后再枚举点对配对情况。
- 横线 \(2\) 条竖线 \(1\) 条（或反过来），那么正方形的顶点一定是那两个交点，然后再枚举是往哪一边。
- 横线 \(2\) 条没有竖线（或反过来），徒手解一下整数规划（大雾）就行。
然后就没了。
时间复杂度为 \(\mathcal O (t)\)，评测链接。
2020-03-12
cf516E
令 \(d = \gcd(m, n)\)，则可以发现，每一天，只有编号对 \(d\) 取余相同的一对男女生会一起玩。
也就是说，编号模 \(d\) 不同余的两人永远不会产生直接或间接关系，可以分开考虑。
那么就分成了 \(d\) 个子问题，第 \(i\)（\(0 \le i < d\)）个子问题包含所有 \((x \bmod d) =i\) 的编号为 \(x\) 的人。
算出第 \(i\) 个子问题的答案之后，乘以 \(d\) 再加上 \(i\) 就能得到原问题的这个部分的答案，所有答案取 \(\max\) 即可。
由裴蜀定理，只要子问题中有一个人是快乐的，那么最终这个子问题中的所有人都会变得快乐。
特别地，如果 \(d > g + b\)，则因为至少存在一个子问题没有快乐的人，所以原问题无解。
这样就帮我们排除掉了 \(d\) 太大的情况，现在 \(1 \le d \le 2 \times {10}^5\)。
那么我们让 \(m, n\) 都除掉 \(d\)，只需要考虑这个子问题，注意此时 \(m, n\) 互质。
需要注意的是，如果所有人一开始就是快乐的（子问题可能存在此情况），请返回 \(-1\) 而不是 \(0\)，要不然会出错。
而如果所有人都不是快乐的，请返回无解。否则就考虑一般情况：
我们考虑单独计算最后一个女生变快乐的天数和最后一个男生变快乐的天数，取 \(\max\) 得到答案。
假设最后一个变快乐的女生是 \(i\) 号，那么她一定是在第 \(x\) 天变快乐的，满足 \((x \bmod m) = i\)。
假设是因为 \(j\) 号男生变快乐的，这里 \(j = (x \bmod n)\)，那么就需要考虑 \(j\) 号男生是什么时候变快乐的。
如果 \(j\) 号男生一开始就是快乐的，那么显然他会在第 \(j\) 天让 \((j \bmod m)\) 号女生变快乐。
令 \(c = (x - j) / n\)，也就是从他让 \((j \bmod m)\) 号女生变快乐，直到他让 \(i\) 号女生变快乐之间经过的轮数。
则我们考虑在第 \((j + n)\) 天，这个男生会让 \(((j + n) \bmod m)\) 号女生变快乐。
一直到第 \((j + c n)\) 天，也就是第 \(x\) 天，他会让 \(((j + c n) \bmod m)\) 号女生，也就是 \(i\) 号女生变快乐。
那么我们是不是可以说，是 \(\boldsymbol{(j \bmod m)}\) 号女生，在经过 \(\boldsymbol{c}\) 轮（\(\boldsymbol{c n}\) 天）之后，让 \(\boldsymbol{((j + cn) \bmod m)}\) 号女生，也就是 \(\boldsymbol{i}\) 号女生变快乐的。
或者简化地说，如果 \(\boldsymbol{k}\) 号女生变快乐了，那么在 \(\boldsymbol{n}\) 天之后，\(\boldsymbol{((k + n) \bmod m)}\) 号女生一定会变快乐。
反复利用这个简化的结论 \(c\) 次，就可以推出 \(c n\) 天之后让 \(((k + cn) \bmod m)\) 号女生变快乐的结论。
也就是说，对于每个女生 \(k\)，连一条从 \(k\) 出发，到达 \(((k + n) \bmod m)\) 的边，边权为 \(n\)。
- 这表示 \(k\) 号女生在某一天变快乐了，那么 \(n\) 天后，\(((k + n) \bmod m)\) 号女生会变快乐。
然后，对于每个一开始就是快乐的男生 \(j\)，从源点 \(S\) 连一条到达 \((j \bmod m)\) 的边，边权为 \(j\)。
- 这表示 \(j\) 号男生会在第 \(j\) 天，第一次让 \((j \bmod m)\) 号女生变快乐，之后就是女生之间自己连边的事情了。
最后，对于每个一开始就是快乐的女生 \(i\)，从源点 \(S\) 连一条到达 \(i\) 的边，边权为 \(i\)。
- 这表示从第 \(i\) 天开始，这个女生就可以每 \(n\) 天让另一个女生变快乐。
求出 \(S\) 到每个点的最短路，对于一个一开始不是快乐的女生，\(S\) 到她的最短距离就会对答案产生贡献。
注意，对于一个一开始就是快乐的女生，不产生贡献，因为她并不是在第 \(i\) 轮才变快乐的，而是从一而终都快乐。
但是总点数是 \({10}^9\) 级别的，没法做。
注意到第一类边很有特点，把所有女生连成了一个大环。
但是环上的点是每次 \(x \to ((x + n) \bmod m)\) 的，不按顺序。
我们用某种方式把这些点重标号，然后注意到只需要考虑二三类边中，与 \(S\) 相连的关键点即可。
把这些关键点按照在环上的顺序排序，就可以快速处理最短路了。
以上是对女生的考虑，如果是男生同理，只要转换一下就行。
时间复杂度为 \(\mathcal O ((b + g) \log (b + g))\)，评测链接。
agc027_f
首先我们看看这两棵树是否完全一样，是的话输出 \(0\) 然后走人。
否则我们枚举第一次操作：选了某个叶子 \(u\)，然后把它接到 \(v\) 上（\(v\) 不一定是 \(u\) 原来连接的点）。
那么我们发现，\(u\) 不能再被选择了，那么考虑在两棵树（注意这里是新的 \(A\)）中都把 \(u\) 当作根。
把“新的 \(A\)”和 \(B\) 以 \(u\) 为根拎起来后，就很容易看出，因为树根不能动，所以操作都是从叶子开始。
也就是说：如果不去操作一个点 \(x\) 的话，那么 \(x\) 的双亲节点将永远不会改变。
但是如果操作了一个点的话，又把它接回原来的位置显然不优，所以可以得出结论：
- 一个点被操作，当且仅当它在两棵树中的双亲节点不同。
如果一个点不被操作，但是它的双亲节点要被操作，这是不可能的，因为它的双亲节点没有成为叶子的机会。
这是一个判无解的依据。
其次我们可以发现，在“新的 \(A\)”中，一个点一定比它的双亲节点更早被操作（假设它们都需要被操作）。
类似地，在 \(B\) 中，一个点一定比它的双亲节点更晚被操作。
那么我们把这个关系连边，如果可以成功拓扑排序，则自然有解，且拓扑排序的过程就构造了一个合法方案。
那么每次建图并跑拓扑排序的时间复杂度为 \(\mathcal O (N)\)。
时间复杂度为 \(\mathcal O (T N^3)\)，评测链接。
2020-03-13
agc024_f
我们直接考虑所有 \((2^{N + 1} - 1)\) 个长度在 \(0 \sim N\) 之间的 \(01\) 串，计算它们到底是多少个 \(S\) 中的串的子序列。
当枚举的串为 \(A\) 时，令这个值为 \(\mathrm{val}(A)\)，这样直接枚举所有 \(01\) 串就能得到答案了。
我们考虑子序列自动机，也就是在判定一个串 \(A\) 是不是另一个串 \(B\) 的子序列时：
比如 \(A = \mathtt{011001}\)，\(B = \mathtt{110110101}\)，因为 \(A\) 中的第一个字符是 \(\texttt{0}\)，考虑 \(B\) 中第一个 \(\texttt{0}\) 的位置。
用 \(A\) 的第一个字符 \(\texttt{0}\) 去匹配 \(B\) 中的第一个 \(\texttt{0}\)，则转化为 \(A = \mathtt{11001}\)，\(B = \mathtt{110101}\)。
所谓“子序列自动机”的好处在于它的匹配过程是唯一的。
那么，我们这样考虑：对于一个 \(01\) 串 \(C \in S\)，我们希望 \(C\) 的所有子序列 \(A\) 的 \(\mathrm{val}\) 值都加上 \(1\)。
那么考虑 DP：令 \(\mathrm{dp}(A | B)\) 表示使用 \(A\) 去匹配某个原串 \(C \in S\)，匹配剩下的串是 \(B\)，原串 \(C\) 的方案数。
比如 \(\mathrm{dp}(\mathtt{00} | \mathtt{110110101})\) 可以转移到：
- 匹配了第一个 \(\mathtt{0}\)：\(\mathrm{dp}(\mathtt{000} | \mathtt{110101})\)。
- 匹配了第一个 \(\mathtt{1}\)：\(\mathrm{dp}(\mathtt{001} | \mathtt{10110101})\)。
- 停止匹配：\(\mathrm{dp}(\mathtt{00} | \varepsilon)\)。
则可以发现，\(\mathrm{val}(A) = \mathrm{dp}(A | \varepsilon)\)。关于边界条件，令 \(\mathrm{dp}(\varepsilon | C) = 1\) 即可（\(C \in S\)）。
这样 DP 的话，因为过程中 \(|A| + |B| \le N\)，所以状态总数是 \(\mathcal O (N 2^N)\) 的。
使用合适的方法存储状态，就可以做到 \(\mathcal O (N 2^N)\) 的复杂度。
时间复杂度为 \(\mathcal O (N 2^N)\)，评测链接。
2020-03-14
agc027_e
我们考虑判断一个字符串 \(t\) 能否通过 \(s\) 变换得到。
假设可以，则对于 \(t\) 的每一个字符，都对应了 \(s\) 中的一段连续区间。
也就是，\(s\) 的一个子串，经过若干次操作后，变成了单一的一个字符 \(\mathtt{a}\) 或 \(\mathtt{b}\)。
这里有个很有趣的结论：如果我们把 \(\mathtt{a}, \mathtt{b}\) 分别看作 \(1, 2\)，则执行操作是不会改变所有字符之和模 \(3\) 的结果的。
也就是说，定义 \(p(s)\) 为字符串 \(s\) 中所有字符之和模 \(3\)，则 \(s\) 经过若干次操作变成 \(t\)，\(p(s)\) 与 \(p(t)\) 是相等的。
那么回到变成字符的问题上来，如何判断 \(s\) 能不能变成单一的字符 \(\mathtt{a}\) 或 \(\mathtt{b}\) 呢？
显然 \(p(s)\) 应该等于 \(1\) 或者 \(2\)，这对应了最终变成的是 \(\mathtt{a}\) 或者是 \(\mathtt{b}\)，显然这是必要条件。
但是这并不是充分条件，考虑 \(s = \mathtt{ababa}\)，虽然 \(p(s) = p(\mathtt{a})\)，但是根本没法对 \(s\) 进行操作，所以不可行。
如果 \(s\) 中存在两个相邻的相同字符呢？事实证明，再加上这个条件就是充分的了。
考虑归纳：当 \(|s| \le 2\) 时成立；否则只要对一个和异种字符相邻的位置进行操作，就能使长度变小 \(1\) 且还满足条件。
也就是说，字符串 \(\boldsymbol{s}\) 能变成单个字符 \(\boldsymbol{c}\) 当且仅当 \(\boldsymbol{p(s) = p(c)}\) 且「\(\boldsymbol{|s| = 1}\) 或 \(\boldsymbol{s}\) 中存在相邻的相同字符」。
那么再回到一开始的问题：字符串 \(t\) 能否通过 \(s\) 变换得到？
很自然地，有一个贪心匹配的算法：
依次考虑 \(t\) 中的每一个字符，选择一个 \(s\) 的最短前缀变换成这个字符，然后删掉这个前缀继续匹配。
举个例子，当 \(t = \mathtt{abba}\) 且 \(s = \mathtt{aabbabaabaaabab}\) 时：
- \(t_1 = \mathtt{{\color{red}{a}}}\)，选取 \(s\) 的满足条件的最短前缀：\(s = \mathtt{{\color{red}{a}}abbabaabaaabab}\)。
- \(t_2 = \mathtt{{\color{blue}{b}}}\)，选取 \(s\) 的满足条件的最短前缀：\(s = \mathtt{{\color{red}{a}}{\color{blue}{abb}}abaabaaabab}\)。
- \(t_3 = \mathtt{{\color{purple}{b}}}\)，选取 \(s\) 的满足条件的最短前缀：\(s = \mathtt{{\color{red}{a}}{\color{blue}{abb}}{\color{purple}{abaa}}baaabab}\)。
- \(t_4 = \mathtt{{\color{green}{a}}}\)，选取 \(s\) 的满足条件的最短前缀：\(s = \mathtt{{\color{red}{a}}{\color{blue}{abb}}{\color{purple}{abaa}}{\color{green}{baa}}abab}\)。
最后 \(s = \mathtt{{\color{red}{a}}|{\color{blue}{abb}}|{\color{purple}{abaa}}|{\color{green}{baa}}|abab}\)，被分成了五段（前 \(|t|\) 段加上一个未匹配的后缀）。
特别地，这个最后一段需要满足 \(\boldsymbol{p}\) 值为 \(\boldsymbol{0}\)，例如这里 \(p(\mathtt{abab}) = 0\)（因为需要满足 \(p(s) = p(t)\)）。
我们可以证明：\(s\) 能变成 \(t\) 当且仅当能够成功分段，且 \(s\) 存在两个相邻的相同字符（或 \(t = s\)）。
注意：证明部分可以酌情跳过！
注意：证明部分可以酌情跳过！
注意这里包含了两个条件，第一个是成功分段，第二个是 \(s\) 存在相邻的相同字符。
我们先考虑 \(s\) 不存在相邻的相同字符的情况，显然输出 \(1\) 即可（当 \(t = s\) 时）。
那么在后续证明中假定 \(s\) 存在相邻的相同字符，条件变为：能够成功分段。
我们首先证明它的必要性，即任意一个合法的 \(t\) 都能够成功分段：
- 对于某个 \(t\)，我们考虑它在 \(s\) 中对应的每个段。
- 即 \(s = s_1 \, s_2 \, \cdots \, s_{|t|}\)，这里每个 \(s_i\) 都是一个字符串，且 \(s_i\) 变成了 \(t\) 的第 \(i\) 个字符。
- 假设 \(t_i\) 对应的 \(s_i\) 是第一个非最短前缀（也就是说之前的字符对应的前缀都是最短的）。
- 令此时的最短前缀为 \(x\)，则 \(s_i = x \, y\)，其中 \(p(y) = 0\)。
- 因为 \(p(y) = 0\)，考虑把 \(y\) 并入后一个 \(s_{i + 1}\)，以保证 \(s_i\) 的最短性。
- 如果 \(s_{i + 1}\) 不存在，也就是 \(i = |t|\)，则结论自然成立（\(y\) 成为最后一段未匹配后缀）。
- 否则当前的 \(s_{i + 1} \gets y \, s_{i + 1}\)，此时至少需要保证 \(s_{i + 1}\) 是合法的，如果合法就可以继续递归。
- 但是问题在于可能不合法，可以发现此时 \(|s_{i + 1}| \ge 2\)，那么就是 \(s_{i + 1}\) 中不存在相邻的相同字符。
- 也就是形如 \(y = \mathtt{baba}\)，而原先的 \(s_{i + 1} = \mathtt{b}\) 的这种形式，新的 \(s_{i + 1} = \mathtt{babab}\)。
- 那么我们注意到，如果把 \(s_{i + 1}\) 拆分为 \(\mathtt{b|abab}\) 两段，然后把 \(\mathtt{abab}\) 继续并入后面进行讨论。
- 这样就可以保证此时的 \(s_{i + 1} = \mathtt{b}\)，显然是最短的，然后把问题转移到后面了，递归即可。
- 所以我们证明了：任意一个合法的 \(t\) 都能够成功分段。
还需要证明它的充分性，即只要能够成功分段，那就一定是合法的：
- 考虑最终分段的情况，假如不存在最后一段未匹配后缀，则自然成立，否则：
- 假设 \(s = s_1 \, s_2 \, \cdots \, s_{|t|} \, s_{|t| + 1}\)，其中 \(s_{|t| + 1}\) 是未匹配后缀，我们要想办法把这个后缀塞到前面去。
- 首先直接把 \(s_{|t|}\) 与 \(s_{|t| + 1}\) 合并，如果可行就合法，不过如果不可行呢？
- 类似地，自然有形如 \(s_{|t|} = \mathtt{a}\) 和 \(s_{|t| + 1} = \mathtt{baba}\) 这种形式。
- 那么我们令 \(s_{|t|} = \mathtt{a}\)，然后把 \(\mathtt{abab}\) 往前转移。
- 因为有「\(s\) 中存在相邻的相同字符」这个条件，这个过程一定会因为合并出了相邻的相同字符而停止。
- 所以我们证明了：任意一个能够成功分段的 \(t\) 都是合法的。
证明部分结束。
证明部分结束。
那么我们先特判 \(s\) 是 \(\mathtt{ababababa}\) 这种形式，直接输出 \(1\)，否则考虑做一个这样的 DP：
令 \(dp(i)\) 表示考虑了 \(s\) 从 \(\boldsymbol{i}\) 开始的后缀，能够成功分段的 \(t\) 的数量（注意最后未匹配的后缀的 \(p = 0\) 的限制）。
则答案就是 \(dp(1)\)，转移是比较显然的。
我代码中实现的时候，为了方便，把 \(t\) 是空串的情况也计入答案，输出的时候要扣除。
时间复杂度为 \(\mathcal O (|s|)\)，评测链接。
2020-03-16
cf526G
可以证明：使用 \(k\) 条路径就可以覆盖一棵有 \(2 k\) 的叶子的树。
先以任意方式匹配叶子。如果有两条路径不相交，可以调整成相交的情况。
不断调整就可以让任意两条路径都相交，于是显然覆盖了整棵树。
（证明不严谨，因为没有说明调整能在有限步内结束，不过这不重要）
所以当询问 \(y\) 的时候，就是要在原树中选取不超过 \(2 y\) 个叶子，让这些叶子组成的极小连通块的边权和尽量大。
再考虑：每次询问中，一定存在一种方案使得直径的两端中至少有一端被选取。
那么我们以两个直径端点为根，每次询问在两棵树中分别查询即可。
那么，现在根是一个叶子（直径端点必然是叶子），且根必选。
也就是说，需要选其它至多 \(2 y - 1\) 个叶子，打通他们到根的链，并且最大化边权和。
考虑带边权的长链剖分，发现这和选取过程是等价的，也就是贪心地选取前 \(2 y - 1\) 个最长链即可。
但是选完之后不一定经过 \(x\)，所以需要做一下调整。
首先打通 \(x\) 子树中最深的点到根的路径，然后需要去掉另一个叶子，使得减小量尽量小。
可以发现，要不然是删掉第 \(2 y - 1\) 个最长链，也就是仅选取前 \(2 y - 2\) 个最长链，然后把 \(x\) 接上。
要不然就是在选取前 \(2 y - 1\) 个最长链的基础上，先把 \(x\) 接上，然后删去第一个碰到的点的其它子树。
最优解，一定符合这两种情况之一，且不会统计到错误的情况（叶子数都不超过 \(2 y - 1\)），所以是正确的。
时间复杂度为 \(\mathcal O ((n + q) \log n)\)，评测链接。
2020-03-17
cf700E
后缀数组再次证明了：SAM 能做的题，SA 也能做。
我们尝试改变一下定义，强制让 \(t_{i + 1}\) 是 \(t_i\) 的 border，如果不是的话可以减小 \(t_i\) 的长度，显然不更劣。
在这样的调整下，我们发现可以这样定义：
令 \(\mathrm{cool}(s)\) 表示强制要求 \(t_1 = s\) 以及 \(t_{i + 1}\) 是 \(t_i\) 的 border 的，最大的 \(k\) 值。
那么要求的即是 \(s\) 的所有子串中的最大的 \(\mathrm{cool}\) 值。
因为我们考虑使用 SA，所以令 \(\mathrm{f}[i]\) 表示 \(s\) 以 \(i\) 开始的后缀的所有前缀中的最大的 \(\mathrm{cool}\) 值。
然后我们考虑转移，显然从后往前转移（后缀的长度递增）是比较合理的。
假设我们要利用后面的信息求出 \(\mathrm{f}[i] = k\)，根据定义，要么 \(\mathrm{f}[i] = 1\)，要么有 \(t_2\) 是 \(t_1\) 的 border。
而如果 \(t_2\) 是 \(t_1\) 的 border，显然 \(t_2\) 不仅是 \(s[i : n]\) 的一个前缀，而且还必须在 \(s[i + 1 : n]\) 中出现过至少 \(1\) 次。
而且我们还有 \(\mathrm{cool}(t_2) = k - 1\)。
那么我们考虑后面的所有 \(\mathrm{f}[j] = k - 1\) 的位置，它们就有可能转移给 \(\mathrm{f}[i]\)，然而实际上我们并不知道 \(k\) 的值。
也就是说，与其考虑一个位置从后转移而来，不如换个角度，考虑让一个位置向前转移。
但是转移的过程却和后缀的 LCP 以及 \(\mathrm{f}[i]\) 对应的前缀长度息息相关：
一个 \(i\) 能转移到更前面的 \(j\) 当且仅当 \(\mathrm{LCP}(j, i) \ge |s_i|\)，其中 \(s_i\) 即为 \(\mathrm{cool}(s_i) = \mathrm{f}[i]\) 的一个 \(s[i : n]\) 的前缀。
可以发现，当有多个满足条件的 \(\boldsymbol{s_i}\) 时，取最短的 \(\boldsymbol{s_i}\) 才是正确的。
这提示我们可能需要再维护一个对应的 \(s_i\) 长度的信息，记作 \(\mathrm{len}\)。如果 \(\mathrm{f}[i] = 1\)，显然 \(\mathrm{len}[i] = 1\)。
这时你可能会想出这样的转移过程：
如果 \(\mathrm{LCP}(j, i) \ge \mathrm{len}[i]\)，那么 \(\mathrm{f}[j] = \mathrm{f[i]}\)，\(\mathrm{len}[j] = \mathrm{len[i]} + i - j\)。
（当然要在以 \(\mathrm{f}\) 尽量大的前提下，让 \(\mathrm{len}\) 尽量小）
但是很可惜这样是错误的，考虑 \(s = \mathtt{acacaba}\)。
对于位置 \(7\) 有 \(\langle \mathrm{f}, \mathrm{len} \rangle = \langle 1, 1 \rangle\)，转移给位置 \(1, 3, 5\)。
对于位置 \(5\) 有 \(\langle \mathrm{f}, \mathrm{len} \rangle = \langle 2, 3 \rangle\)，注意它无法转移给 \(1\) 和 \(3\)。
但是，对于位置 \(3\)，真实的 \(\langle \mathrm{f}, \mathrm{len} \rangle\) 应该为 \(\langle 2, 3 \rangle\)，然而在这里变成了 \(\langle 2, 5 \rangle\)，是被位置 \(7\) 而非位置 \(5\) 转移的。
进而影响到位置 \(1\) 的值，最终影响答案，正确答案为 \(3\) 但是这样求出来的答案为 \(2\)。
如果位置 \(5\) 当 \(\mathrm{f} = 1\) 时的 \(\mathrm{len}\) 也能转移给位置 \(3\) 就好了，但是这是不现实的，因为 \(\mathrm{f}\) 可能太大无法一一转移。
其实正确方法是，不用同时维护 \(\mathrm{len}\) 了，直接在使用时计算 \(\mathrm{len}\) 即可。
因为实际上，如果 \(\mathrm{len}\) 的计算正确，是不会影响 \(\mathrm{f}\) 值的转移的，但是问题出在 \(\mathrm{len}\) 的计算上。
如果我们已知 \(\mathrm{f}[i] = k\)，能否同时确定 \(\mathrm{len}\) 的值呢？
- 如果 \(k = 1\)，则 \(\mathrm{len}[i] = 1\)。
- 否则我们还需要知道 \(\mathrm{f}[i]\) 是从哪个 \(\mathrm{f}[j] = k - 1\) 处转移而来的。
- 如果有多处，应该选择 \(\mathrm{len}[j]\) 最小的那一处。
- 获得了 \(\mathrm{len}[j]\) 之后，我们在 SA 中定位 \(\mathrm{LCP}(i, x) \ge \mathrm{len}[j]\) 的可行的 \(x\) 的区间。
- 在线段树中查询这个区间内，在 \(i\) 之后的，且离 \(i\) 尽量近的位置 \(y\)。
- 则 \(\mathrm{len}[i] = \mathrm{len}[j] + y - i\)。
确定了 \(\mathrm{len}[i]\) 之后，就可以往前转移了。在 SA 中定位 \(\mathrm{LCP}(x, i) \ge \mathrm{len}[i]\) 的可行的 \(x\) 的区间。
然后用线段树，转移给区间内的所有在 \(i\) 之前的位置，线段树要维护在 \(k\) 尽量大的前提下让 \(\mathrm{len}\) 尽量小。
时间复杂度为 \(\mathcal O (n \log n)\)，评测链接。
2020-03-18
agc030_c
注意到 \(N\) 的上界是 \(K / 2\)，那么我们考虑在大小约为 \(K / 2\) 的矩阵中构造方案。
先不考虑限制，注意到这样的矩阵满足条件：\(\begin{bmatrix} 1 & 1 & \cdots & 1 \\ 2 & 2 & \cdots & 2 \\ \vdots & \vdots & \ddots & \vdots \\ K & K & \cdots & K \end{bmatrix}\)。
但是没法变成 \(K / 2\) 的矩阵。
我们转一转，发现这样的矩阵也满足条件：\(\begin{bmatrix} 1 & 2 & 3 & \cdots & K \\ 2 & 3 & 4 & \cdots & 1 \\ 3 & 4 & 5 & \cdots & 2 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ K & 1 & 2 & \cdots & K - 1 \end{bmatrix}\)。
但是它还是 \(K \times K\) 的，不过我们可以考虑在里面塞进去一些新值。
比如，当 \(K = 4\) 的时候我们可以把一些 \(1\) 替换成 \(5\)：\(\begin{bmatrix} {\color{red}{1}} & 2 & 3 & 4 \\ 2 & 3 & 4 & {\color{blue}{5}} \\ 3 & 4 & {\color{red}{1}} & 2 \\ 4 & {\color{blue}{5}} & 2 & 3 \end{bmatrix}\)。
可以发现，因为用了对角线填充，所以仍然满足条件，十分巧妙。
同理把一些 \(2\) 换成 \(6\) 也是可以的，所以 \(N \times N\) 的矩阵可以填进 \(2 N\) 种数（前提是 \(N\) 是偶数）。
所以找到合适大小的偶数 \(N\)，满足 \(N \le K \le 2 N\) 就行了。
时间复杂度为 \(\mathcal O (K^2)\)，评测链接。
2020-05-06
agc038_e
详细题解请见：AtCoder Grand Contest 038 E: Gachapon，评测链接。
