IOI 2020 集训队作业胡扯「51, 100」
IOI 2020 集训队作业胡扯「1, 50」
IOI 2020 集训队作业胡扯「51, 100」(★)
IOI 2020 集训队作业胡扯「101, 150」
如果您点击了某个超链接,但是并没有发生任何变化,这意味着您可能需要在另外两章节中寻找对应内容。
表格
绿的表示主要没看题解,红的表示主要看了题解。
2020-01-15
agc020_e
等价于计算有多少个编码方式,解码后能得到 \(S\) 的子集。
假设长度为 \(n\) 的字符串 \(s\) 的答案为 \(f(s)\),则可以列出两种转移方式:
-
\(f(s) =_+ f(s[1 : n - 1]) \times (1 + s[n])\)。
表示:编码方式的最后一个字符为0或1,去掉这个字符后,前面的方案数即为 \(f(s[1 : n - 1])\)。
而当 \(s[n] = 0\) 时,最后的字符只能填0,有 \(1\) 种方案;否则可以填0或1,有 \(2\) 种方案。 -
\(f(s) =_+ f(s[1 : n - li]) \times f(\bigcap_{j = 1}^{i} s[n - lj + 1 : n - l(j - 1)])\)(\(i \ge 2\),\(l \ge 1\),\(li \le n\))。
表示:编码方式的最后一个字符为),也就是说最后一段是(\(t\)x\(i\)),枚举长度 \(l = |t|\) 和重复次数 \(i\)。
后面的 \(t\) 需要满足解码后是 \(s\) 中最后 \(i\) 段长度为 \(l\) 的子串的交的子集,也就是 \(\bigcap_{j = 1}^{i} s[n - lj + 1 : n - l(j - 1)]\) 的子集。
你可能会认为这样子时间复杂度太大,但是题解告诉我们,记忆化搜索后,有用的状态数是 \(\mathcal O (2^{|S| / 8} + {|S|}^3)\) 的。每个状态可以花 \(\mathcal O (n^2)\) 的时间进行转移,反正就是跑过了。
时间复杂度为 \(\mathcal O ({|S|}^2 2^{|S| / 8} + {|S|}^5)\),评测链接。
cf566C
注意到 \({|x|}^{1.5}\) 是下凸函数,也就是说每个位置都可以求出向最优解方向移动的倾向,也就是导数。
考虑点分树,从根开始利用导数的正负确定应该往哪个子树方向走,最多走 \(\log n\) 层。
不需要显式建出点分树。
时间复杂度为 \(\mathcal O (n \log n)\),评测链接。
2020-01-16
cf587F
这题和 cf547E 极其相似,那题是问 \(s_k\) 在 \(s_{l \sim r}\) 中的出现次数,这题是问 \(s_{l \sim r}\) 在 \(s_k\) 中的出现次数。
令 \(\displaystyle \sum_{i = 1}^{n} |s_i| = l\),有 \(l = \Omega (n)\)。
先建出 AC 自动机,然后考虑一下答案如何表示。
令 \(\mathrm{id}_{i, j}\) 为 \(s_i[1 : j]\) 在 AC 自动机上对应的节点。
特别地,\(\mathrm{id}_i = \mathrm{id}_{i, |s_i|}\) 为 \(s_i\) 在 AC 自动机上对应的节点。
则询问 \((l, r, k)\) 的答案可以表示为:
令 fail 树中的 \(\mathrm{id}_{l \sim r}\) 的子树的权值都加上 \(1\)(重复的加多次)。
则答案为 \(\mathrm{id}_{k, 1 \sim |s_k|}\) 的权值和。
还以为和 cf547E 一样能有简单做法,结果想了半天都没想到 \(\mathrm{polylog}\) 的做法,看了一下题解发现是根号的。
考虑根号分治,\(|s_k| \le T\) 的和 \(|s_k| > T\) 的询问分开处理。
对于 \(|s_k| > T\) 的串,这样的串不会超过 \(l / T\) 个,考虑对于每个串使用线性的时间处理:
先把 \(\mathrm{id}_{k, 1 \sim |s_k|}\) 的权值定为 \(1\),然后在 fail 树上做一遍子树和,求出每个点子树中的权值和。
然后对于关于 \(s_k\) 的所有询问,拆分左右端点并按升序排序,用一个指针扫过所有询问端点,并用 \(\mathrm{id}_i\) 的权值累加答案。
这一部分的时间复杂度为 \(\mathcal O (l^2 / T)\)。
对于 \(|s_k| \le T\) 的串,每个询问考虑用 \(\mathcal O (|s_k|)\) 的时间进行处理:
对于每个询问拆分左右端点并按升序排序,用一个指针扫过所有询问端点,每处理一个,就把 fail 树上 \(\mathrm{id}_i\) 的子树的权值都加上 \(1\)。
对于每个询问 \(s_k\),查询 \(\mathrm{id}_{k, 1 \sim |s_k|}\) 当前的权值并累加,就是该询问的答案。
子树加,单点查使用 DFS 序 + 分块实现(\(B = \sqrt{l}\)),这一部分的时间复杂度为 \(\mathcal O (n \sqrt{l} + qT)\)。
令 \(T = \Theta (l / \sqrt{q})\) 可以取得最佳时间复杂度。
时间复杂度为 \(\mathcal O (n \sqrt{l} + q + l \sqrt{q})\),评测链接。
2020-01-27
cf571E
记集合 \(\{a, a b, a b^2, a b^3, \ldots \}\) 为 \(\langle a, b \rangle\),特别地,记 \(\{a\}\) 为 \(\langle a, 1 \rangle\)。
考虑合并 \(\langle a, b \rangle\) 和 \(\langle c, d \rangle\),形成新的集合,可以证明这个集合也可以表示成等比数列形式。
令所有 \(n\) 个 \(a, b\) 中涉及到的质数的集合为 \(P\),则可以把 \(a, b, c, d\) 表示为 \(|P|\) 维向量(第 \(i\) 个分量的大小为第 \(i\) 个质数在数值的质因数分解中的幂次)。
也就是要解 \(\vec{a} + k_1 \vec{b} = \vec{c} + k_2 \vec{d}\),其中 \(k_1, k_2\) 是非负整数。
考虑 \(\vec{b}\) 和 \(\vec{d}\) 是否为零向量,以及是否线性相关。
如果至少一个为零向量,可以直接判断,如果不线性相关,可以解二元一次方程组,如果线性相关,需要解线性同余方程。
大分类讨论即可。
时间复杂度为 \(\mathcal O (n^2 \omega(v) \log v)\),其中 \(v\) 是值域,\(\omega(n)\) 表示小于等于 \(n\) 的正整数的不同质因数个数的最大值,评测链接。
2020-01-28
cf590E
学习了一下偏序集上的最长反链求法。
令 \(l\) 为字符串长度之和。
先构造 AC 自动机,然后可以在 \(\mathcal O (l)\) 的时间内求出每个串在每个结束位置包含的最长的小串是哪一个。
注意这并不是全部的包含关系,所以还要用 Floyd 求出传递闭包,用 bitset 优化。
然后是偏序集上求最长反链(求方案),参考 [CTSC2008]祭祀river 的做法。
代码中使用了 Dinic 求二分图匹配。
时间复杂度为 \(\displaystyle \mathcal O \!\left( l + \frac{n^3}{w} + n^{2.5} \right)\),其中 \(w\) 为字长,评测链接。
2020-01-29
agc028_c
与其设置 \(x \to y\) 这条边的权值为 \(\min(A_x, B_y)\),我们看成有两条边,权值分别为 \(A_x\) 和 \(B_y\)。这样转化后,答案仍然相同。
我们考虑某种最终答案,假设走了 \(x \to y\) 这条边,
如果走的是权值为 \(A_x\) 的边,我们把这条边染红色,
如果走的是权值为 \(B_y\) 的边,我们把这条边染蓝色。
也就是说,红色边的边权等于它的起点的 \(A_x\),蓝色边的边权等于它的终点的 \(B_y\)。
我们考虑最终的答案形成的环,要么全是红边,要么全是蓝边,要么红蓝交替。
这不是废话吗?为什么要分三类?
这是因为只有红蓝交替,才能够允许同时存在「入边和出边都是红色的点」和「入边和出边都是蓝色的点」。
也就是说,当且仅当红蓝交替时,才能任意选入边和出边的颜色,如果不是红蓝交替的,则颜色必须完全一样。
那么我们先让答案变成全选红色和全选蓝色的 \(\min\),也就是 \(\sum A_i\) 和 \(\sum B_i\) 的 \(\min\)。
然后考虑红蓝交替时的答案怎么计算:
因为红蓝交替时,必然会出现入边为蓝色,出边为红色的点。我们枚举这样的一个点 \(i\) 之后,把它的 \(A_i\) 和 \(B_i\) 都加进答案,只要在剩余的 \(2n - 2\) 个 \(A_j\) 和 \(B_j\) 中,选出最小的 \(n - 2\) 个,就一定能够组成合法的答案。
把标号和权值一起记下来排序,就能得到每个点的 \(A_i\) 和 \(B_i\) 的排名,分类讨论一下不难得到答案。
时间复杂度为 \(\mathcal O (n \log n)\),评测链接。
2020-01-30
arc097_f
我们的目标是把所有白点变黑。首先,特判掉没有白点,或者白点只有 \(1\) 个的情况。分别输出 \(0\) 和 \(1\)。
我们记 \({col}_i\) 为点 \(i\) 的颜色,如果点 \(i\) 为白色,则 \({col}_i = 1\),否则 \({col}_i = 0\)。
剩下的情况中,我们把包含所有白点的极小连通块抽离出来(可以通过不断删除黑色叶子实现)。
显然,这个连通块形成了有 \(\ge 2\) 个点的一棵树。令连通块中的点数为 \(num\)。
不难发现,最优解中,猫一定不会踏出这个连通块。
但是又必须经过连通块内的每个点(因为必须经过连通块里的所有叶子,连通块中的所有叶子都是白点)。
那么接下来,我们只考虑这个连通块,定义 \({deg}_i\) 为连通块中点 \(i\) 的度数(不考虑原树中的边)。
又有结论:猫不会经过一条边 \(\ge 3\) 次,也就是说只会经过 \(1\) 次或 \(2\) 次。
(这是因为多余的操作都可以简化成“改变当前点的颜色”的操作,一定不会更劣)
我们先假设:猫必须回到起点。
可以发现这时猫的起点对答案已经没有影响了。因为每条边都会被正向反向分别经过恰好 \(1\) 次。
也就是说,先规划好了路线,计算这个路线对点颜色的影响。在这之后再“插入”改变当前点颜色的操作。
那么显然,在这个情况下,如果 \({deg}_i\) 为奇数,则 \({col}_i\) 就会因为该点被到达了奇数次而发生改变,否则 \({col}_i\) 保持不变。
最终,答案就等于 \(2 \cdot (num - 1) + \sum {col}_i\),也就是 \(2\) 乘边数,加上 \({col}_i = 1\) 的点数,这些点需要额外使用一次操作。
问题在于:猫不一定要回到起点。
假设猫从 \(x\) 出发,最终到达了 \(y\)。令 \(x\) 与 \(y\) 之间的边数为 \(len\)。
则可以少走 \(len\) 条边,也就是不用从 \(y\) 再返回 \(x\) 了。
但是少走的这 \(len\) 条边,对 \(col\) 也有影响:
因为从 \(y\) 返回 \(x\) 的边少走了,所以 \(x\) 到 \(y\) 路径上的点(除了 \(y\) 本身)的 \(col\) 都会发生变化。
实际上恰好有 \(len\) 个点的 \(col\) 发生了变化。
如果 \(col\) 从 \(1\) 变成了 \(0\),可以少花一次操作。但是从 \(0\) 变成 \(1\) 的话,就要多花一次操作。
也就是说,平均算下来,如果原先的 \(col\) 是 \(1\),可以少花两次操作;如果是 \(0\),则不亏不赚。
总的来说,就是这条路径,经过的 \({col}_i = 1\) 的点要尽量多(但是不包含终点)。
一个观察:叶子的 \(col\) 始终为 \(0\)(因为原先叶子的 \(col = 1\),但是叶子的 \(deg\) 也是 \(1\),所以抵消了)。
而这条路径自然是越长越好,肯定会延伸到叶子,所以包不包含终点也没有影响了。
树形 DP 计算经过的 \({col}_i = 1\) 的点最多的路径就行了。
假设最多经过 \(ans\) 个 \({col}_i = 1\) 的点,则最终答案为 \(2 \cdot (num - 1) + \sum {col}_i - 2 \cdot ans\)。
时间复杂度为 \(\mathcal O (n)\),评测链接。
agc030_d
因为 \(N\) 很小,考虑直接枚举位置对 \(\langle i, j \rangle\)(\(1 \le i < j \le N\))以统计逆序对。
考虑一个概率 DP:令 \(f(i, j)\)(\(1 \le i, j \le N\))为当前时刻下,\(A_i > A_j\) 的概率。
(这里假设对于 \(Q\) 个操作,每个操作都以 \(1 / 2\) 的概率执行)
那么最终时刻下,满足 \(i < j\) 的 \(f(i, j)\) 之和,再乘以 \(2^Q\) 就是答案(期望的线性性)。
按顺序考虑每个时刻(操作),考虑新的 \(f(i, j)\) 和原先的比有什么变化。
可以发现只有 \(\mathcal O (N)\) 个位置会发生变化。具体地说,只有 \(i, j\) 有至少一个等于 \(X_i\) 或 \(Y_i\) 时才有可能发生变化。
暴力转移即可。
时间复杂度为 \(\mathcal O (N (N + Q))\),评测链接。
arc093_e
考虑原图的一棵生成树 \(T\),边权和为 \(S\)。
对于一条非树边 \(e\),定义 \(v(e)\) 为 \(W_e\) 减去「\(U_e, V_e\) 在 \(T\) 上的路径上的最大边权」。
也就是说,\(v(e)\) 表示用 \(e\) 替换 \(T\) 中的一条边,形成新的生成树的最小代价。显然有 \(v(e) \ge 0\)。
假设染色方案已确定,如何计算满足条件的最小生成树?
- 如果 \(T\) 中的边不同色,则 \(T\) 就是合法的最小生成树,权值为 \(S\)。
- 否则 \(T\) 中的边都是同一种颜色,取 \(v(e)\) 最小的异色的 \(e\),则合法的最小生成树的权值为 \(S + v(e)\)。
- 如果不存在这样的 \(e\)(所有边全部同色),则不存在合法的生成树。
那么答案就很显然了,先把 \(X\) 减去 \(S\)。
如果 \(X < 0\),则无合法解,输出 0。
如果 \(X > 0\),则 \(T\) 必须同色,且 \(v(e) < X\) 的边都必须染相同颜色,\(v(e) = X\) 的边必须至少有一个染不同颜色。
如果 \(X = 0\),则是上面的答案的基础上,再加上 \(T\) 不同色,其它边任意选的方案数。
容斥一下答案就出来了。
时间复杂度为 \(\mathcal O (M \log M)\),评测链接。
2020-02-01
agc024_d
观察样例,再自己手造几组数据,就可以发现,最终长成的树必然是:
- 以一个点为中心的放射状。
- 以一条边为中心的放射状(两侧对称)。
更具体地说,也就是把中心点或中心边「拎起来」,下面挂着的树形态,满足每个深度相同的子树都完全一致。
而这时,答案就为树的深度(假设中心点的深度为 \(1\),中心边的两端点深度为 \(1\))。
而叶子个数,就等于每一个深度的节点的,子节点个数的乘积(包括深度 \(1\),但不包括叶子所在的深度)。
那么我们枚举中心点,或者中心边,把原树「拎起来」,原树就变成了一个奇怪的形状。
那么显然我们需要补最少的点,对于每个深度,把子节点个数取 \(\max\) 再相乘,就得到最终的最少叶子个数了。
每个点和边都枚举一遍,取最优解。
时间复杂度为 \(\mathcal O (n^2)\),评测链接。
arc091_f
这题真的好简单……
显然我们求一下每堆石子的 SG 函数就好了。
我们打表找规律,当 \(K = 1\) 的时候,就是普通的 Nim。如果 \(K \ge 2\) 会怎么样?
以 \(K = 4\) 为例:
不难发现规律:
然而直接这样算有点慢,不难发现,如果按照 \(\displaystyle \left\lfloor \frac{n}{k} \right\rfloor\) 分段,则每一段内是循环的。
可以把第三行改写成:\(\displaystyle \operatorname{SG}_k \!\left( n - \!\left\lfloor \frac{\displaystyle n - \!\left\lfloor \frac{n}{k} \right\rfloor\! \cdot (k - 1)}{\displaystyle \left\lfloor \frac{n}{k} \right\rfloor\! + 1} \right\rfloor\! \cdot \!\left( \left\lfloor \frac{n}{k} \right\rfloor\! + 1 \right) \right)\)。
这样子计算,可以证明会在 \(\sqrt{n}\) 次内结束。
时间复杂度为 \(\mathcal O (N \sqrt{A})\),评测链接。
2020-02-02
agc035_c
当 \(N\) 是 \(2\) 的次幂时无解,这是因为 \(N\) 的最高位无法被异或得到。
否则一定有解,构造如下(令 \(m\) 为小于等于 \(N\) 的最大的 \(2\) 的次幂,\(k\) 为 \(N - m\)):
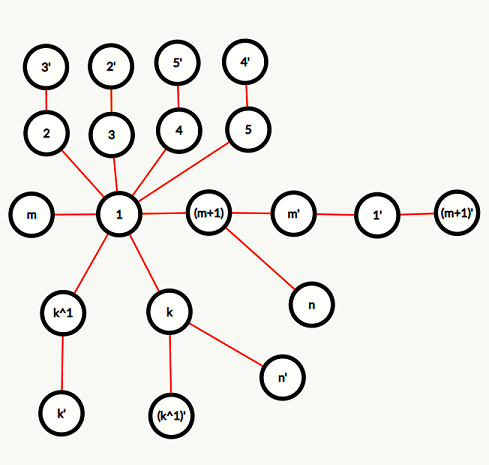
当 \(N\) 是偶数时才需要连 \((m+1) \leftrightarrow N\) 和 \(k \leftrightarrow N'\)。
时间复杂度为 \(\mathcal O (N)\),评测链接。
2020-02-03
cf603E
考虑给定了边集后,如何判断是否存在合法的选边方案。
容易证明存在一种方案,当且仅当每个连通块的大小都是偶数。
(考虑每个连通块仅保留一棵生成树,再在生成树上自底向上选边)
所以先把 \(n \bmod 2 \ne 0\) 的情况判掉(全部输出 -1)。
那么相当于每次我们可以尝试不断把权值最大的边删去,使得删去后图的每个连通块大小仍为偶数。
加边删边时,使用 LCT 维护最小生成树即可。
判断一条边是否需要删除,需要用能够统计虚子树信息的 LCT,这里虚子树信息就是子树大小。
为了方便考虑,代码中在初始的时候就加上了 \(n / 2\) 条边,第 \(i\) 条连接 \(2i - 1\) 和 \(2i\),权值为 \(\infty\)。
这样做可以保证在一开始的时候每个连通块大小都是偶数,省去了不必要的特判,如果算出来答案为 \(\infty\),就输出 -1。
时间复杂度为 \(\mathcal O (m \log m)\),评测链接。
2020-02-04
agc034_e
既然所有棋子最终到达了同一个点,我们先考虑枚举这个点,记做 \(r\),以 \(r\) 为根建树。
记 \(s_i\) 表示 \(i\) 子树中的所有点 \(A_i\) 之和,也就是子树中的棋子个数;
记 \(w_i\) 表示 \(i\) 子树中的所有棋子到 \(i\) 的距离之和。
这样,\(s_i\) 和 \(w_i\) 都可以很容易地计算。
(具体地说,\(\displaystyle w_u = \sum_{v \in \mathrm{sons}_u} w_v + s_v\))
考虑做题目中的操作会带来的影响,假设操作的棋子分别位于 \(x, y\):
- \(x, y\) 为祖孙关系。这个操作对 \(r\) 本身,以及 \(r\) 的任意一个子树方向的 \(w\) 值都不会产生影响(注意不是子树,而是这个子树对 \(w_r\) 产生的贡献)。
- \(x, y\) 在 \(r\) 的不同子树中。这个操作会使 \(r\) 的那两个子树方向的 \(w\) 值各减去 \(1\)。
- \(x, y\) 在 \(r\) 的同一个子树中,但是不为祖孙关系。这个操作会使 \(r\) 的那一个子树方向的 \(w\) 值减去 \(2\)。
可以发现:如果 \(w_r\) 为偶数,在所有子树方向的贡献中,最大的那一个,也不超过 \(w_r\) 的一半的话,就可以不断通过 2 操作把某两个子树方向的贡献减去 \(1\),最终使得 \(w_r\) 变成 \(0\)。也就意味着所有棋子都到达了 \(r\)。(具体方法是,每次都选择当前贡献最大的子树中的一个棋子进行操作)
但是如果贡献最大的那个子树,它的贡献超过了 \(w_r\) 的一半怎么办呢?这时就需要在这个子树中使用 3 操作以减小这个子树的贡献。可以发现这个贡献减得越小越好。
这启发我们定义 \(f_i\) 表示只操作 \(i\) 子树中的棋子,能够把 \(w_i\) 最小减少到多少。就是做操作后 \(w_i\) 的最小值。
这样一来,只要 \(f_r = 0\),就意味着可以把棋子都聚集到 \(r\) 上,且根据上面的过程,恰好花费 \(w_r / 2\) 步。
(因为没必要使用 1 操作,而 2, 3 操作都会让 \(w_r\) 减去 \(2\))
我们考虑递归地计算 \(f_i\)。要求 \(f_u\) 时,考虑 \(u\) 的每个子节点 \(v\) 的 \(w_v\) 和 \(f_v\)。
同样地,考虑对 \(w_u\) 贡献最大的那个子树 \(v\),我们使用 3 操作,让它的 \(w_v\) 变成了 \(f_v\)。
这样一来,若 \((f_v + s_v) \le w_u / 2\),则 \(f_u = w_u \bmod 2\),否则 \(f_u = (f_v + s_v) - (w_u - (w_v + s_v))\)。
这样就可以在 \(\mathcal O (N)\) 的时间内计算最终聚集到点 \(r\) 的答案了。总时间复杂度为 \(\mathcal O (N^2)\),足以通过该题。
显然这个式子是可以换根 DP 的,所以代码中也就写了,时间复杂度变为 \(\mathcal O (N)\)。
时间复杂度为 \(\mathcal O (N)\),评测链接。
agc026_d
去年 CSP 前,做过一个比赛,出题人搬了这题,我打了一整场比赛把它切掉了,其他题没分(
PS:数据范围改成了 \(1 \le N \le {10}^5\)。
注意:我的做法与题解的做法有较大出入。
我们首先考虑这样的 DP:令 \(dp(i)\) 表示前 \(i\) 列已经染色,其他列还未染色的方案数。
但是这样定义的状态是没法转移的。
为什么?我们先考虑一下转移的方式:
- 如果相邻的两个格子为同种颜色(
##或##或竖着排列的),则它们所在的 \(2 \times 2\) 区域中的颜色将被唯一确定。
即##或
####或它们旋转 \({90}^{\circ}\) 的结果。
## - 如果相邻的两个格子的颜色不同(
##或##或竖着排列的),在不考虑其它限制的情况下,它们所在的 \(2 \times 2\) 区域中的颜色是有两种方案的。
即##或其旋转 \({90}^{\circ}\) 的结果。
##
现在,考虑前 \(i - 1\) 列已经染色,第 \(i\) 列以及之后还未染色的情况。
那么第 \(i\) 列的染色情况,可以只由第 \(i - 1\) 列的染色情况确定。
下面举几个例子(假设第一列为第 \(i - 1\) 列,第二列为第 \(i\) 列):
?,这个情况下第 \(i\) 列有 \(8\) 种染色方案:最底下 \(6\) 行 \(2\) 种,上面两个格子 \(2 \times 2 = 4\) 种。
?
#?
#?
#?
#?
#?
#?
?,这个情况下第 \(i\) 列有 \(4\) 种染色方案:最底下 \(6\) 行 \(1\) 种,上面两个格子 \(2 \times 2 = 4\) 种。
?
#?
#?
#?
#?
#?
#?
#,这个情况下第 \(i\) 列有 \(2\) 种染色方案。
#
#?
#?
#?
#?
#?
#?
#,这个情况下第 \(i\) 列有 \(1\) 种染色方案。
#
#?
#?
#?
#?
#?
#?
可以发现,关键就在于第 \(i - 1\) 列的,最靠下的,上下相邻两个格子颜色相同的位置。
如果这个位置在第 \(i\) 列的范围内,则第 \(i\) 列的最底下 \(\min(h_{i - 1}, h_i)\) 个格子的颜色就会被唯一确定,否则恰有两种方案。
剩下 \(\max(h_i - h_{i - 1}, 0)\) 个格子可以任意染色。
可能可以考虑记状态 \(dp(i, j)\) 表示前 \(i\) 列已经染色,且第 \(i\) 列最靠下的上下相邻两个格子颜色相同的位置为 \(j\)。
但是这样状态也太多了,也没法做。
最后我们考虑记状态 \(dp(i)\) 表示:前 \(i\) 列已经染色,且保证第 \(i\) 列任意两个相邻格子的颜色都不同的方案数。
也就是第 \(i\) 列颜色红蓝交错的方案数。这样令 \(h_{n + 1} = 1\),则 \(dp(n + 1) / 2\) 就是答案。
我们考虑转移,如果 \(h_{i - 1} \le h_i\),也就是第 \(i\) 列变高了,则 \(dp(i) = 2 \cdot dp(i - 1)\)。
这是因为我们限制了第 \(i\) 列是红蓝交错的,又因为 \(h_{i - 1} \le h_i\),所以第 \(i - 1\) 列也必然是红蓝交错的,可以直接转移。
但是如果 \(h_{i - 1} > h_i\) 怎么办?这时限制第 \(i\) 列红蓝交错,不能保证第 \(i - 1\) 列也是红蓝交错的。
先小结一下:可以发现,如果第 \(x\) 列的最底下 \(w\) 个格子是红蓝交错的,那么对于 \(y = x - 1\) 或 \(x + 1\),也就是 \(x\) 的相邻列,可以推出第 \(y\) 列的最底下 \(\min(w, h_y)\) 个格子是红蓝交错的。
这引出一个结论:如果第 \(x\) 列是红蓝交错的,则第 \(y\) 列是红蓝交错的充分条件是:对于 \(x \le i \le y\) 有 \(h_i \ge h_y\)。
换句话说,就是 \(h_y\) 是 \(x, y\) 之间(包含 \(x, y\))的 \(h\) 的最小值。
回到 DP 上,仍然是要转移 \(dp(i)\),我们假设前一个一整列都是红蓝交错的列为第 \(j\) 列。
则这个 \(j\) 要满足 \(\displaystyle h_j < \min_{j < k < i} h_k\),且「\(h_j \ge h_i\) 或『\(h_j < h_i\) 且 \(\displaystyle \min_{j < k < i} > h_i\)』」。
这等价于 \(j\) 是前 \(i - 1\) 列单调栈中的元素(我们维护 \(h\) 值严格递增的单调栈),且当加入 \(i\) 时 \(j\) 被弹栈或 \(j\) 为弹栈后的栈顶(但不能弹出 \(h\) 值恰好等于 \(h_i\) 的元素)。
根据单调栈的结论,总转移数是 \(\mathcal O (N)\) 的,这是可以接受的。接下来要考虑转移的系数。
我们首先考虑第一类转移,也就是 \(j\) 为被弹栈的元素(\(h_j \ge h_i\))的转移:
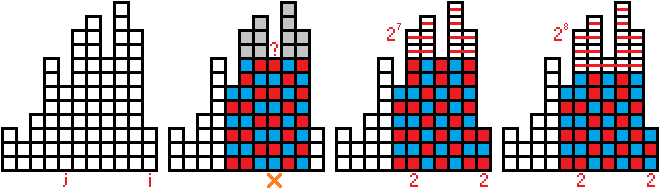
我们考虑上图,\(j = 5\),\(i = 11\)。
\(j\) 到 \(i\) 之间的 \(h\) 值依次为 \(6, 10, 11, 8, 12, 10, 3\)。
我们已知第 \(j\) 列是红蓝交错的,而之后的每一列都必须不是红蓝交错的。
如果出现了类似图二中的情况,也就是在“中间部分”(不包括 \(j\) 和 \(i\) 的部分)出现了相邻两列颜色没有翻转的话,就会导致“中间部分”出现一整列都是红蓝交错的情况,不符合要求。
也就是说“中间部分”必须满足:每一列的颜色都和上一列的不同,除了最初的那一列(第 \(j + 1\) 列)。
又因为第 \(i\) 列的颜色也可以选择翻转或不翻转,所以这里总共贡献了 \(2^2 = 4\) 的系数。
考虑图三和图四的上面的部分,因为不能让第 \(8\) 列出现一整列都是红蓝交错的情况,需要存在一行的颜色不翻转,这里有 \(2\) 种情况。
而更上面未染色的部分,每一段红色的线条都会产生 \(2\) 的贡献(可以选择翻转或不翻转)。
为什么有恰好 \(2\) 种情况呢?这是因为 \(h_8 - h_j = 8 - 6 = 2\)。
这一部分的总贡献为 \(2^7 + 2^8\),实际上是一个等比数列的形式。
这个等比数列的首项为 \(2^{\mathrm{num1}}\),末项为 \(2^{\mathrm{num2} - 1}\)。总和就为 \(2^{\mathrm{num2}} - 2^{\mathrm{num1}}\)。
这里就有 \(\mathrm{num2} = 9\),以及 \(\mathrm{num1} = 7\)。
而 \(\mathrm{num1}, \mathrm{num2}\) 如何计算呢?
我们记 \(b_i\) 表示前 \(i\) 列的形如这样的红线个数。可以发现 \(\mathrm{num2} = b_{i - 1} - b_j\),而 \(\mathrm{num1} = \mathrm{num2} - (h_k - h_j)\)。
其中 \(k\) 就为上一个被弹栈的元素(这里 \(k = 8\)),也就是满足 \(j < k\) 的 \(h_k\) 最小的元素之一。
综上所述,\(j\) 对 \(i\) 产生的贡献就为 \(4 (2^{\mathrm{num2}} - 2^{\mathrm{num1}})\) 倍的 \(dp(j)\)。
(特殊情况是 \(j = i - 1\),因为“中间部分”完全消失了,所以不能套用上面的推导,这时贡献为 \(2\))
然后我们考虑第二类转移,也就是 \(j\) 为弹栈后的栈顶,且上一个被弹栈的元素的 \(h\) 值不等于 \(h_i\):

仍然是 \(i = 11\) 的情况,此时 \(j = 2\)。
如图二,同样地我们不能允许出现在“中间部分”的相邻两列颜色不翻转的情况。
特别地,如图三,我们需要的红蓝交错的高度不是 \(h_j\) 而是 \(h_i\),因为 \(h_i > h_j\)。
如图四,可以发现此时颜色不翻转的行,只有 \(1\) 种取值了,也就是 \(h_3 - h_i = 4 - 3 = 1\)。
而上面的部分仍然和前一种情况类似,我们可以求出此时的 \(\mathrm{num2} = b_{i - 1} - b_j - (h_i - h_j)\),而 \(\mathrm{num1} = \mathrm{num2} - (h_k - h_i)\)。
其中 \(k\) 的含义和前文相同,为上一个被弹栈的元素。
综上所述,\(j\) 对 \(i\) 产生的贡献就为 \(4 (2^{\mathrm{num2}} - 2^{\mathrm{num1}})\) 倍的 \(dp(j)\)。
(特殊情况是 \(j = i - 1\),因为“中间部分”完全消失了,所以不能套用上面的推导,这时贡献为 \(2\))
然而其实我们漏掉了一种情况,要是这样的 \(j\) 不存在呢?也就是不存在红蓝交错的前一列该怎么办?
其实这无关紧要,我们只要让 \(h_0 = 1\),然后设 \(dp(0) = 1\) 就行了,不影响后续计算。
时间复杂度为 \(\mathcal O (N \log \mathrm{MOD})\),其中 \(\log \mathrm{MOD}\) 为快速幂复杂度,评测链接。
2020-02-05
arc103_d
令值域为 \(v\),本题中 \(v = {10}^9\)。
每次操作,你必须让 \(x\) 坐标或 \(y\) 坐标增加或减少一个定值 \(d\)。
令一个点 \((x, y)\) 的奇偶性为 \((x + y) \bmod 2\),可以发现能够操作到的点的奇偶性都相同,所以先把无解判掉。
好像没有什么特别的构造方法。我们先考虑二进制拆分。
但是搞了半天之后,发现二进制拆分好像只能做到 \(2 (\lfloor \log_2 v \rfloor + 1)\) 次操作。
然后我们惊奇地发现,\(2 (\lfloor \log_3 v \rfloor + 2)\) 好像恰好就是 \(40\) 啊。
所以我们考虑把坐标表示成三进制数,注意这里三进制的系数,应该是 \(0, 1, -1\) 三种。
那么我们令 \(m = 40\),\(d_1 \sim d_m\) 分别为 \(1, 1, 3, 3, 9, 9, 27, 27, 81, 81, \ldots\)。
也就是对于每一个 \(0 \le i \le 19\),\(3^i\) 在 \(d\) 中出现两次。
(如果所有点的奇偶性为 \(1\),则去掉一个 \(3^{19}\))
接下来构造解,每一位使用恰好两个 \(3^i\):
我们从低位到高位考虑,假设考虑到了第 \(k\) 位。记 \(x_k, y_k\) 分别表示 \(x, y\) 坐标第 \(k\) 位的值。
- \(x_k = 0, y_k = 0\):
做RL操作,也就是让 \(x\) 减去 \(1\) 再加上 \(1\),也就是不变。 - \(x_k \ne 0, y_k \ne 0\):
做R/L操作中的一个,让 \(x_k\) 变成 \(0\);
做U/D操作中的一个,让 \(y_k\) 变成 \(0\)。 - \(x_k \ne 0, y_k = 0\):
如果 \(x_k = 1\),做LL操作,让 \(x_k\) 变成 \(3\);
如果 \(x_k = -1\),做RR操作,让 \(x_k\) 变成 \(-3\);
无论是哪种操作都需要进/借位,最后 \(x_k\) 还是变成了 \(0\)。 - \(x_k = 0, y_k \ne 0\):
类似上一种情况。
特别地,如果考虑到了第 \(k = 19\) 位:
- 点的奇偶性为 \(0\):只会出现上述情况中的 1, 2 两种。
- 点的奇偶性为 \(1\):只剩一个 \(3^{19}\) 了,\(x_k, y_k\) 也必然只有一个非 \(0\),做
R/L/U/D操作中的一个即可。
因为 \(\lfloor \log_3 v \rfloor = 18\),所以可以证明在执行上述操作时,只会影响到第 \(0 \sim 19\) 位。
时间复杂度为 \(\mathcal O (N \log_3 v)\),评测链接。
看了题解后发现我是睿智,可以用二进制的,而且只需要 \(32\) 次。
2020-02-06
cf553E
令 \(f(i, k)\) 为第 \(i\) 个点在 \(k\) 时刻,最佳策略下到达终点的代价期望值;类似定义 \(g(j, k)\) 表示第 \(j\) 条边的代价期望值。
则 \(f\) 和 \(g\) 互相转移,以 \(k\) 为阶段可以发现都是从大往小转移。最终答案就是 \(f(1, 0)\)。
固定 \(f(i, \ast)\) 和 \(g(j, \ast)\),转移形式是一个卷积,用分治 FFT 优化即可。
一开始的边界条件要先跑一下最短路。
时间复杂度为 \(\mathcal O (n^3 + m t \log^2 t)\),评测链接。
agc022_e
这道题挺神的,我尝试用比较好理解的方式解释一下:
我们考虑判断一个已知的串是否合法。
首先一个显然的事实:假设我们把串的某一位从 0 变成了 1,那么一定是变优了,反之一定是变劣了。
也就是说,单独修改某一位的优劣性,是可以简单判断的。
接下来我们列举一些操作的情况:
11a => 1
10a => a
01a => a
00a => 0
1ab => (a|b)
0ab => (a&b)
又有一结论:如果 \(S\) 形如 11...,那么一定合法,这是因为,只要把后面的部分缩起来,再缩 11a 得到 1 即可。
我们再考虑串形如 00... 时,因为迟早要对 00 进行操作,我们不妨直接考虑对 00 进行操作时:
假设串形如 00ab...,那么操作 00a 得到 0b...,操作 0ab 得到 0(a&b)...。
显然前者不劣于后者,所以直接操作前者即可。也就是说 00a... == 0...。
考虑串形如 01... 时,同样地,直接考虑对 01 进行操作时:
假设串形如 01ab...,那么操作 01a 得到 ab...,操作 1ab 得到 0(a|b)...。
当 a=0 或 b=1 时,前者不劣于后者。当 a=1 且 b=0 时,两种操作分别得到 10... 和 01...。
到底是 10... 优还是 01... 优呢?这里我们先不作解答。
考虑串形如 10... 时:
假设串形如 10ab...,那么操作 10a 得到 ab...,操作 0ab 得到 1(a&b)...。
当 a=1 时,前者不劣于后者。当 a=0 且 b=0 时,后者不劣于前者。当 a=0 且 b=1 时,两种操作分别得到 01... 和 10...。
又回到了比较 10... 和 01... 的问题上。
我们考虑 10xy... 和 01xy...:
- 如果 x=0,则前者可以得到 0y... 或 10...;而后者可以得到 0y...。
此时,前者不劣于后者。 - 如果 x=1,则前者可以得到 1y...;而后者可以得到 1y... 或 01...。
如果 y=1,前者不劣于后者。
如果 y=0,两者都能得到 10...,而后者还可以得到 01...。
但是不能无限地往后接 10 循环,最终一定会变成 10a 或 01a,但是它们的结果确实是相同的,没有孰优孰劣。
所以结论是 10... 比 01... 更优。
一个例子是:10001 和 01001,前者是合法的串,而后者不是。
那么我们构造如下转移图:
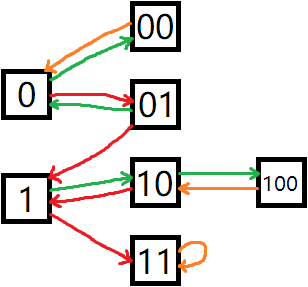
其中绿边表示 \(0\) 的转移,红边表示 \(1\) 的转移,橙边表示 \(0, 1\) 都是这个转移。
然后在这个自动机上转移即可。最终答案为 1 和 11 上的方案数之和。
时间复杂度为 \(\mathcal O (|S|)\),评测链接。
arc101_e
直接 DP 的话大概是 \(\mathcal O (N^3)\) 的,使用容斥原理:
要计算的就是 \(\displaystyle \sum_{S \subseteq E} {(-1)}^{|S|} f(S)\),其中 \(f(S)\) 表示强制不能覆盖到 \(S\) 中的边的方案数。
也就是把 \(S\) 内的边都删掉,原树被分割成了若干连通块,每个连通块内部连线的方案数。
显然一个大小为 \(n\) 的连通块,任意连线的方案数为 \(1 \cdot 3 \cdot 5 \cdot \cdots \cdot (n - 1)\)(如果 \(n\) 是偶数,\(n\) 是奇数的话显然没有方案)。
那么设状态 \(dp(i, j)\) 表示考虑 \(i\) 的子树,割掉若干条边,\(i\) 所在的连通块大小为 \(j\),的贡献总和(不算 \(i\) 所在连通块的贡献)。
转移也是显然的。
时间复杂度为 \(\mathcal O (N^2)\),评测链接。
arc101_f
首先,每个机器人只会从它旁边的两个出口离开。
对于旁边只有一个出口的机器人,直接不管它就行,不会影响答案。
对于旁边有两个出口的机器人,我们只需要保存它到两个出口之间的距离。
上述处理都可以通过双指针来完成。
现在问题就变成了,给定 \(k\)(\(0 \le k \le N\))个机器人,第 \(i\) 机器人到它左边和右边的出口的距离分别为 \(x_i\) 和 \(y_i\)。
我们把每个机器人画在坐标系中,第 \(i\) 个机器人的位置就是 \((x_i, y_i)\)。
可以发现,相当于我们操控两条直线,初始时这两条直线的位置分别为 \(x = 0\) 和 \(y = 0\),也就是在坐标轴上。
我们可以把竖线往右移动,把横线往上移动。如果线碰到了一个点,这个点就被这条线吃掉,然后消失。
问点被线吃掉的,不同的方案数。
我们考虑这两条线的交点形成的轨迹,可以发现,在轨迹上方的点是被竖线吃掉的,在轨迹下方的点是被横线吃掉的。
那么我们考虑统计这条轨迹穿过这些点的方案数。限制是轨迹必须是增函数。
我们把坐标离散化一下,用树状数组优化 DP 就可以做了。
具体地说,我们把所有点按照横坐标递增排序。然后考虑某条竖线上的点如何转移。
令 \(dp(i, j)\) 表示,考虑了横坐标 \(\le i\) 的点了,并且轨迹下的点的纵坐标最大值为 \(j\) 的方案数。
则 \(dp(i, j)\) 可以转移到 \(dp(i + 1, j)\) 和 \(dp(i + 1, y)\)(存在点 \((i + 1, y)\) 满足 \(y > j\))。
用树状数组维护。
时间复杂度为 \(\mathcal O (M + N \log N)\),评测链接。
2020-02-07
arc103_f
假设满足条件的树为 \(T\),我们考虑 \(T\) 的一些性质。
首先 \(T\) 只有一个重心,因为如果有两个,那么它们两个的 \(D\) 值就应该相同,与题意矛盾。
显然重心就是 \(D\) 值最小的那个点。
令 \(T\) 以重心为根,容易发现,任何一个非根节点的 \(D\) 值都大于它的双亲节点的 \(D\) 值。
我们选取 \(D\) 最大的那个点 \(u\),显然它必须是叶子。
我们可以计算出它的双亲节点的 \(D\) 值应该恰好为 \(D_u - N + 2 \cdot \mathrm{siz}\),其中 \(\mathrm{siz}\) 为 \(u\) 的子树大小(此时为 \(1\))。
那么就可以唯一确定它的双亲节点是哪一个。
然后把该点“删去”,并让它的双亲节点的 \(\mathrm{siz}\) 加上 \(1\)。
重复 \(n - 1\) 次这个过程。就可以确定出 \(T\) 的形态。
也就是说,满足条件的 \(T\) 其实是唯一的。
这时我们再 DFS 检查一下是否确实满足条件即可。
时间复杂度为 \(\mathcal O (N \log N)\),评测链接。
agc020_d
首先我们可以得出:最短的连续段长度等于 \(\displaystyle \left\lceil \frac{\max\{A, B\}}{\min\{A, B\} + 1} \right\rceil\! = \!\left\lfloor \frac{A + B}{\min\{A, B\} + 1} \right\rfloor\),令这个值为 \(K\)。
观察 \(A \ge B\) 的情况(留作练习,请读者自行完成)(大雾)
可以发现,一组 \(A, B\) 的答案,就是当 \(A = (B + 1) K\) 时的答案(形如 \([B \cdot (K \cdot \texttt{"A"} + \texttt{"B"}) + K \cdot \texttt{"A"}]\)),
去掉靠后的恰好 \((B + 1) K - A\) 个 \(\texttt{"A"}\) 得到的,令这个值为 \(\mathrm{del}\)。
但是并不一定是去掉最后 \(\mathrm{del}\) 个 \(\texttt{"A"}\),考虑 \(A = 8, B = 6\) 的情况:\(\texttt{"AABAABAABABABB"}\)。
它就是 \(A = 14, B = 6\) 的情况:\(\texttt{"AABAABAABAABAABAABAA"}\) 去掉 \(6\) 个 \(\texttt{"A"}\) 得到的,但是不是最后 \(6\) 个。
这是因为如果去掉了最后 \(6\) 个,就会有 \(3\) 个 \(\texttt{"B"}\) 形成连续段,与「连续段长度不大于 \(2\)」冲突。
也就是说,贪心地去掉尽可能靠后的 \(\mathrm{del}\) 个 \(\texttt{"A"}\),但是不形成 \((K + 1) \cdot \texttt{"B"}\) 的连续段。
讨论一下就可以得到结果了。
对于 \(A < B\) 的情况类似,是 \(B = (A + 1) K\) 时的答案(形如 \([A \cdot (K \cdot \texttt{"B"} + \texttt{"A"}) + K \cdot \texttt{"B"}]\)),
去掉尽可能靠前(不是靠后)的若干个 \(\texttt{"B"}\) 得到的,类似做就行了。
时间复杂度为 \(\mathcal O (Q (D - C + 1))\),评测链接。
2020-02-08
arc099_f
考虑记前缀和信息 \((\Lambda_i, \delta_i)\) 表示依次吃掉 \(1 \sim i\) 的所有字符后,得到的序列和指针 \(P\) 的位置。
那么两信息的合并:\((\Lambda_1, \delta_1) \circ (\Lambda_2, \delta_2) = (\Lambda_1 + \Lambda_2 \gg \delta_1, \delta_1 + \delta_2)\)。
我们记 \(h_i\) 为 \(\displaystyle \sum_{p} \Lambda_i[p] \beta^p\)。
则有 \((h_1, \delta_1) \circ (h_2, \delta_2) = (h_1 + h_2 \beta^{\delta_1}, \delta_1 + \delta_2)\)。
考虑 \(g = h_n\),一个区间 \([i, j]\) 的信息等于 \(g\) 当且仅当 \(h_{j - 1} + g \beta^{\delta_{j - 1}} = h_i\)。
那么我们从后往前枚举 \(j\),维护一个 \(h_i\) 的桶,以统计答案。
把 \(h\) 哈希一下就可以存进桶里了,为了防止冲突需要使用双哈希。
时间复杂度为 \(\mathcal O (N \cdot \mathcal T (\mathrm{hash}))\),评测链接。
agc031_d
根据题意,我们可以得到 \(a_i = a_{i - 1} {(a_{i - 2})}^{-1}\)。其中 \(q p\) 表示置换的复合,满足 \({(q p)}_i = q_{p_i}\)。
将 \(a_0\) 至 \(a_{11}\) 列出,可得:
所以是有个长度为 \(6\) 的循环节。
令 \(z = q p^{-1} q^{-1} p\),则 \(a_K\) 可以表示为 \(z^{K \div 6} a_{K \bmod 6} {(z^{-1})}^{K \div 6}\)。
时间复杂度为 \(\mathcal O (N \log K)\),评测链接。
cf587D
容易发现这是一个 2-SAT 的形式。
要求删除 \(t\) 尽量小的边,那就先二分答案。
不过还是要考虑建图的问题。
如果直接建图的话,会发现每个点周围的边都会互相影响,也就是删掉其中一条就不能删另一条。
直接建边的话要建 \(\mathcal O ({deg}^2)\) 条。
其实限制就是,一个点周围的边,最多删一条。
那么我们再在 2-SAT 模型中新建若干个变量,\(s_i\) 表示前 \(i\) 条边是否被删去。
如果 \(s_i = 1\),那么就有 \(s_{i + 1} = 1\),\(a_{i + 1} = 0\)。
如果 \(a_i = 1\),那么就有 \(s_i = 1\)。
大概是个链前缀和的形式。
这样子边数就是线性的了。
时间复杂度为 \(\mathcal O (m \log m + m \log t)\),评测链接。
cf674F
这里我就抄 CMXRYNP 的题解了。
从能够得到的信息考虑。
最多有 \(\min\{p, n - 1\}\) 只熊要去睡觉,我们先让 \(p\) 对 \(n - 1\) 取 \(\min\)。
那么对于每只熊,我们可以知道它有没有去睡觉,如果有可以知道它在第几晚去睡觉的。
所以最多的情况数就是:
也就是枚举 \(k\) 只熊去睡觉了,然后 \(i\) 是天数。
这是桶数量的一个上界。因为再怎么改变策略最后也只有这么多种情况。
我们可以证明这个上界是可以被达到的。
把所有情况编号,对于第 \(x\) 种情况,令没有去睡觉的熊不碰第 \(x\) 个桶,在第 \(a\) 天去睡觉的熊恰好在第 \(a\) 晚去喝第 \(x\) 个桶里的饮料。
这样子如果第 \(x\) 桶里是酒,就恰好会生成这种情况,所以每种答案对每种情况是一个满射,然而它们数量相同,所以是一一对应的。
所以只要求出这个多项式的系数就行,系数就是组合数模 \(2^{32}\),记一下 \(2\) 的次数,递推一下就行。
时间复杂度为 \(\mathcal O (p \log \mathrm{MOD} + q \cdot p)\),其中 \(\log \mathrm{MOD}\) 为快速幂复杂度,评测链接。
agc024_e
相当于是,从一个空串开始,每次往里面加入一个 \([1, K]\) 之间的字符,加入 \(N\) 次,使得字符串的字典序递增。
先把每个串的末尾加上字符 \(0\)。
可以发现,加入字符(假设我们在字符 \(y\) 前插入字符 \(x\))后字典序递增,当且仅当:
- \(x > y\)。
- \(x = y\),且 \(x > y\) 之后第一个不同的字符。
我们插入的时候,只关心字符串是否相同,不关心插入的位置。
所以假设是第二种情况,我们可以把插入的位置往后挪到那个不同的字符之前。
这样子既不会统计到重复的串,又避免了难考虑的 2 情况,一举两得。
现在只需要考虑 1 情况,也就是每次插入的字符必须插入在一个比它小的字符之前。
我们可以把插入的形式抽象化为一棵树:
根节点为 \(0\),权值也为 \(0\)。
假设第 \(i\) 次在字符 \(y\) 之前插入了字符 \(x\),如果 \(y\) 是在第 \(j\) 次插入的,就令 \(i\) 为 \(j\) 的儿子,权值为 \(x\)。
可以发现这样的树,只需要满足:节点编号为 \(0 \sim N\),节点权值为 \(0 \sim K\),且孩子节点的编号和权值,要分别大于当前节点的编号和权值。
考虑令 \(dp(i, j)\) 表示,一棵 \(i\) 个点的树,节点编号为 \(0 \sim i - 1\),根节点权值为 \(j\),且满足上述条件的方案数。
有转移:\(\displaystyle dp(i, j) = \sum_{k = 1}^{i - 1} \binom{i - 2}{k - 1} dp(i - k, j) \sum_{j < x \le K} dp(k, x)\)。
组合意义是:考虑编号为 \(1\) 的节点,它一定是根节点的孩子,且形成一个子问题,枚举 \(1\) 节点的子树大小,假设为 \(k\),将除了 \(0, 1\) 之外的 \(i - 2\) 个编号分配给除了 \(1\) 之外的 \(k - 1\) 个 \(1\) 的子树中的点,这里贡献一个 \(\displaystyle \binom{i - 2}{k - 1}\);除了 \(1\) 子树外的大小为 \(i - k\),这里贡献一个 \(dp(i - k, j)\);\(1\) 节点的权值为 \((j, K]\) 中的整数,这里贡献一个 \(\displaystyle \sum_{j < x \le K} dp(k, x)\)。
后一个和式用后缀和优化,状态转移的总时间复杂度为 \(\mathcal O (N^2 K)\)。
答案就为 \(dp(N + 1, 0)\)。
时间复杂度为 \(\mathcal O (N^2 K)\),评测链接。
2020-02-10
cf538G
通过坐标变化,把曼哈顿距离转成切比雪夫距离。
也就是说四个方向 RLUD,原本是横纵坐标选取其中一个加减 \(1\),现在变成可以分别确定横纵坐标是加还是减。
所以这就变成了一个一维的问题,好考虑一些。具体地说,只要把 \((x, y)\) 变成 \((x + y, x - y)\) 就行。
接下来考虑一维问题,只要分别解决了两个一维问题,显然就可以拼成答案。
假设操作序列为 \(c\),则 \(c\) 是个 \(\pm 1\) 串。通过 \(x_i \gets (x_i + t_i) / 2\),可以把 \(c\) 转成 \(01\) 串。
则我们考虑 \(c\) 是 \(01\) 串的情况,令 \(s\) 为 \(c\) 的前缀和。
则有 \(s_i \le s_{i + 1} \le s_i + 1\)。
考虑每个时刻,还有 \(x_i = \lfloor t_i / l \rfloor s_l + s_{t_i \bmod l}\)。
令 \(s = s_l\),如果确定了 \(s\),就可以直接判断是否合法了。
具体的说,根据获得的 \(n\) 个时刻的信息,可以确定出 \(s_i\) 中一些位置的值了,然后根据 \(s_i \le s_{i + 1} \le s_i + 1\) 进一步判断。
但是现在不知道 \(s\),如何求出 \(s\) 呢。
我们把所有信息:\(c_i s + s_{p_i} = x_i\) 按照 \(p_i\) 从小到大排序。
(\(c_i = \lfloor t_i / l \rfloor\),\(p_i = t_i \bmod l\))
不过在排序之前,要在这些信息里加上两条:\(0 s + s_0 = 0\) 和 \((-1) s + s_l = 0\)。
然后考虑相邻的两条信息,就可以列出不等式确定 \(s\) 的范围。
最后求得的 \(s\) 是一个区间,任取里面任何一个值都可以。
具体证明我也不太懂,反正 AC 了(
其它实现细节见代码。
时间复杂度为 \(\mathcal O (n \log n + l)\),评测链接。
agc035_d
可以发现 \(A_1\) 和 \(A_N\) 没啥用,不用考虑它们,然后最后加到答案里去就行。
那也就是说,现在有 \(N - 2\) 个数排成一行,你每次可以删掉其中一个,它就会加到左右两边去。
特别的,如果它在最左边,它就会被加到一个变量 \(L\) 上,如果它在最右边,它就会被加到一个变量 \(R\) 上。
最后要让 \(L + R\) 最小。
这时可以考虑倒着做。假设最后一个删掉的元素,是 \(i\)。
那么 \(i\) 左边的数,一部分扔到 \(L\) 里了,一部分扔到 \(i\) 上了,\(i\) 右边的数,一部分扔到 \(R\) 里了,一部分扔到 \(i\) 上了。
然后删除 \(i\) 本身,就有那些扔到 \(i\) 上的数,以及 \(i\) 本身,都会被加到 \(L\) 和 \(R\) 上。
那么我们假设,\(i\) 左边的数删除后,加到 \(i\) 上,总共加了 \(x\)。那么这 \(x\) 最后产生的贡献就是 \(2x\),因为加到了 \(L\) 和 \(R\) 上。
右边同理,只不过换了个方向,也是两倍贡献。
既然倒着考虑了,那就要想到区间 DP。我们观察 \(i\) 左边的区间,这段区间中的数,加到左边会对总答案贡献 \(1\) 倍,但是加到右边会贡献 \(2\) 倍。
于是定义如下状态:\(dp(l, r, cl, cr)\) 表示考虑区间 \([l, r]\) 中的数,把它们删除后,会对总答案贡献 \(cl \cdot L + cr \cdot R\),要使这个贡献最小。
则最终答案为 \(dp(2, N - 1, 1, 1) + A_1 + A_N\)。
有转移:
特别地,如果 \(l > r\),则 DP 值为 \(0\)。
容易发现,DP 状态数的上界是 \(\mathcal O (N^2 2^N)\),因为区间只有 \(\mathcal O (N^2)\) 对,而后面的系数的增长可以看作一个 \(N\) 层的二叉树的形态。
经过一些精细计算,其实 DP 状态数和转移数只有 \(\mathcal O (2^N)\),这里就略去不证了。
时间复杂度为 \(\mathcal O (2^N)\),评测链接。
agc033_e
不失一般性,我们假设 \(S[1] = \texttt{R}\),如果不成立则把两种颜色互换即可,不影响答案。
因为一开始就必须走红弧,所以环上不能出现相邻的蓝弧。也就是说,环上的每一段蓝弧的长度均为 \(1\)。
如果 \(S\) 全部都是 \(\texttt{R}\),则不需要其他限制了,答案就为 \(2F_{N - 1} + F_N\)(\(F\) 为斐波那契数列,\(F_0 = 0, F_1 = 1\))。
否则至少有一个 \(\texttt{B}\),初始的一段 \(\texttt{R}\) 后必然会跟着一个 \(\texttt{B}\),所以那时必须要走到蓝弧旁边。
由此可得,一定不会出现一段连续的红弧,满足长度为偶数。也就是说每段连续的红弧的长度一定是奇数。
如果出现了长度为偶数的红弧,则如果一开始的位置在这段弧上,且到两端的蓝弧的距离的奇偶性和 \(S\) 中第一段 \(\texttt{R}\) 的长度不一样,就一定不可能在 \(\texttt{R}\) 结束时到达蓝弧旁边(注意到因为长度是偶数,才有到两端的蓝弧的距离的奇偶性相同。如果长度为奇数,能保证恰好有一端距离的奇偶性与 \(S\) 中第一段 \(\texttt{R}\) 的长度相同)。
进一步地,假设 \(S\) 中第一段 \(\texttt{R}\) 的长度为 \(l_1\),则每段红弧的长度,不能超过 \((l_1 + [l_1 \bmod 2 = 0])\)(因为恰好有一端是可行的,到那一端的距离不能太大)。
接着,考虑 \(S\) 之后的每一段连续的 \(\texttt{R}\)。
如果这一段 \(\texttt{R}\) 之后没有接着一个 \(\texttt{B}\),也就是说它在 \(S\) 的末尾,那么对它就没有限制。
否则,考虑它的长度,假设为 \(l_i\)。因为这一段 \(\texttt{R}\) 的上一个字符必然也是 \(\texttt{B}\)(不是第一段了),所以一开始时必然是在某一段红弧的端点上。如果 \(l_i\) 为奇数的话,就要走到对面的端点上才行,否则一直在相邻的红弧上反复横跳就行。也就是说,如果 \(l_i\) 为奇数的话,这一段红弧的长度最长不能超过 \(l_i\);如果是偶数的话不产生影响。当然,因为起点是任选的,所以每一段红弧也都具有了这个性质。
总的来说,就是说每一段红弧的长度被限制了,最小是 \(1\),最大不妨令它为 \(k\),且要是奇数。然后要计算形成一个环的方案数。
我们把一段红弧,和它在逆时针方向的第一个蓝弧,算作一段,这样每一段的长度就必须是 \(2 \sim (k + 1)\) 之间的偶数,所以 \(N\) 也必须是偶数。
环上的情况不好考虑,必须要转化成序列。
我们考虑第一个弧所在的那一段,假设那一段的长度为 \(x\),则有 \(x\) 种方法旋转,使得第一个弧仍然在那一段中。
那么也就是说,对于所有的权值是 \(\le k\) 的正偶数,总和为 \(N\) 的序列 \(A\),每一个序列会为答案贡献 \(A_1\) 种方案。
也就是枚举 \(A_1\),然后计算总和为 \(N - A_1\) 的序列的数量,乘以 \(A_1\) 后贡献给答案。
总和为 \(i\) 的序列的个数很好算,只要枚举最后一个元素是多少就行了,有转移:\(\displaystyle f(i) = \sum_{j = 2}^{k} [j \bmod 2 = 0] f(i - j)\)。
用前缀和优化一下就完事了。
时间复杂度为 \(\mathcal O (N + M)\),评测链接。
2020-02-11
cf634F
如果固定上下边界,那么中间的点,按照纵坐标排序,就可以统计答案了。所以这样子是 \(\mathcal O (r^2 n)\) 的。
那我们固定上边界,往下推下边界呢?那就是变成每次插入一个点,会影响它周围的 \(k\) 个点对答案的贡献。
但是动态插入,比较不好维护。那我们就从下往上推下边界,现在就变成删除,可以用链表快速定位和找周围的 \(k\) 个点。
时间复杂度为 \(\mathcal O (n \log n + r^2 + r n k)\),评测链接。
2020-02-12
cf666E
因为不会 SAM,所以用 SA。
我们考虑 Height 数组的 Kruskal 重构树,其实是和后缀树等价的。
那一次询问就是查询一棵子树中,出现次数最多的颜色,以及它出现的次数。
线段树合并即可(好像是我第一次写线段树合并)。
时间复杂度为 \(\mathcal O ((l + q) \log m)\),其中 \(\displaystyle l = |s| + \sum |t_i|\),评测链接。
cf611H
可以发现只要是无序对 \((a_i, b_i)\) 相同的边,都可以只看做一类,这样就只有最多 \(6 (6 + 1) / 2 = 21\) 类边。
同时位数相同的点,也可以看作一类,这样只有最多 \(6\) 类点。
令 \(m = \lfloor \log_{10} n \rfloor + 1\),点的类数就为 \(m\),边的类数就为 \(m (m + 1) / 2\)。
可以发现不同种类的点,不管怎么样也还是要连接起来的。
那么先特判一下 \(m = 1\) 的情况,然后可以证明一个结论:存在一种方案,满足:
- 每一类点都选出一个“关键点”,例如第 \(i\) 类点的关键点编号可以为 \({10}^{i - 1}\)。
- 只考虑这 \(m\) 个关键点,它们形成的导出子图,是一棵树,也就是一个 \(m\) 个点 \(m - 1\) 条边的树连接了所有“关键点”。
- 其它所有点只与“关键点”连接,也就是不存在“非关键点”之间的连边。
详细证明这里从略。
那么,我们考虑枚举连接所有“关键点”的树形态,比如使用 Prüfer 序列枚举,这部分的时间复杂度为 \(\mathcal O(m^{m - 2})\)。
枚举完成后,对应种类的边就用掉了对应条,这里记得先扣掉。
然后考虑每一条边 \((u, v)\),可以是 \(u\) 类“非关键点”连到 \(v\) 类“关键点”上,也可以是 \(v\) 类“非关键点”连到 \(u\) 类“关键点”上。
总之,一条边 \((u, v)\) 将会把 \(u\) 类或者 \(v\) 类的“非关键点”的剩余个数减去 \(1\)。
这样一来就可以转化为一个带权(重数)二分图完美匹配的模型。
具体地说,左侧有 \(m (m + 1) / 2\) 个点,表示每一类边,右侧有 \(m\) 个点,表示每一类点。
左侧的每个点,带的权值(重数)为剩余的对应类型的边的数量。
右侧的每个点,带的权值(重数)为剩余的对应类型的点的数量。
不难发现这两个数量之和相等。左侧的每个点,假设它对应的边的类型为 \((u, v)\),它向右侧的 \(u, v\) 类点对应的点分别连边。
使用网络流可以解决带重数的二分图匹配问题,这里写个 Dinic 水过去。
Dinic 跑完之后也可以直接构造方案了。
时间复杂度为 \(\mathcal O (m^{m + 4})\),评测链接。
2020-02-13
cf613E
对于 \(|w| \le 2\) 的情况,我们进行特判,这是为了之后写起来分类讨论可以简洁一些。
观察一下最终的行走方式可能会变成啥样:

很多情况下,会变成这个样子。
注意到可以分成三段,左边一个 U 形,中间一个只会向右走的形状,右边又一个 U 形。
啊,为啥说中间是只会向右走?因为我们是这么钦点的,当然也可能是从右边出发往左走,这时只要把 \(w\) 反转,再求一次就行。
我们可以处理出,从一个地方分段,会不会产生向左的,长度为某个值的 U 形。
这可以通过预处理 LCP 做到。
同理可以处理出,从一个地方分段,会不会产生向右的,长度为某个值的 U 形。
处理上述两个数组,它们就能够作为第一部分和第三部分。
我们把第二部分接在第一部分后,记 \(f(i, j, k)\) 表示,当前第二部分走到了 \((i, j)\),并且匹配了 \(w\) 的前 \(k\) 个字符,并且不是从同一列走来的方案数。
类似地,记 \(g(i, j, k)\) 为必须从同一列走来的方案数。则 \(f, g\) 之间可以互相转移,这部分可以 \(\mathcal O (n |w|)\) 处理。
然后考虑在 DP 到 \((i, j, k)\) 时,接上第三部分即可,可以直接判断接不接得上。
当然还有一些其他情况没有讨论的,比如三个部分中的某一部分并不存在,甚至是两个部分不存在之类的,仔细讨论一下即可。
注意要不重不漏,特别注意 \(w\) 反转后不要统计重复了。
时间复杂度为 \(\mathcal O (n |w|)\),评测链接。
cf566E
如果两个集合的交为 \(2\),则交出来的这两个点,之间一定有连边。
这样可以确定树中所有非叶子节点之间的连边情况。
先特判非叶子节点数为 \(0, 1, 2\) 的情况。
为 \(0\) 的话就是 \(n = 2\);为 \(1\) 的话就是菊花,每个集合大小都是 \(n\);为 \(2\) 的话就是有恰好两个集合大小是 \(n\)。
现在非叶子节点数至少是 \(3\)。那么我们需要确定每个叶子挂在了哪个非叶子上。
注意到我们在给非叶子节点连边的时候,就可以处理出每个非叶子节点,与其相连的非叶子节点的集合,也就是距离 \(\le 1\) 的集合。
那么我们依次考虑每个叶子,它对应的集合就是所有集合中,包含这个叶子的,大小最小的那个。
在这个集合中,去掉所有叶子节点,就得到了与它相连的非叶子节点的邻接非叶子节点集合。
再枚举每个非叶子节点,就可以判断具体是和哪一个非叶子节点相连的了。
时间复杂度为 \(\displaystyle \mathcal O \!\left( \frac{n^3}{w} \right)\),其中 \(w\) 为字长,评测链接。
cf573E
考虑一个贪心策略:一开始选空集,然后每次选一个不在集合中的数加入集合,具体选哪个数呢?选择让新的答案最大的数即可。
然后集合大小从 \(0\) 逐渐增大到了 \(n\),得到了 \(n + 1\) 个答案,我们选取其中最大的一个输出。
我们发现这样做成功 TLE 了(悲),但是并没有 WA,说明贪心是对的(确信)。
具体证明请下载 徐翊轩的题解 查看。
那么我们只需要快速维护这个贪心,具体地说,每个位置有一个权值 \(b_i\) 和一个固定的值 \(a_i\),需要支持四种操作:
- 前缀 \(b_i\) 加相同值。
- 后缀 \(b_i\) 加 \(a_i\)。
- 查询 \(b_i\) 的全局最大值。
- 删除一个位置。
一般线段树没法做,我们考虑分块。(其实这是一种经典分块类型)
每 \(\sqrt{n}\) 个元素分一块,那对于每一块就要实现:
- 整体加。
- 整体加 \(a_i\)。
- 查询整体最大值。
- 重构。
可以发现大概是类似斜率优化那套式子,维护上凸壳即可。
注意到 \(a_i\) 始终不变,而要求的斜率不断递减,可以用单调队列维护,重构的时候也不用重新排序了。
本题还有 \(\mathcal O (n \log n)\) 的做法,在题解中同样可以看到。不过因为要手写平衡树,我比较懒就不写了。
时间复杂度为 \(\mathcal O (n \sqrt{n})\),评测链接。
2020-02-18
cf627F
设初始时 \(0\) 在 \(s\),目标时在 \(t\)。
注意到操作的本质是 \(0\) 的移动,同时操作具有可逆性。
因此,我们先不考虑次数最少的要求,先让 \(0\) 从 \(s\) 以最短距离移动到 \(t\)。
如果此时已经满足目标状态了,说明不需要加入新的边,此时 \(0\) 经过的距离即为最少步数。
否则,接下来我们只能加入一条新的边,然后让 \(0\) 从 \(t\) 出发,走到包含这条新边的环上距离 \(t\) 最近的点 \(p\),绕若干次完整的圈之后,回到 \(t\)。
观察这样操作对权值的变化可以得出,\(t\) 到 \(p\) 的路径上的所有点的权值都不会改变,同时每绕圈一次,环上除了 \(p\) 之外的点上的权值变化形成一个循环,而绕若干圈则为一个轮换。
因此,权值要改变的点加上 \(p\) 应该在树上形成一条路径。
由此我们能够确定连边 \((u,v)\),可以 \(t\) 为根,找到所有权值需要改变的点,\(p\) 即为这些点中深度最小的点的父节点,而路径 \((u,v)\) 则由 \(p\) 和这些点构成。
如果深度最小的点的父节点不唯一,或者 \(p\) 和这些点无法构成一条路径,或者这些点的权值不是目标权值的一个轮换,则说明无解。
最后来考虑最小化操作次数。
对于一条加边 \((u,v)\),绕圈的方向有两种 \(u \to v\) 和 \(v \to u\),分别计算取 \(\min\) 即可。
假设从 \(u \to v\),由这个轮换对循环的次数 \(c\) 可以得到最小次数为 \(2\cdot \operatorname{dist}(t, p) + c \cdot (\operatorname{dist}(u, v) + 1)\)。
但注意这个最小次数是在先将 \(0\) 从 \(s\) 移到 \(t\) 的前提下,因此如果有重复的路径需要减掉。
准确地说,如果是 \(u \to v\),那就是将 \(0\) 直接从 \(s\) 经过树边移动到 \(u\),然后经过新加的边移动到 \(v\),然后在这个环上再绕 \((c - 1)\) 圈回到 \(v\),最后经过树边移动到 \(t\)。此时的答案也就是 \(\operatorname{dist}(s, u) + (c - 1) \cdot (\operatorname{dist}(u, v) + 1) + \operatorname{dist}(v, t) + 1\)。
如果是 \(v \to u\),只要把 \(u, v\) 互换,并重新计算循环的次数 \(c\) 即可。
时间复杂度为 \(\mathcal O (n)\),评测链接。
2020-02-19
arc093_f
淘汰赛的比赛结构是一个完全二叉树,假设玩家 \(1\) 被安排在了某个位置,则他要最终获得胜利的话,需要打败 \(N\) 个对手。
这 \(N\) 个对手分别来自大小为 \(2^0, 2^1, 2^2, \ldots , 2^{N - 1}\) 的子树中。
也就是说,它们是那些对应的子树中的最小值。
要让 \(1\) 取得胜利,这些值中不能有那 \(M\) 个 \(A_i\) 之一。
这相当于,把除了 \(1\) 以外的 \(2^N - 1\) 个数染上 \(N\) 种颜色,第 \(i\) 种颜色恰好要染 \(2^{i - 1}\) 个数。
而且对于每种颜色,最小的,染上这种颜色的数,不能是任何一个 \(A_i\)。
然后我们考虑容斥原理,假设一个集合中的 \(A_i\) 都必须是某个颜色的最小值。
可以发现让 \(A_i\) 从大到小 DP 会比较合适。记一个状态表示比当前值大的 \(A_i\) 被强制选取了哪些颜色的最小值,也就是说哪些颜色已经被用掉了。
转移的时候,该 \(A_i\) 可以不强制选,直接转移;或者强制选成某个还未被选择的颜色 \(k\) 的最小值,DP 值乘上 \(\displaystyle \binom{s - 1}{2^{k - 1} - 1}\),其中 \(s\) 表示后面还没有被选中的数的个数,\(s\) 可以直接由当前 \(A_i\) 和选取的颜色状态计算得出。
最后答案就是容斥得到的染色方案数,乘以 \(\displaystyle 2^N \prod_{i = 1}^N (2^{i - 1})!\),这是因为每个子树内可以任意排,然后 \(1\) 每次可以从左子树或右子树上来。
时间复杂度为 \(\mathcal O (M N 2^N)\),评测链接。
2020-02-20
cf506E
不考虑题目中的“在原串中插入”,我们直接统计最终的长度为 \(N = |s| + n\) 的回文串的个数。
接下来的问题是:给定一个回文串,如何判断 \(s\) 是否作为一个子序列出现。
当然可以直接子序列自动机,但是这样子的性质不够好。考虑从 \(s\) 的两侧进行匹配。
假设当前回文串为 \(t\),我们使用 \(t\) 两侧的字符对 \(s\) 两侧的字符进行匹配:
假设 \(t\) 两端的字符为 \(c\),如果 \(s\) 左端的字符也为 \(c\),就删去这个字符,右边同理。
以 \(s = \mathtt{abaac}, t = \mathtt{{\color{red}b}{\color{magenta}a}{\color{blue}c}{\color{Tan}b}{\color{ForestGreen}a}{\color{Tan}b}{\color{blue}c}{\color{magenta}a}{\color{red}b}}\) 为例:
- 用 \(\mathtt{{\color{red}b}}\) 去匹配 \(s\) 的两端,\(s\) 变为 \(\mathtt{abaac}\)。
- 用 \(\mathtt{{\color{magenta}a}}\) 去匹配 \(s\) 的两端,\(s\) 变为 \(\mathtt{{\color{magenta}a}baac}\)。
- 用 \(\mathtt{{\color{blue}c}}\) 去匹配 \(s\) 的两端,\(s\) 变为 \(\mathtt{{\color{magenta}a}baa{\color{blue}c}}\)。
- 用 \(\mathtt{{\color{Tan}b}}\) 去匹配 \(s\) 的两端,\(s\) 变为 \(\mathtt{{\color{magenta}a}{\color{Tan}b}aa{\color{blue}c}}\)。
- 用 \(\mathtt{{\color{ForestGreen}a}}\) 去匹配 \(s\) 的两端,\(s\) 变为 \(\mathtt{{\color{magenta}a}{\color{Tan}b}{\color{ForestGreen}a}a{\color{blue}c}}\)。
注意,这里只能匹配其中一个字符,因为 \(\boldsymbol{t}\) 中只剩下一个 \(\mathtt{{\color{ForestGreen}a}}\) 了!
如果 \(s\) 少一个 \(\mathtt{a}\) 或者 \(t\) 多一个 \(\mathtt{{\color{ForestGreen}a}}\),就能全部匹配。
如果按照这种方式全部匹配完了,就是合法的串。
由此我们可以构造一个 DP:\(dp(x, i, j)\) 表示确定了 \(t\) 的左右两端各 \(x\) 个字符后,恰好匹配到 \(s\) 中的子串 \(s[i : j]\) 的 \(t\) 的方案数。
并且一个特殊的状态 \(dp(x, \mathrm{done})\) 表示匹配完了。
则答案就为 \(\displaystyle dp \!\left( \left\lceil \frac{N}{2} \right\rceil\!, \mathrm{done} \right)\)。
对应的转移图如下:
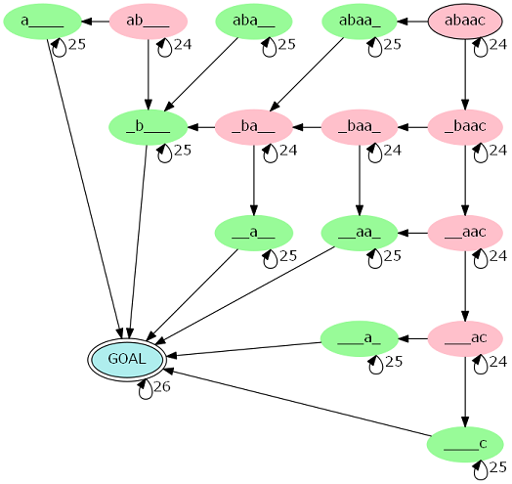
但是因为 \(N\) 太大,没法直接这样做,直接做的复杂度是 \(\mathcal O ({|s|}^2 N)\) 的。
观察到这个转移图,显然就是用来矩阵快速幂的,但是还是不行,复杂度是 \(\mathcal O ({|s|}^6 \log N)\) 的。
所以还是观察一下性质,比如我们可以发现,红色点就代表 \(s\) 的两端不同的情况,绿色点表示相同的情况。
那么要到达终点,如果经过了 \(n_1\) 个红色点,就必须要经过 \(\displaystyle \left\lceil \frac{|s| - n_1}{2} \right\rceil\) 个绿色点。
然后发现终点前的点一定是绿色点,所以最多经过 \(|s| - 1\) 个红色点,也就是说经过的红色点的数量在 \(0\) 到 \(|s| - 1\) 内。
我们单独把一条从起点到终点的链拿出来,可以发现,经过的红点和绿点的顺序实际上没有影响,也就是说把红点提前答案不变:

这个性质十分重要,因为本质不同的链的个数只有 \(\mathcal O (|s|)\) 个,所以只要求出每种链的个数就行了,同样可以使用类似的 DP 得到。
这样的话,考虑在每一条链上做矩阵快速幂,得到的答案乘以链的条数再相加就是总答案,复杂度是 \(\mathcal O ({|s|}^4 \log N)\) 的。
我们可以更进一步优化,考虑这样的自动机(字符串长度为 \(|s| = 5\) 时,也就是和刚才举的例子相同):
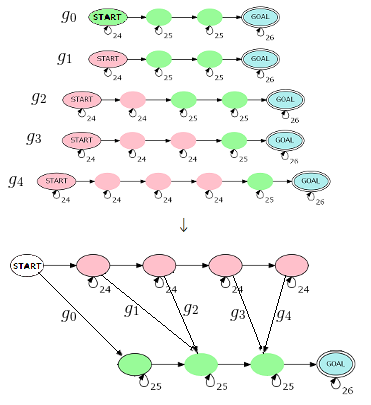
其中 \(g_0 \sim g_{|s| - 1}\) 分别表示经过的红点个数分别为对应值的链的个数。
可以发现恰好满足每一条本质不同的链都能够被表示出,而且不重复不遗漏。
在这个自动机上做矩阵快速幂就行了,因为加了一个空的起点,所以要多走一步。
但是这样直接求的话,对于 \(N\) 是奇数的情况会多算,就是前文提到的那种情况(最中心的字符只能匹配一个)。
我们这样考虑,先求出在 \(\displaystyle \left\lfloor \frac{N}{2} \right\rfloor\) 步内就能到达终点的方案数,乘以 \(26\)(还能再走一步)。
然后再加上在 \(\displaystyle \left\lfloor \frac{N}{2} \right\rfloor\) 步时恰好到达一开始的自动机中的 \(s\) 被删到长度为 \(1\) 时的节点的方案数。
计算第二种情况时,也要重新计算一下 \(g_0 \sim g_{|s| - 1}\),最终就能求得总答案了。
时间复杂度为 \(\mathcal O ({|s|}^3 \log N)\),评测链接。
arc096_e
考虑容斥,枚举有 \(a\) 个只出现了一次,\(b\) 个一次都没出现。
则给答案贡献 \(\displaystyle {(-1)}^{a + b} \binom{n}{a} \binom{n - a}{b} 2^{2^{n - a - b}} \sum_{x = 0}^{a} {a \brace x} {(2^{n - a - b})}^x\)。
如果令 \(c = a + b\),变换为 \(\displaystyle {(-1)}^c \binom{n}{c} 2^{2^{n - c}} \sum_{x = 0}^{c} {(2^{n - c})}^x \sum_{a = x}^{c} {a \brace x} \binom{c}{a}\)。
考虑这个恒等式:\(\displaystyle \sum_{i = x}^{n} {i \brace x} \binom{n}{i} = {n + 1 \brace x + 1}\)。
所以答案为 \(\displaystyle \sum_{c = 0}^{n} {(-1)}^c \binom{n}{c} 2^{2^{n - c}} \sum_{x = 0}^{c} {(2^{n - c})}^x {c + 1 \brace x + 1}\)。
时间复杂度为 \(\mathcal O (N^2 + N \log M)\),评测链接。
2020-02-21
cf575E
可以证明如下结论:
在平面直角坐标系中,给定若干个不全都共线的点。
要作一个半径尽量大的圆,使得该圆包含所有给定点,并经过至少三个给定点。
构造给定点构成的凸包,并要求凸包上不存在共线的三个顶点。由于这些点不全都共线,所以一定存在这样的凸包。
则有结论:要求的圆一定经过凸包上三个相邻顶点。
具体证明请下载 任清宇的题解 查看。
所以只要求出给出的点集的凸包后,枚举凸包上相邻三点计算并更新答案即可。
具体地说,由于每个人能够到达的点的凸包是一个点,或一个 \(3 \sim 6\) 边形,只要求出每个人对应的凸包的顶点,这可以通过简单的讨论求出,再合并求一次大凸包即可。
时间复杂度为 \(\mathcal O (n \log n)\),评测链接。
cf607E
为了方便考虑,把坐标系平移到以 \((p, q)\) 为原点处。
那么以原点为圆心作圆,只要找到圆内有 \(m' < m\) 个交点的最大半径即可。
那么答案就等于圆内交点到原点的距离之和,加上 \(m - m'\) 倍的半径。
二分答案后考虑如何 check 是否有 \(< m\) 个交点。
把每个与圆有交的直线拿出来,就变成圆上的一条弦,对应了圆上极角序的一个区间。
就变成了对相交但不包含的区间对计数的问题,是二维偏序问题。
这部分时间复杂度为 \(\mathcal O (n \log n (\log v - \log \varepsilon))\)。
确定了对应半径后,再使用类似方法在 \(\mathcal O (n \log n + m)\) 的时间内统计交点到原点的距离即可。
时间复杂度为 \(\mathcal O (n \log n (\log v - \log \varepsilon) + m)\),评测链接。
2020-02-22
arc092_f
对于一条边 \(u \to v\),将它反向后变成 \(v \to u\),会对原图的强连通分量个数造成影响,当且仅当:
- 忽略这条边后,\(u\) 能直接或间接到达 \(v\)。
- 忽略这条边后,\(v\) 能直接或间接到达 \(u\)。
这两个条件仅恰好满足一个。证明不难,请自行脑补。
其中,忽略 \(u \to v\) 后,询问 \(v\) 是否能够到达 \(u\),和不忽略其实也没啥区别,所以这部分可以直接做,\(\mathcal O (NM)\) 的复杂度就可以接受了,当然你也可以用 bitset 做 \(\mathcal O (M + NM / w)\)。
然后考虑忽略 \(u \to v\) 后,询问 \(u\) 是否能够到达 \(v\),也就是只要存在第一条边不走 \(u \to v\) 的简单路径就行。
我们考虑对于所有的起点相同,也就是 \(u\) 相同的 \(u \to v\) 计算这个东西,那么只要一次的时间复杂度为 \(\mathcal O (M)\) 就可以接受了。
首先把 \(u\) 的出边排成一排,假设终点分别为 \(v_1, v_2, \ldots , v_k\)。
那么先按照正序,也就是 \(v_1, v_2, \ldots , v_k\) 的顺序进行 DFS,并记录每个点是从哪个点到达的(就是从哪个 \(v_i\) 出发),记做 \(p(v_i)\)。
然后按照逆序,也就是 \(v_k, v_{k - 1}, \ldots , v_1\) 的顺序进行 DFS,并记录每个点是从哪个点到达的,记做 \(q(v_i)\)。
如果一个 \(v_i\) 可以从其它 \(v_j\)(\(j \ne i\))出发到达它,当且仅当 \(p(v_i) \ne q(v_i)\),只要判断这个条件即可。
时间复杂度为 \(\mathcal O (NM)\),评测链接。
2020-02-23
agc023_f
第一步,必须把根节点删掉。
然后可以发现,如果删掉一个节点之后,它的孩子中有 \(0\),那就可以立刻把孩子也删掉,这样答案不会变得更劣。
那我们把 \(0\) 和它的父亲并成一个连通块,表示这个连通块可以一次性取完,最后整棵树就变成了一些不相交连通块。
然后会发现,如果此时我们把每个连通块看成一个节点,还是一棵树的结构,但是这时每个连通块内就有若干个 \(0\) 和 \(1\) 混合了。
现在仅考虑新树的两个节点 \(u, v\),忽略其它的影响:
假设 \(x\) 中 \(0, 1\) 的个数分别为 \(x_0, x_1\),则如果 \(u\) 排在 \(v\) 前面,就会增加 \(u_1 v_0\) 对逆序对,反之增加 \(v_1 u_0\) 对。
如果 \(u_1 v_0 < v_1 u_0\),则 \(u\) 排在 \(v\) 前面肯定更优。
变换一下式子,变成 \(\displaystyle \frac{u_1}{u_0} < \frac{v_1}{v_0}\),也就是连通块中 \(1\) 与 \(0\) 个数的比值。
考虑当前这个比值最小的连通块,假设为 \(a\),则可以发现当 \(a\) 的父亲被取到的时候,下一步一定会把 \(a\) 取了。
这是因为无论连通块怎么合并,这个比值都不会变得比原来更小,也就不会小于 \(a\) 的比值。
所以,拿一个支持插入删除,取出最小值的数据结构(比如 set),就可以维护了。
具体地说就是每次取出这个比值最小的连通块,把它的它的父亲合并。
时间复杂度为 \(\mathcal O (n \log n)\),评测链接。
2020-02-25
agc038_f
把 \(P\) 分解成不相交循环的乘积后,考虑其中一个循环 \((a_1, a_2, \ldots , a_k)\)。
不失一般性,可以把这个循环看作 \((1, 2, \ldots , k)\)。
那么对于 \(A_1\),有两种情况:\(A_1 = 1\) 或 \(A_1 = P_1 = 2\)。
如果 \(A_1 = 1\),则考虑 \(A_k\) 有两种情况:\(A_k = k\) 或 \(A_k = P_k = 1\),但是因为 \(A_1 = 1\),所以只能有 \(A_k = k\)。
以此类推,可以得到:对于这个循环中的所有元素 \(i\),均有 \(A_i = i\)。
如果 \(A_1 = 2\),则考虑 \(A_2\) 有两种情况:\(A_2 = 2\) 或 \(A_2 = P_2 = 3\),但是因为 \(A_1 = 2\),所以只能有 \(A_2 = 3\)。
以此类推,可以得到:对于这个循环中的所有元素 \(i\),均有 \(A_i = P_i\)。
换句话说,对于每个循环,要么这个循环被完全保留,要么这个循环被完全拆解成一个个自环。
上述结论对 \(Q\) 和 \(B\) 当然也适用。
我们称选择一个循环,指这个循环被完全保留,称不选一个循环,指这个循环被拆解成了一个个自环。
接着,考虑一个 \(P\) 中的循环 \(a\) 和一个 \(Q\) 中的循环 \(b\),假设它们共有一个元素 \(i\)。分若干类讨论:
- \(P_i = Q_i = i\):无论如何,这个位置上均有 \(A_i = B_i\)。
- \(P_i = i, Q_i \ne i\):如果选择了 \(b\),则这个位置上有 \(A_i \ne B_i\),否则不选 \(b\),则这个位置上有 \(A_i = B_i\)。
- \(P_i \ne i, Q_i = i\):如果选择了 \(a\),则这个位置上有 \(A_i \ne B_i\),否则不选 \(a\),则这个位置上有 \(A_i = B_i\)。
- \(P_i \ne i, Q_i \ne i, P_i \ne Q_i\):如果不选 \(a\) 且不选 \(b\),则这个位置上有 \(A_i = B_i\),否则这个位置上有 \(A_i \ne B_i\)。
- \(P_i \ne i, Q_i \ne i, P_i = Q_i\):如果 \(a, b\) 同时选择或同时不选,则这个位置上有 \(A_i = B_i\),否则这个位置上有 \(A_i \ne B_i\)。
最终需要最大化 \(A_i \ne B_i\) 的下标 \(i\) 的数量,也就是最小化 \(A_i = B_i\) 的下标 \(i\) 的数量。
如果在上述 \(5\) 种情况中,一旦发生了 \(A_i = B_i\),就赋有 \(1\) 的代价,那么就是要最小化总代价。
可以发现类似于一个文理分科模型,可以建立一个网络流模型,求最小割得到答案。
但是因为有些条件不符合,没法直接套用。
不过,如果把 \(Q\) 中的循环割掉与源点和汇点之间的边的意义交换,就可以套用了。
而且可以发现,这样建出来的图是一个二分图,因为 \(P\) 中的循环只和源点连边,\(Q\) 中的循环只和汇点连边,\(P, Q\) 之间也只会互相连边。(如果 \(P\) 中的循环对应的节点,割掉与源点相连的边的意义是不选它,而 \(Q\) 中的循环对应的节点的意义恰好相反的话)
所以最终是在单位容量的二分图上求最小割,使用 Dinic 算法可以做到 \(\mathcal O (|E| \sqrt{|V|})\) 的复杂度。
时间复杂度为 \(\mathcal O (N \sqrt{N})\),评测链接。
agc023_d
如果 \(X_1 < S < X_N\),考虑第 \(1\) 栋楼和第 \(N\) 栋楼。
如果 \(P_1 \ge P_N\),即第 \(1\) 栋楼中的人数大于等于第 \(N\) 栋楼中的人数,则班车一定会先去第 \(1\) 栋楼。证明:
- 如果 \(N = 2\),显然成立。
- 如果 \(N \ge 3\) 且 \(X_{N - 1} < S\),显然除了第 \(N\) 栋楼的员工,都希望前往负方向,所以一定会前往负方向。
- 如果 \(N \ge 3\) 且 \(S < X_{N - 1}\),如果在到达第 \(1\) 栋楼之前没有到达第 \(N - 1\) 栋楼,则结论成立,否则转化为前两种情况。
所以说不管怎么样都会先前往第 \(1\) 栋楼,然后就可以一路向右径直跑到第 \(N\) 栋楼。
这就意味着,第 \(N\) 栋楼中内的员工的回家时间,一定等于第 \(1\) 栋楼的回家时间,加上 \(X_N - X_1\)。
也就是说,第 \(N\) 栋楼中的员工,其实是和第 \(1\) 栋楼中的员工站在同一条线上的。第 \(1\) 栋楼的员工想投什么票,他们也一定会跟着投。所以说这第 \(N\) 栋楼的员工其实和第 \(1\) 栋楼的员工没什么区别,暂时(在第 \(1\) 栋楼的员工回家之前)让他们搬家到第 \(1\) 栋楼也对运行路径没有影响。
所以说,如果让 \(P_1 \gets P_1 + P_N\),然后删去第 \(N\) 栋楼,计算这种情况下的到达第 \(1\) 栋楼的时间,加上 \(X_N - X_1\) 就是答案。
如果 \(P_1 < P_N\),那么以上结论的方向反过来即可。
这样递归下去,直到不满足 \(X_1 < S < X_N\) 为止,那样的话就可以直接计算答案了。
时间复杂度 \(\mathcal O (N)\),评测链接。
2020-02-26
agc036_d
考虑差分约束模型,图中不存在负环等价于存在一组合法的差分约束的解。
考虑每个节点作为一个变量,第 \(i\) 个节点对应的变量为 \(x_i\)。
因为初始的边不能删去,所以一定有 \(x_i \ge x_{i + 1}\)。
考虑令 \(q_i = x_i - x_{i + 1}\),那么就会有 \(q_i \ge 0\)。
假设保留了一条边权为 \(-1\) 的 \(i \to j\) 的边,也就是说 \(i < j\) 的话:
就会有 \(x_i - 1 \ge x_j\),即 \(x_i - x_j \ge 1\),也就是说 \(q_i + q_{i + 1} + \cdots + q_{j - 1} \ge 1\)。
假设保留了一条边权为 \(1\) 的 \(i \to j\) 的边,也就是说 \(i > j\) 的话:
就会有 \(x_i + 1 \ge x_j\),即 \(x_j - x_i \le 1\),也就是说 \(q_j + q_{j + 1} + \cdots + q_{i - 1} \le 1\)。
反过来想,如果确定了所有的 \(q_i\),那么每一条边就应该尽可能地保留下来,这样代价最小。
对于边权为 \(-1\) 的边,是区间和 \(\ge 1\) 才能保留,也就是说如果区间和 \(= 0\) 就必须删除。
对于边权为 \(1\) 的边,是区间和 \(\le 1\) 才能保留,也就是说如果区间和 \(\ge 2\) 就必须删除。
也就是说,对于一种 \(q\) 的取值方案,\(q_i = 0\) 的每个连续段,都对应着一系列的边权为 \(-1\) 的边的删除。
而区间和 \(\ge 2\) 的区间也对应着边权为 \(1\) 的边的删除。
显然可以发现,如果出现了 \(q_i \ge 2\),不如把它变成 \(1\),这样一定会变得更优(边 \(i \to (i + 1)\) 不用被删除了)。
所以只需要考虑 \(q\) 的取值为 \(\{0, 1\}\) 的情况。
然后可以发现,每个 \(0\) 的连续段就对应着一部分区间的删除,所以考虑如下 DP:
记 \(dp(i, j)\) 表示考虑到了 \(q_i\),最后一个 \(1\) 取在了 \(q_i\),倒数第二个 \(1\) 取在了 \(q_j\) 处的情况下,可以确定的代价的最小值。
\(dp(i, j)\) 可以从 \(dp(j, k)\) 转移而来,利用二维前缀和可以快速求出转移系数。
时间复杂度为 \(\mathcal O (N^3)\),评测链接。
2020-02-27
agc026_e
令 \(a_i\) 表示第 \(i\) 个 \(\mathtt{a}\) 的位置,\(b_i\) 表示第 \(i\) 个 \(\mathtt{b}\) 的位置。
考虑如何比较两个字符串的字典序,可以发现当某个前缀相同时应该比较后缀,所以考虑从后往前 DP:
令 \(dp(i)\) 表示只考虑所有的 \(a_{i \sim N}\) 和 \(b_{i \sim N}\),也就是第 \(i\) 对以及之后的 \(\mathtt{a}, \mathtt{b}\) 的情况下的字典序最大的串。
注意不是第 \(i\) 对 \(\mathtt{a}, \mathtt{b}\) 以及它们之后的所有字符都一定选择,而是一对一对的选择的。
那么答案就为 \(dp(1)\)。而 \(dp(i)\) 可以从两个方向转移,也就是 \(a_i\) 和 \(b_i\) 保留或者删掉。
如果删掉,就直接从 \(dp(i + 1)\) 转移而来。
否则考虑如果保留第 \(i\) 对 \(\mathtt{a}, \mathtt{b}\) 的话会怎么样,根据先后顺序分成两类讨论:
- \(a_i < b_i\):也就是形如 \(\cdots \mathtt{{\color{red}a}{\color{blue}a}{\color{green}b}{\color{blue}a}{\color{blue}a}{\color{green}b}{\color{red}b}} \cdots\) 的情况。
红色的字符就是第 \(i\) 对 \(\mathtt{a}, \mathtt{b}\),绿色的字符表示第 \(i\) 对之前的字符,蓝色的字符表示第 \(i\) 对之后的字符。
注意绿色的字符只可能是 \(\mathtt{b}\),而蓝色的字符只可能是 \(\mathtt{a}\)。因为绿色的字符不会被保留,之后忽略它们。
既然已经确定了必须选取 \(a_i, b_i\),因为要让字典序尽量大,所以 \(a_i\) 到 \(b_i\) 之间所有的 \(\mathtt{a}\) 都应该被删掉。
也就是说,\(dp(i)\) 就应该等于 \(\mathtt{ab} + dp(k)\),其中 \(k\) 为完全在 \(b_i\) 之后的第一对 \(a_k, b_k\) 的编号。 - \(a_i > b_i\):也就是形如 \(\cdots \mathtt{{\color{red}b}{\color{blue}b}{\color{green}a}{\color{blue}b}{\color{blue}b}{\color{green}a}{\color{red}a}} \cdots\) 的情况。
红色的字符就是第 \(i\) 对 \(\mathtt{a}, \mathtt{b}\),绿色的字符表示第 \(i\) 对之前的字符,蓝色的字符表示第 \(i\) 对之后的字符。
注意绿色的字符只可能是 \(\mathtt{a}\),而蓝色的字符只可能是 \(\mathtt{b}\)。因为绿色的字符不会被保留,之后忽略它们。
既然已经确定了必须选取 \(a_i, b_i\),因为要让字典序尽量大,所以 \(a_i\) 到 \(b_i\) 之间所有的 \(\mathtt{b}\) 都应该被保留。
而确定要保留这些 \(\mathtt{b}\),又会导致往后包含了更多的 \(\mathtt{b}\),同理被包含的 \(\mathtt{b}\) 也应该被保留,连锁反应会一直进行下去,直到某一次不包含了更多的 \(\mathtt{b}\) 为止。举个例子:
考虑 \(\mathtt{{\color{blue}b}b{\color{blue}a}babbbabaaaabbabaaaabb}\),
选取 \(\mathtt{{\color{red}b}{\color{blue}b}{\color{red}a}b{\color{blue}a}bbbabaaaabbabaaaabb}\),
选取 \(\mathtt{{\color{red}{bba}}{\color{blue}b}{\color{red}a}bbb{\color{blue}a}baaaabbabaaaabb}\),
选取 \(\mathtt{{\color{red}{bbaba}}{\color{blue}{bbb}}{\color{red}a}b{\color{blue}{aaa}}abbabaaaabb}\),
选取 \(\mathtt{{\color{red}{bbababbba}}{\color{blue}b}{\color{red}{aaa}}{\color{blue}a}bbabaaaabb}\),
选取 \(\mathtt{{\color{red}{bbababbbabaaaa}}bbabaaaabb}\)。
在这种情况下,\(dp(i) = \mathtt{bbababbbabaaaa} + dp(k)\),其中 \(k\) 为后面部分的第一对 \(a_k, b_k\) 的编号。
所以只要求出以上两类的结果就行,第 1 类可以预处理,第 2 类的开头的字符串,可以直接扫一遍判断。
时间复杂度为 \(\mathcal O (N^2)\),评测链接。
cf679E
注意到在可能的值域(约为 \({10}^{14}\))内,\(42\) 的次幂并不多,尝试从这个角度考虑。
操作 3 比较棘手,解决的办法是用线段树维护当前值到下一个 \(42\) 的次幂的差值。
做操作时让这个差值做区间减法,在线段树递归的时候,如果差值会变成负数,就需要再递归进子区间进行修改,但是如果这个区间被打上了区间覆盖标记,就直接修改这个标记就行。
执行完后,如果存在差值为 \(0\) 的位置,就再执行一次。
这个做法的复杂度,使用势能函数可以分析得出为 \(\mathcal O (q \log n \log_{42} v)\)。
具体地说,令当前线段树的势能函数等于每个值相同的连续段,比此连续段的值大的,在值域内的 \(42\) 的次幂的个数的总和,乘以 \(\log n\)。
则操作 2 和操作 3 的摊还代价都为 \(\mathcal O (\log n \log_{42} v)\)。
时间复杂度为 \(\mathcal O ((n + q) \log n \log_{42} v)\),其中 \(v\) 为值域,约为 \({10}^9 q\),评测链接。
2020-02-28
agc039_e
令 \(n = 2 N\),枚举第 \(n\) 个点和哪个点连了,假设为 \(k\),即:

就分成了 \(1 \sim (k - 1)\) 和 \((k + 1) \sim (n - 1)\) 两段。
直接考虑如果是区间 \([i, j]\),且这区间中的一点 \(k\) 与区间外的一点连线了,即:
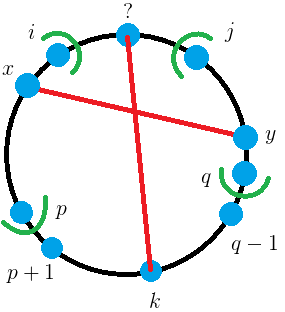
如果 \(i < j\),那么被 \(k\) 分割的左右两边必然要通过至少一条线与 \((? \leftrightarrow k)\) 连接起来
但是又不能交叉,如果交叉就形成环了,所以取最上方的一条线 \((x \leftrightarrow y)\)。
所谓最上方,形式化地说就是 \(x\) 最靠近 \(i\),\(y\) 最靠近 \(j\)。
那么,\(x, y\) 在两边必然就会有各自的“管辖范围”。
(你可以理解成,从 \((? \leftrightarrow k)\) 和 \((x \leftrightarrow y)\) 的交点出发向 \(x\) 或 \(y\) 方向走,能遍历到的区域,它和其它区域不相交)
假设这个范围分别为 \([i, p]\) 和 \([q, j]\)。
那么如果我们枚举 \(i, j, k, x, y, p, q\)(满足 \(i \le x \le p < k < q \le y \le j\)):
就可以转化成三个子问题 \([i, p](x)\) 和 \([p + 1, q - 1](k)\) 和 \([q, j](y)\)。
可以在 \(\mathcal O (n^7)\) 的复杂度内解决此问题,因为常数大约是 \(1 / 7! = 1 / 5040\),所以其实是可以过的。
不过可以继续优化,可以发现 \([i, p]\) 和 \([q, j]\) 是和 \(k\) 独立的,也就是如果 \([i, j]\) 固定,\(k\) 的位置不影响 \(p, q\) 的选择。
那么我们考虑先枚举 \(p, q\),得到 \([i, p] \circ [q, j]\) 这个子问题,再在子问题里枚举 \(x, y\)。
则处理所有 \([i, q] \circ [q, j]\) 就可以做到 \(\mathcal O (n^6)\) 的复杂度(枚举 \(6\) 个变量)。
外层的 \([i, j](k)\) 就可以只枚举 \(p, q\) 进行转移,这部分复杂度为 \(\mathcal O (n^5)\)。
总时间复杂度为 \(\mathcal O (n^6)\),同样带了一个 \(1 / 6! = 1 / 720\) 的常数。
不过可以继续优化,现在复杂度瓶颈是在 \([i, p] \circ [q, j]\) 这里,需要枚举 \(x, y\) 才能转移。
如果只枚举一个 \(y\) 呢?
那就需要求 \([i, p]\) 区间中的,从 \(y > p\) 连进来一条边的方案数,用记号 \([i, p]\{y\}\) 表示。
当然还有本来就要求的 \([q, j](y)\),这个是旧的东西了。
那么考虑计算 \([i, p]\{y\}\),这时就可以枚举具体是和哪个 \(i \le x \le p\) 连边,然后直接加上 \([i, p](x)\) 即可。
所以处理所有 \([i, p]\{y\}\) 的复杂度为 \(\mathcal O (n^4)\),而处理所有 \([i, p] \circ [q, j]\) 的复杂度降为 \(\mathcal O (n^5)\)。
总时间复杂度为 \(\mathcal O (n^5)\),带了一个 \(1 / 5! = 1 / 120\) 的常数,评测链接。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号