Codeforces 1338E: JYPnation
题目传送门:CF1338E。
题意简述
给定一张 \(n\) 个点的竞赛图,特别地,满足图中不存在这样的四个点 \(a, b, c, d\):
- 其中 \(a, b, c\) 三个点形成三元环,即 \(a \to b \to c \to a\),且它们都向 \(d\) 连边,即 \((a, b, c) \to d\)。
你需要计算每对点之间的距离之和,即 \(\displaystyle \sum_{\substack{1 \le i, j \le n \\ i \ne j}} \mathrm{dis}(i, j)\)。
其中 \(\mathrm{dis}(x, y)\) 定义为 \(x\) 到 \(y\) 需要经过的最少边数,如果 \(x\) 无法到达 \(y\) 则规定 \(\mathrm{dis}(x, y) = 614 \times n\)。
- \(3 \le n \le 8000\)。
题解
这是一道数竞题,我负责翻译官方题解并详细展开并配图。
一些前置知识和定义
众所周知,一张竞赛图,在强连通分量(SCC)缩点后,会形成一条链状 DAG。
同时,如果若干个点的导出子图中包含一个环的话,那么其中也必然包含一个三元环(用归纳法)。
记 \(\mathrm{in}(x) = \{ u \mid u \to x \}\),即所有能够到达 \(x\) 的点的集合,记 \(\deg(x) = |\mathrm{in}(x)|\),即 \(x\) 的入度。
- 引理 \(\boldsymbol{1}\):对任意一点 \(x\),\(\mathrm{in}(x)\) 中没有环,更进一步地 \([\{x\} \cup \mathrm{in}(x)]\) 中没有环。
- 证明 \(\boldsymbol{1}\):反证法,如果 \(\mathrm{in}(x)\) 中有环,那么必然有一个三元环都向 \(x\) 连边,与条件冲突。
考虑原图缩点后形成的链状 DAG,令其中点集依次为 \(S_1, S_2, \ldots , S_k\)。
即 \(S_i\) 中的所有点向 \(S_1 \sim S_{i - 1}\) 中的所有点连边,且每个 \(S_i\) 都是一个强连通分量。
- 引理 \(\boldsymbol{1.5}\):除了 \(S_1\) 外,之后所有强连通分量都含 \(1\) 个点。
- 证明 \(\boldsymbol{1.5}\):考虑 \(S_1\) 中的任意一个点 \(x\),显然 \(\mathrm{in}(x)\) 中包含所有的 \(S_2 \sim S_k\)。
- 结合引理 \(\boldsymbol{1}\),也就是说 \(S_2 \sim S_k\) 中没有环,而没有环的强连通分量必然只有 \(1\) 个点。
在算法实现中,我们每次(不断寻找)删掉一个无入度的点(即 \(S_k\) 中的唯一一个点)及其出边,直到这样的点不存在为止,剩下的点就都是 \(S_1\) 中的点。
可以很方便地计算这些「被删除的点」对答案的贡献,被删点可以 \(1\) 步到达还未被删除的点,反之则无法到达。
从现在开始我们只考虑最后的一个 \(S_1\) 的情况,也就是说假设原图是一张强连通图。
令 \(x\) 为 \(\deg\) 最大的点,如有多个任取一个。
令 \(P = \{x\} \cup \mathrm{in}(x)\),以及 \(Q = V \setminus P\)(其中 \(V\) 为所有点的集合)。
显然 \(\deg(x) = |P| - 1\),且 \(P, Q\) 均非空(且 \(P\) 去掉 \(x\) 仍然非空)(强连通图)。
- 引理 \(\boldsymbol{2}\):存在两点 \(v, u\),其中 \(v \in P, u \in Q\),且存在边 \(v \leftarrow u\)。
- 证明 \(\boldsymbol{2}\):反证法,假设不存在这样的边,也就是说 \(P\) 中所有点均向 \(Q\) 中所有点连边。
- 这是不可能的,因为如果是这样则 \(Q\) 中的每个点之 \(\deg\) 至少为 \(|P|\),与 \(\deg(x) = |P| - 1\) 且最大矛盾。
我们取满足引理 \(\boldsymbol{2}\) 中条件的一点 \(v\),令 \(R = [\mathrm{in}(v) \cap Q]\),以及 \(S = Q \setminus R\)。
特别地,\(v\) 不可能等于 \(x\),因为 \(Q\) 中所有点都不可能向 \(x\) 连边,是 \(x\) 向 \(Q\) 中所有点连边。
据此我们可以画出图形:
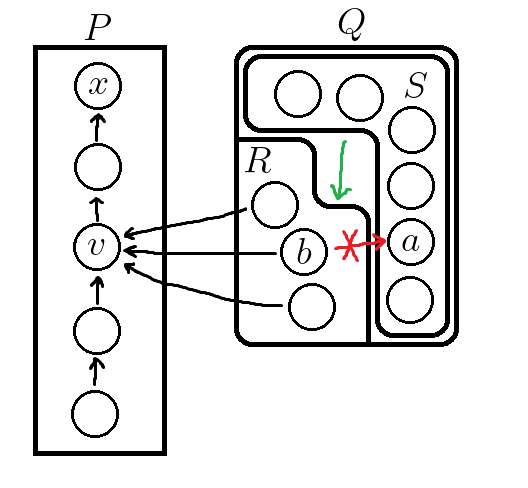
- 引理 \(\boldsymbol{3}\):对于任意 \(b \in R\) 和 \(a \in S\),必然存在 \(b \leftarrow a\),也就是说 \(S\) 中所有点向 \(R\) 中所有点连边。
- 证明 \(\boldsymbol{3}\):反证法,假设存在一对 \(b, a\) 违反此结论,也就是说 \(b \to a\)。
- 考虑 \(x, v, a, b\) 这四个点,\(b \to v \to x \to b\) 是三元环,又有 \((x, v, b) \to a\),与初始条件冲突。
据此我们可以得到:
- 引理 \(\boldsymbol{4}\):\(R\) 中无环,\(S\) 中无环。
- 证明 \(\boldsymbol{4}\):因为 \(R \subseteq \mathrm{in}(v)\) 所以显然无环,对于 \(R\) 中任意一点 \(b\) 有 \(S \subseteq \mathrm{in}(b)\) 也无环。
- 引理 \(\boldsymbol{5}\):\(P\) 中无环,\(Q\) 中无环。
- 证明 \(\boldsymbol{5}\):因为 \(P = \{x\} \cup \mathrm{in}(x)\) 所以显然无环,\(R, S\) 无环且 \(R\) 与 \(S\) 之间无环,所以 \(Q\) 也无环。
这意味着我们将图分成了两部分 \(P\) 和 \(Q\),且每部分都无环。
既然 \(P, Q\) 均有序,我们为 \(P, Q\) 中的每个点进行重编号。
令 \(P = \{P_1, P_2, \ldots , P_{|P|}\}\) 且满足对于所有 \(1 \le i1 < i2 \le |P|\) 有 \(P_{i1} \leftarrow P_{i2}\)。并且有 \(x = P_1\)。
对 \(Q\) 也进行同样的编号。
记 \(\mathrm{in}Q(P_i) = \mathrm{in}(P_i) \cap Q\),即 \(P_i\) 在 \(Q\) 中的入点集合。
记 \(\mathrm{in}P(Q_j) = \mathrm{in}(Q_j) \cap P\),即 \(Q_j\) 在 \(P\) 中的入点集合。
观察之前的图,可以发现 \(\mathrm{in}Q(v)\),也就是 \(R\),是 \(Q_{1 \sim |Q|}\) 的一个前缀。
实际上对于 \(P\) 中的任意一点 \(v\) 都成立,除非 \(\mathrm{in}Q(v) = \varnothing\),此时等同于 \(Q_{1 \sim |Q|}\) 的空前缀(引理 \(\boldsymbol{6\mathrm{a}'}\))。
所以我们有:
- 引理 \(\boldsymbol{6\mathrm{a}}\):如果 \(|\mathrm{in}Q(P_{i1})| = |\mathrm{in}Q(P_{i2})|\),那么 \(\mathrm{in}Q(P_{i1}) = \mathrm{in}Q(P_{i2})\)。
- 引理 \(\boldsymbol{6\mathrm{a}'}\):任意一个 \(\mathrm{in}Q(P_i)\) 都是 \(Q_{1 \sim |Q|}\) 的一个前缀或空前缀,前文已经证明。
- 证明 \(\boldsymbol{6\mathrm{a}}\):由前缀的唯一性可得。
事实上,对于 \(Q\) 中的点这个性质也对称地成立:
- 引理 \(\boldsymbol{6\mathrm{b}}\):如果 \(|\mathrm{in}P(Q_{j1})| = |\mathrm{in}P(Q_{j2})|\),那么 \(\mathrm{in}P(Q_{j1}) = \mathrm{in}P(Q_{j2})\)。
- 引理 \(\boldsymbol{6\mathrm{b}'}\):类似地,只要证明 \(\mathrm{in}P(Q_j)\) 是 \(P_{1 \sim |P|}\) 的一个前缀或空前缀(实际上不可能是空前缀)即可。
- 证明 \(\boldsymbol{6\mathrm{b}'}\):反证法,假设存在一点 \(c = Q_j\) 满足 \(\mathrm{in}P(c)\) 不是 \(P_{1 \sim |P|}\) 的一个前缀。
- 也就是说存在 \(d = P_{i1}, e = P_{i2}\)(其中 \(i1 < i2\))满足 \(d \notin \mathrm{in}P(c), e \in \mathrm{in}P(c)\)。
- 也就是说 \(e \to c \to d\),同时还有 \(d \leftarrow e\) 因为 \(i1 < i2\)(如有需要请读者自行画图)。
- 如果 \(\mathrm{in}Q(e) \ne \varnothing\),我们考虑任意一个 \(f \in \mathrm{in}Q(e)\),从而有 \(f \to e\)。
- 显然 \(c \notin \mathrm{in}Q(e)\),所以如果 \(f = Q_{j0}\),则有 \(j0 < j\),从而有 \(f \leftarrow c\)。
- 由于 \(j0 < j\) 且 \(c \to d\),则也有 \(f \to d\)。
- 考虑 \(f \to e \to c \to f\) 是一个三元环,且 \((e, c, f) \to d\),与初始条件冲突。
- 否则如果 \(\mathrm{in}Q(e) = \varnothing\),那么 \(e\) 必然不是 \(P_{|P|}\),因为如果是则 \(e\) 不与其他点成强连通分量。
- 考虑 \(f = Q_1\) 以及 \(g = P_{|P|}\),显然有 \(g \to (e, d)\) 和 \(f \to d\)(如有需要请读者自行画图)。
- 由于 \(\mathrm{in}Q(e) = \varnothing\),则必然有 \(e \to f\)。
- 考虑 \(\mathrm{in}Q(g)\) 必然不能为空,如果为空则 \(g = P_{|P|}\) 不与其他点成强连通分量。
- 所以因为 \(|\mathrm{in}Q(g)| \ge 1\),有 \(f \to g\)。
- 考虑 \(g \to e \to f \to g\) 是一个三元环,且 \((e, f, g) \to d\),与初始条件冲突。
- 综上所述,\(\mathrm{in}P(Q_j)\) 必然是 \(P_{1 \sim |P|}\) 的一个前缀或空前缀,引理 \(\boldsymbol{6\mathrm{b}'}\) 得证。
- 又由前缀的唯一性可得引理 \(\boldsymbol{6\mathrm{b}}\)。
我们还能得到 \(|\mathrm{in}Q(P_i)|\) 以及 \(|\mathrm{in}P(Q_j)|\) 的有序性:
- 引理 \(\boldsymbol{7}\):对于 \(1 \le i1 < i2 < |P|\),有 \(|\mathrm{in}Q(P_{i1})| \le |\mathrm{in}Q(P_{i2})|\),类似的命题对 \(|\mathrm{in}P(Q_j)|\) 也成立。
- 证明 \(\boldsymbol{7}\):反证法,假设 \(|\mathrm{in}Q(P_{i1})| > |\mathrm{in}Q(P_{i2})|\),据此有 \(\mathrm{in}Q(P_{i2}) \subsetneq \mathrm{in}Q(P_{i1})\)。
- 取出属于 \(\mathrm{in}Q(P_{i1}) \setminus \mathrm{in}Q(P_{i2})\) 的一点 \(u\)。
- 有 \(P_{i1} \leftarrow u\) 但 \(P_{i2} \to u\),也就是说 \(P_{i2}\) 属于 \(\mathrm{in}P(u)\) 但 \(P_{i1}\) 不属于,这与引理 \(\boldsymbol{6\mathrm{b}'}\) 冲突。
- 所以必然有 \(|\mathrm{in}Q(P_{i1})| \le |\mathrm{in}Q(P_{i2})|\)。
- 同理可得类似的命题对 \(|\mathrm{in}P(Q_j)|\) 也成立。
注意所有 \(Q\) 中的点都有向 \(P_{|P|}\) 的边,否则意味着某点的度数至少为 \(|P|\),与 \(\deg(x) = |P| - 1\) 且最大矛盾。
最后我们考虑 \(P, Q\) 中的点的 \(\mathrm{dis}\) 关系。
对于 \(P\) 有:
- 如果 \(i1 < i2\),则 \(\mathrm{dis}(P_{i2}, P_{i1}) = 1\)。
- 如果 \(i1 < i2\) 且 \(|\mathrm{in}Q(P_{i1})| < |\mathrm{in}Q(P_{i2})|\),则 \(\mathrm{dis}(P_{i1}, P_{i2}) = 2\)。
- 令 \(z\) 为 \(\mathrm{in}Q(P_{i2}) \setminus \mathrm{in}Q(P_{i1})\) 中任意一点,路径为 \(P_{i1} \to z \to P_{i2}\)。
- 如果 \(i1 < i2\) 且 \(|\mathrm{in}Q(P_{i1})| = |\mathrm{in}Q(P_{i2})|\),则 \(\mathrm{dis}(P_{i1}, P_{i2}) = 3\)。
- 如果 \(\mathrm{in}P(Q_1) < i1\),则路径为 \(P_{i1} \to x \to Q_1 \to P_{i2}\)。
- 否则必然有 \(i2 \le \mathrm{in}P(Q_1) < |P|\),路径为 \(P_{i1} \to Q_1 \to P_{|P|} \to P_{i2}\)。
对于 \(Q\) 有:
- 如果 \(j1 < j2\),则 \(\mathrm{dis}(Q_{j2}, Q_{j1}) = 1\)。
- 如果 \(j1 < j2\) 且 \(|\mathrm{in}P(Q_{j1})| < |\mathrm{in}P(Q_{j2})|\),则 \(\mathrm{dis}(Q_{j1}, Q_{j2}) = 2\)。
- 令 \(z\) 为 \(\mathrm{in}P(Q_{j2}) \setminus \mathrm{in}P(Q_{j1})\) 中任意一点,路径为 \(Q_{j1} \to z \to Q_{j2}\)。
- 如果 \(j1 < j2\) 且 \(|\mathrm{in}P(Q_{j1})| = |\mathrm{in}P(Q_{j2})|\),则 \(\mathrm{dis}(Q_{j1}, Q_{j2}) = 3\)。
- 路径为 \(Q_{j1} \to P_{|P|} \to x \to Q_{j2}\)。
对于 \(P, Q\) 之间的点对 \(p \in P, q \in Q\) 有:
- 如果存在 \(p \leftarrow q\),则 \(\mathrm{dis}(q, p) = 1\),\(\mathrm{dis}(p, q) = 2\),路径为 \(p \to x \to q\)。
- 如果存在 \(p \to q\),则 \(\mathrm{dis}(p, q) = 1\),\(\mathrm{dis}(q, p) = 2\),路径为 \(q \to P_{|P|} \to p\)。
综上所述:
- 对于所有 \(1 \le i1 < i2 \le |P|\),这对点对答案贡献 \(3 + [|\mathrm{in}Q(P_{i1})| = |\mathrm{in}Q(P_{i2})|]\)。
- 对于所有 \(1 \le j1 < j2 \le |Q|\),这对点对答案贡献 \(3 + [|\mathrm{in}P(Q_{j1})| = |\mathrm{in}P(Q_{j2})|]\)。
- 对于所有 \(p \in P, q \in Q\),这对点对答案贡献 \(3\)。
在算法实现中,我们可以直接处理出每个点的 \(\mathrm{in}Q\) 或 \(\mathrm{in}P\),然后使用上述结论统计答案。
下面是代码,时间复杂度为 \(\mathcal O (n^2)\):
#include <cstdio>
#include <cctype>
#include <algorithm>
#include <vector>
typedef long long LL;
const int MN = 8005;
char s[MN];
int N, deg[MN], bel[MN], num[MN];
std::vector<bool> A[MN];
int que[MN], lb, rb;
LL Ans;
int main() {
scanf("%d", &N);
for (int i = 1; i <= N; ++i) {
scanf("%s", s + 1);
A[i].resize(N + 1);
for (int j = 1; j <= N / 4; ++j) {
int x = isdigit(s[j]) ? s[j] - '0' : 10 + (s[j] - 'A');
for (int k = 0; k < 4; ++k)
A[i][4 * j - k] = x >> k & 1;
}
}
for (int i = 1; i <= N; ++i)
for (int j = 1; j <= N; ++j) if (A[i][j])
++deg[j];
int C = N;
lb = 1, rb = 0;
for (int i = 1; i <= N; ++i) if (!deg[i]) que[++rb] = i;
while (lb <= rb) {
int u = que[lb++];
bel[u] = 3;
Ans += (614ll * N + 1) * --C;
for (int i = 1; i <= N; ++i) if (A[u][i])
if (!--deg[i]) que[++rb] = i;
}
if (!C) return printf("%lld\n", Ans), 0;
int x = std::max_element(deg + 1, deg + N + 1) - deg;
for (int i = 1; i <= N; ++i) if (bel[i] != 3)
bel[i] = i == x || A[i][x] ? 1 : 2;
for (int i = 1; i <= N; ++i) if (bel[i] != 3)
for (int j = 1; j <= N; ++j) if (i != j && bel[j] != 3)
if (bel[i] != bel[j] && A[i][j]) ++num[j];
for (int i = 1; i < N; ++i) if (bel[i] != 3)
for (int j = i + 1; j <= N; ++j) if (bel[j] != 3)
Ans += 3 + (bel[i] == bel[j] && num[i] == num[j]);
printf("%lld\n", Ans);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号