AtCoder Regular Contest 125
题目传送门:AtCoder Regular Contest 125。
A - Dial Up
题意简述
给定一个长度为 \(n\) 的 01 串 \(s\),和一个长度为 \(m\) 的 01 串 \(t\)。
你有一个 01 串 \(b\),初始时为空串。你可以执行两种操作:
- 向左或者向右对 \(s\) 循环移位。
- 把 \(s\) 的首字符添加到 \(b\) 的末尾。
问是否可能能把 \(b\) 变成 \(t\),如果可行,求出最少的操作次数。
数据范围:\(1 \le n, m \le 2 \times {10}^5\)。
AC 代码
#include <cstdio>
#include <algorithm>
const int MN = 200005;
const int MM = 200005;
int N, M;
int S[MN], T[MM];
int A, B;
int main() {
scanf("%d%d", &N, &M);
for (int i = 1; i <= N; ++i)
scanf("%d", &S[i]), A += S[i];
for (int i = 1; i <= M; ++i)
scanf("%d", &T[i]), B += T[i];
if ((A == 0 && B == 0) || (A == N && B == M))
return printf("%d\n", M), 0;
if (A == 0 || A == N)
return puts("-1"), 0;
if ((S[1] == 0 && B == 0) || (S[1] == 1 && B == M))
return printf("%d\n", M), 0;
int Ans = N;
for (int i = 2; i <= N; ++i)
if (S[i] != S[1])
Ans = std::min({Ans, i - 2, N - i});
T[0] = S[1];
for (int i = 1; i <= M; ++i)
Ans += T[i] != T[i - 1];
printf("%d\n", Ans + M);
return 0;
}
无解是容易判断的:如果 \(s\) 全为一种字符,而 \(t\) 中含有至少一个另一种字符则无解。
添加字符的操作需要恰好执行 \(m\) 次,输出答案的时候加上就行了,那么就是要求出最少的循环移位次数。
如果 \(t\) 全为一种字符,而且恰好就是初始时的 \(s\) 的首字符,那就不需要循环移位,直接输出 \(m\)。
否则是需要至少一次循环移位到另一种字符上的,这一定是选取向左或向右碰到的最近的一个不同的字符。
在第一次需要循环移位的时候(也就是 \(t\) 中第一个不等于 \(s\) 的首字符的字符)移动到那里,然后接下来的每一次切换字符(即 \(t_i \ne t_{i - 1}\))只需要在那个位置周围抖动一下即可。
据此容易写出代码。
时间复杂度为 \(\mathcal O (n + m)\)。
B - Squares
题意简述
给定正整数 \(n\),求满足 \(1 \le x, y \le n\) 且 \(x^2 - y\) 为完全平方数的数对 \((x, y)\) 的数量,对 \(998244353\) 取模。
数据范围:\(1 \le n \le {10}^{12}\)。
AC 代码
#include <cstdio>
#include <cmath>
typedef long long LL;
const int Mod = 998244353;
LL N;
int main() {
scanf("%lld", &N);
LL S = 0, D = 0, Ans = 0;
for (int i = 1; ; ++i) {
S += 2 * i - 1;
D += 2;
if (S > N)
break;
Ans += (N - S) / D + 1;
}
printf("%lld\n", Ans % Mod);
return 0;
}
要让 \(x^2 - y\) 为完全平方数 \(z^2\)(\(z \ge 0\)),且 \(1 \le x, y \le n\),那么一定有 \(0 \le z < x \le n\),且 \(x^2 - z^2 \le n\)。
可以发现就是对差值 \(\le n\) 的完全平方数数对计数,对 \(x \le n\) 的限制是不必需的,因为如果存在 \(x^2 - z^2 \le n\)(满足 \(0 \le z < x\))则必然有 \(x \le \frac{n + 1}{2}\),而在数据范围下必然有 \(\frac{n + 1}{2} \le n\)。
即求出此序列中有多少对不同的数的差 \(\le n\):\([0, 1, 4, 9, 16, 25, 36, 49, \ldots ]\)。
我们考虑做此转换:将序列差分得到 \([1, 3, 5, 7, 9, \ldots ]\),这是一个等差数列。
然后即是求这个新序列中有多少段非空区间的和 \(\le n\),然后对区间长度分开考虑:
- 区间长度为 \(1\):即是求 \([1, 3, 5, 7, 9, \ldots ]\) 中有多少个数 \(\le n\)。
- 区间长度为 \(2\):即是求 \([4, 8, 12, 16, 20, \ldots ]\) 中有多少个数 \(\le n\)。
- 区间长度为 \(3\):即是求 \([9, 15, 21, 27, 33, \ldots ]\) 中有多少个数 \(\le n\)。
可以发现每一个都是等差数列,所以每个的答案是很好通过公式计算的,总答案就是每个的答案加起来。
而可以发现每个等差数列的首项都是完全平方数,所以只要枚举 \(\sqrt{n}\) 次这样的等差数列即可。
时间复杂度为 \(\mathcal O \!\left( \sqrt{n} \right)\)。
C - LIS to Original Sequence
题意简述
给出一个长度为 \(k\) 的整数序列 \(a_1, a_2, \ldots , a_k\) 满足此序列严格递增且值域在 \([1, n]\) 内。
可以证明一定存在一个 \(1 \sim n\) 的排列 \(p_1, p_2, \ldots , p_n\),满足序列 \(a\) 是它的最长上升子序列(LIS)之一。
在所有满足条件的序列 \(p\) 中,输出字典序最小的那个。
数据范围:\(1 \le k \le n \le 2 \times {10}^5\)。
AC 代码
#include <cstdio>
const int MN = 200005;
int N, K;
int B[MN];
int main() {
scanf("%d%d", &N, &K);
int j = 1;
for (int i = 1; i < K; ++i) {
int x;
scanf("%d", &x);
printf("%d ", x);
B[x] = 1;
while (B[j]) ++j;
if (j < x) {
printf("%d ", j);
B[j] = 1;
while (B[j]) ++j;
}
}
for (int i = N; i >= j; i--)
if (!B[i])
printf("%d%c", i, " \n"[i == j]);
return 0;
}
要让字典序最小,我们肯定首先贪心地进行考虑。
显然不能有 \(p_1 < a_1\),否则加入 \(p_1\) 的话就会增加 LIS 的长度。
当 \(k = 1\) 时显然只能有 \(p = [n, n - 1, \ldots , 2, 1]\),否则 LIS 长度将至少为 \(2\)。
但是我们可以证明当 \(k \ge 2\) 时,一定可以取 \(p_1 = a_1\) 而仍然存在满足条件的 \(p\)。一个证明角度如下:
- 取 \(p\) 的第 \(1\) 段为 \(a_1, a_1 - 1, \ldots , 1\)。
- 取 \(p\) 的第 \(2\) 段为 \(a_2, a_2 - 1, \ldots , a_1 + 1\)。
- ……
- 取 \(p\) 的第 \(k - 1\) 段为 \(a_{k - 1}, a_{k - 1} - 1, \ldots , a_{k - 2} + 1\)。
- 取 \(p\) 的最后一段为 \(n, n - 1, \ldots , a_k, a_k - 1, \ldots , a_{k - 1} + 1\)。
举个例子,如果 \(a = [3, 5, 6, 8]\) 而 \(n = 9\),令 \(p = [3, 2, 1, 5, 4, 6, 9, 8, 7]\)。
按照上述分段方式,每一段内都是递减的,所以 LIS 在每一段中最多取一个,而存在一种取法取得到序列 \(a\),所以满足条件。
我们已经让 \(p_1\) 满足字典序尽量小了。但是我们肯定不满足于当 \(a_1 \ge 2\) 时让 \(p_2 = a_1 - 1\)。如果此时让 \(p_2 = 1\) 会如何呢?
我们考虑上文的分段论证法,如果我们仍然可以让整个序列 \(p\) 分成 \(k\) 段,每段内都递减,而 \(a_1 \sim a_k\) 依次存在于每一段内,则此时的 \(p\) 一定是满足条件的。
所以按照此原理,显然当 \(a_1 \ge 2\) 时是可以让 \(p_2 = 1\) 的。即有:
- 如果 \(a_1 = 1\),则 \(p_1 = a_1 = 1\)。
- 如果 \(a_1 \ge 2\),则 \(p_1 = a_1\),\(p_2 = 1\)。
但是对于再下一个元素(如果 \(a_1 = 1\) 那就是 \(p_2\) 否则就是 \(p_3\))呢?
它当然可以为 \(a_2\)(如果 \(k \ge 3\)),这是由上面的构造保证的,但是它又不能在 \([a_1 + 1, a_2 - 1]\) 中,否则会增加 LIS 的长度。
那么我们要减小字典序,就是说要让它小于 \(a_1\),对于 \(a_1 = 1\) 来说这是不可能的,对于 \(a_1 \ge 2\) 来说这也是不合法的,否则 \([p_2 = 1 , p_3, a_2, a_3, \ldots , a_k]\) 就会成为更长的 LIS。
那么也就是说只能有下一个元素为 \(a_2\)(如果 \(k \ge 3\))。如果 \(k = 2\) 的话后面就只能从 \(n\) 一路递减下来了。
将这样的过程推广到 \(a\) 后面的每一项(除了最后一项 \(a_k\)),就是:
- \(p\) 的下一个元素为 \(a_i\)。
- 如果最小的可用元素小于 \(a_i\),则 \(p\) 的下一个元素为这个最小的可用元素。
- 令 \(i\) 自增 \(1\),直到 \(i = k\) 为止,此时 \(p\) 的尾部填充从 \(n\) 递减的可用元素。
这样的构造方法,由于上文的分段论证法,是合法的。而它的字典序最小性由每一步的贪心保证。
找最小可用元素维护一个指针即可。时间复杂度为 \(\mathcal O (n)\)。
D - Unique Subsequence
题意简述
给定一个长度为 \(n\) 的序列 \(a_1, a_2, \ldots , a_n\),且 \(1 \le a_i \le n\),但可以有重复元素。
求出在它之中作为子序列只出现过恰好一次的非空序列个数,对 \(998244353\) 取模。
注:只出现过恰好一次指的是仅存在唯一下标序列满足 \(a\) 对应下标的子序列为此序列。
数据范围:\(1 \le n \le 2 \times {10}^5\)。
AC 代码
#include <cstdio>
const int Mod = 998244353;
const int MN = 200005;
int N;
int l[MN], v[MN], b[MN];
inline void Add(int i, int x) {
for (; i <= N; i += i & -i)
b[i] = (b[i] + x) % Mod;
}
inline int Qur(int i) {
int s = 0;
for (; i; i -= i & -i)
s = (s + b[i]) % Mod;
return s;
}
int main() {
scanf("%d", &N);
int s = 0;
for (int i = 1; i <= N; ++i) {
int x;
scanf("%d", &x);
int f;
if (l[x]) {
f = (s - Qur(l[x] - 1) + Mod) % Mod;
Add(l[x], Mod - v[x]);
s = (s - v[x] + Mod) % Mod;
} else
f = s + 1;
Add(i, f);
s = (s + f) % Mod;
l[x] = i;
v[x] = f;
}
printf("%d\n", s);
return 0;
}
我们肯定首先考虑子序列自动机的结构。
可以发现这基本上就是要求“正着走子序列自动机得到的下标字典序最小的子序列位置”,与“反着走得到的下标字典序最大的位置”是一样的。
可以证明这个条件等价于:在子序列自动机上走每一步的时候,例如 \(p_i \to p_{i + 1}\),这之中必须满足 \(a\) 在下标区间 \([p_i + 1, p_{i + 1} - 1]\) 中不存在另一个 \(a_{p_i}\)。否则 \(p_i\) 就可以移动到那个位置上而保证还是相同的子序列,但下标集合不唯一。同时还需要保证它在子序列自动机最终到达的位置 \(p_k\) 是这个数值 \(a_{p_k}\) 的最后一次出现。
转换一下角度,这即是说 \(p_i\) 是 \(p_{i + 1}\) 的上一次出现 \(a_{p_i}\) 的位置,这和子序列自动机的“\(p_{i + 1}\) 是 \(p_i\) 的下一次出现 \(a_{p_{i + 1}}\) 的位置”是对称的。
也就是说要做 DAG 转移的话,假设当前位置是 \(\boldsymbol{i}\),上一次出现位置是 \(\boldsymbol{\mathit{last}}\),那么只接收来自 \(\boldsymbol{[\mathit{last}, i - 1]}\) 中的,是当前最后一次出现的数值的位置的转移。
我们发现这就是限定一段区间内的转移求和,并且会实时更新转移的数组(每计算一个新位置就要把上一次出现位置的转移取消掉)。
这可以通过树状数组实现。时间复杂度为 \(\mathcal O (n \log n)\)。
E - Snack
题意简述
有 \(n\) 种小球,第 \(i\) 种小球的颜色为 \(i\) 并且总共有 \(a_i\) 个。
有 \(m\) 个盒子,第 \(i\) 个盒子中,每一种颜色的小球都不能超过 \(b_i\) 个,而总小球数不能超过 \(c_i\) 个。
求最多能在盒子里装入多少小球。
数据范围:\(1 \le n, m \le 2 \times {10}^5\)。
AC 代码
#include <cstdio>
#include <algorithm>
#include <functional>
#include <climits>
typedef long long LL;
const int MN = 200005;
const int MM = 200005;
int N, M;
LL A[MN], B[MM], C[MM];
int t[MM], per[MM];
int main() {
scanf("%d%d", &N, &M);
for (int i = 1; i <= N; ++i) scanf("%lld", &A[i]);
for (int i = 1; i <= M; ++i) scanf("%lld", &B[i]);
for (int i = 1; i <= M; ++i) scanf("%lld", &C[i]);
for (int i = 1; i <= M; ++i) {
LL tmp = N - C[i] / B[i];
if (tmp < 0) tmp = 0;
t[i] = tmp;
per[i] = i;
}
std::sort(per + 1, per + M + 1, [](int i, int j) {
return t[i] < t[j];
});
std::sort(A + 1, A + N + 1);
LL Ans = LLONG_MAX;
LL SumC = 0, SumB = 0, SumA = 0;
for (int i = 1; i <= M; ++i) SumC += C[i];
int j = 1;
for (int i = 0; i <= N; ++i) {
while (j <= M && t[per[j]] == i) {
SumC -= C[per[j]];
SumB += B[per[j]];
++j;
}
if (i != 0)
SumA += A[i];
Ans = std::min(Ans, SumA + SumC + SumB * (N - i));
}
printf("%lld\n", Ans);
return 0;
}
显然这是一个网络最大流模型。如图所示:
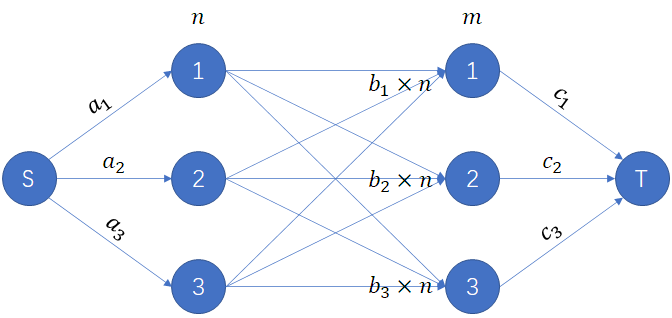
根据最大流最小割定理,我们转成最小割考虑。
如果左边割掉 \(x\) 条边,右边割掉 \(y\) 条边,那么就是左边没割掉的每个点,和右边没割掉的每个点,中间的边都要被割掉。
花费即是:
再注意到,左侧的 \(a_i\),只要确定了 \(x\),如何选取是不影响右侧的,由于是求最小割,所以一定是按 \(a_i\) 从小到大排序后取前缀。
再注意到,右侧的每个点可以自由选择与 \(T\) 之间的边是否被割,也就是可以选取 \(\min(c_i, b_i (n - x))\)。
对于一个固定的 \(i\),可以解得当 \(\displaystyle x \ge n - \frac{c_i}{b_i}\) 时才会有 \(b_i (n - x) \le c_i\),否则 \(c_i < b_i (n - x)\)。
令 \(\displaystyle t_i = \max \!\left( \left\lceil n - \frac{c_i}{b_i} \right\rceil\! , 0 \right)\! = \max \!\left( n - \!\left\lfloor \frac{c_i}{b_i} \right\rfloor\! , 0 \right)\),即如果 \(0 \le x < t_i\) 则取 \(c_i\),否则取 \(b_i (n - x)\)。
则按照 \(t_i\) 从小到大排序,从小到大枚举 \(x\),可以双指针统计答案。
时间复杂度为 \(\mathcal O (n \log n + m \log m)\)。
F - Tree Degree Subset Sum
题意简述
有一棵 \(n\) 个结点的无根树,令第 \(i\) 个结点的度数为 \(d_i\)。
求满足条件的数对 \((x, y)\) 的数量:存在一个大小为 \(x\) 的点集使得其中结点的度数之和为 \(y\)。
数据范围:\(2 \le n \le 2 \times {10}^5\)。
题意简述
#include <cstdio>
#include <functional>
typedef long long LL;
const int Inf = 0x3f3f3f3f;
const int MN = 200005;
int N, deg[MN], buk[MN];
int main() {
scanf("%d", &N);
for (int i = 1; i <= 2 * N - 2; ++i) {
int x;
scanf("%d", &x);
++deg[x];
}
for (int i = 1; i <= N; ++i)
++buk[deg[i] - 1];
static int f[MN];
for (int i = 1; i <= N - 2; ++i) f[i] = Inf;
for (int i = 1; i <= N - 2; ++i) if (buk[i]) {
int len = buk[i] + 1;
static int g[MN];
for (int j = 0; j < i; ++j) {
static int que[MN];
int head = 1, tail = 0;
for (int k = j; k <= N - 2; k += i) {
auto v = [&](int x){ return f[x] - x / i; };
while (head <= tail && v(que[tail]) > v(k)) --tail;
que[++tail] = k;
while (que[head] / i <= k / i - len) ++head;
g[k] = v(que[head]) + k / i;
}
}
for (int k = 0; k <= N - 2; ++k) f[k] = g[k];
}
LL Ans = 0;
for (int i = 0; i <= N - 2; ++i) Ans += std::max((N - f[N - 2 - i]) - f[i] + 1, 0);
printf("%lld\n", Ans);
return 0;
}
我们发现树本身并没有什么用,计算出来度数序列后就可以扔了。
这有点像是个背包问题,但是我们不可能存储两维的信息。
看起来 \(\displaystyle \sum_{i = 1}^{n} d_i = 2 n - 2\) 的性质应该是个突破口。
对于这类总和固定的正整数序列,我们知道其中不同的数的个数是 \(\mathcal O \!\left( \sqrt{n} \right)\) 的。但是对本题帮助不大。
我们知道一棵大小大于等于 \(2\) 的树一定有叶子结点。
对应到序列中就是当长度为 \(n\) 的正整数序列的总和为 \(2 n - 2\) 时一定有某个 \(d_i = 1\)。
如果从叶子结点的角度考虑,每加入一个叶子节点,可以让 \(x, y\) 均增加 \(1\),反之均减少 \(1\)。
也就是 \(y - x\) 的值是不变的,不过这样比较麻烦,我们令所有 \(d_i\) 均减少 \(1\),这样就变成非负整数序列的总和为 \(n - 2\)。
这样的话就是 \(y\) 不变,\(x\) 自由变化了。要求的东西的数量也不受影响。
关键点来了:我们猜想,对于一个固定的 \(y\) 值,对应的满足条件的 \(x\) 值要么不存在,要么形成一段连续区间。证明:
- 令这个 \(y\) 对应的最小 \(x\) 为 \(m(y)\),而最大 \(x\) 为 \(M(y)\)。
- 我们即是要证明 \(M(y) - m(y) \le 2 z\),其中 \(z\) 是 \(d_i = 0\) 的数目。
- 这是因为在 \(x\) 取值最小的方案中,权值为 \(0\) 的元素肯定一个都没取;而在 \(x\) 取值最大的方案中,权值为 \(0\) 的元素肯定全部取到了。
- 所以调整最小的方案可以取到 \([m(y), m(y) + z]\) 之间的所有 \(x\),而调整最大的方案可以取到 \([M(y) - z, M(y)]\) 之间的所有 \(x\)。
- 如果有 \(M(y) - m(y) \le 2 z\) 成立,这两个区间的并即是 \([m(y), M(y)]\)。接下来证明此式确实成立:
- 我们可以说明任意情况下都有 \(-z \le y - x \le z - 2\),于是当 \(y\) 固定时所有可能的 \(x\) 之间最多差 \(2 z - 2\)。
- 我们考虑 \(y - x\) 的意义就是每个元素的权值再减去 \(1\),即权值 \(\ge -1\) 且总和为 \(-2\) 的情况,而权值恰好为 \(-1\) 的元素有 \(z\) 个。
- 显然,权值非负的数的权值总和恰好为 \(z - 2\)(因为 \(-2 - z \cdot (-1) = z - 2\)),所以取得再多也不能超过 \(z - 2\)。
- 所以确实有 \(-z \le y - x \le z - 2\)。证毕。
那么我们只需要求出所有的 \(M(y)\) 和 \(m(y)\) 即可。这就可以通过背包求了,但是朴素做复杂度是 \(\mathcal O (n^2)\) 的。
不过注意到不同的数的个数是 \(\mathcal O \!\left( \sqrt{n} \right)\) 的,所以相当于做多重背包,用单调队列优化即可。
注意要判对于一个 \(y\) 区间为空的情况,即不存在合法的 \(x\)。
一个常数优化手段是注意到如果区间不为空的话,\(M(y) = n - m(n - 2 - y)\),所以不用做两次背包 DP。
这题中好像二进制分组优化多重背包比直接单调队列跑得快,虽然理论上多一个 \(\log\),我对此并不太确定是什么原理。jiangly 指正这里不多 \(\log\),因为总和为 \(s\) 的正整数序列 \(a\) 的 \(\sum \log c_k\) 为 \(\mathcal O \!\left( \sqrt{n} \right)\),其中 \(c_k\) 表示 \(a_i = k\) 的个数。
时间复杂度:\(\mathcal O \! \left( n \sqrt{n} \right)\)。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号