AtCoder Grand Contest 019
题目传送门:AtCoder Grand Contest 019。
A - Ice Tea Store
如果买两瓶 250mL 的冰红茶比买一瓶 500mL 的冰红茶更便宜,就更新它。
同理,用 500mL 的更新 1L 的,用 1L 的更新 2L 的。
最终答案是 \(\lfloor N / 2 \rfloor \times S + (N \bmod 2) \times D\)。
#include <cstdio>
typedef long long LL;
int main() {
int Q, H, S, D; LL N;
scanf("%d%d%d%d%lld", &Q, &H, &S, &D, &N);
if (H > 2 * Q) H = 2 * Q;
if (S > 2 * H) S = 2 * H;
if (D > 2 * S) D = 2 * S;
printf("%lld\n", N / 2 * D + N % 2 * S);
return 0;
}
B - Reverse and Compare
如果选取的要 reverse 的区间 \([l, r]\),它两端点的 \(A_l = A_r\),则产生的结果就会与区间 \([l + 1, r - 1]\) 相同了。
而每个 \(A_l \ne A_r\) 的区间 reverse 后,显然是两两不同的(考虑最左侧与原串不同的位置,即为 \(l\),同理确定 \(r\))。
那么就是统计 \(A_l \ne A_r\) 的数对个数,对每个字母开个桶统计即可。
#include <cstdio>
typedef long long LL;
const int MN = 200005, Sig = 26;
char s[MN];
int buk[Sig];
LL Ans;
int main() {
scanf("%s", s + 1);
for (int i = 1; s[i]; ++i)
Ans += i - ++buk[s[i] - 'a'];
printf("%lld\n", Ans + 1);
return 0;
}
C - Fountain Walk
显然,因为 \(100\) 米太长了,不应该走出起点和终点确定的矩形内。
那么我们考虑起点到终点的路径,我们要尽量最大化经过的 \(1 / 4\) 圆的数量,但与此同时要减少 \(1 / 2\) 圆的数量。
我们考虑计算出最多能经过的圆的数量,这可以通过求 LIS(最长上升子序列)得到。
假设会经过 \(k\) 个圆,经过的这 \(k\) 个圆都可以是 \(1 / 4\) 圆吗?
不一定,如果 \(k = \min(|x_2 - x_1|, |y_2 - y_1|) + 1\) 的话,是必须有一个圆要变成 \(1 / 2\) 圆的。
否则可以证明一定可以让这 \(k\) 个圆都成为 \(1 / 4\) 圆。其实还挺坑的,我本来以为只有起点和终点在同一直线上时才会有 \(1 / 2\) 圆。
#include <cstdio>
#include <cmath>
#include <algorithm>
typedef double r64;
const r64 PI = acos(-1);
const r64 C1 = 5 * (PI - 4);
const r64 C2 = 10 * (PI - 2);
const int Inf = 0x3f3f3f3f;
const int MN = 200005;
int sx, sy, tx, ty, N, K, px[MN], py[MN], p[MN];
r64 Ans;
int f[MN];
int main() {
scanf("%d%d%d%d%d", &sx, &sy, &tx, &ty, &N);
Ans = 100ll * (abs(tx - sx) + abs(ty - sy));
if (sx > tx) std::swap(sx, tx), std::swap(sy, ty);
int rev = sy > ty;
if (rev) std::swap(sy, ty);
for (int i = 1, x, y; i <= N; ++i) {
scanf("%d%d", &x, &y);
if (x < sx || tx < x || y < sy || ty < y) continue;
if (rev) y = -y;
px[++K] = x, py[K] = y, p[K] = K;
}
std::sort(p + 1, p + K + 1, [](int i, int j) { return px[i] < px[j]; });
int num = 0;
f[0] = -Inf;
for (int i = 1; i <= K; ++i) f[i] = Inf;
for (int i = 1; i <= K; ++i) {
int v = py[p[i]];
int j = std::lower_bound(f, f + K + 1, v) - f;
if (num < j) num = j;
f[j] = v;
}
if (num == std::min(tx - sx, ty - sy) + 1) Ans += (num - 1) * C1 + C2;
else Ans += num * C1;
printf("%.15lf\n", Ans);
return 0;
}
D - Shift and Flip
令 \(N = |A| = |B|\)。
注意到 \(N \le 2000\),我们只需要搞出一个 \(\tilde{\mathcal O} (N^2)\) 的做法就行。
如果 \(B\) 是全 \(0\) 串,特判一下即可,接下来假设 \(B\) 至少有一个 \(1\)。
考虑我们会把 \(A\) 转来转去,假设往右循环移位记作 \(+1\),往左记作 \(-1\)。
我们可以枚举最终 \(A\) 到达的位置(就是说,相对初始位置转了多少个单位,用 \(\pm 1\) 算),假设为 \(r\)。
注意,因为始终可以构造 \(2 N - 1\) 步内变成 \(B\) 的操作方法(转一圈儿,再对每个位置都取反一次,因为卡不满所以减 \(1\)):
我们只需在 \([1 - 2 N, 2 N - 1]\) 内枚举 \(r\) 即可。
枚举了 \(r\) 后,我们就得到了 \(A\) 中的哪些位置与 \(B\) 不同,是需要取反的,对这些位置我们可以预处理出两个值:
如果往向右循环移位,需要移多少位才能到达一个 \(B\) 中的 \(1\),从而进行取反操作,同理可以处理出只往左循环移位的情况。
如果向右、向左中至少有一个已经落在了我们从 \(0\) 到达 \(r\) 的区间内了,就不需要花费额外的移位代价,只要多操作一次就行。
否则不仅要操作一次,还要产生额外的移位代价,如果需要向右的长度比右端点还往右,处理出多了多长。
如果选取了该位置要往右循环移位然后取反,移位时就至少要超出原右端点,超出这个长度这么多。
向左的长度同理,可以处理出来会多多少。
也就是对每个这样的位置,有两个值:向左会多多少,向右会多多少。
每个位置要选择它是向左还是向右,而最终向左的长度,就是选取向左的位置中,向左的长度的最大值。向右同理。
而额外的移动代价,就是最终向左向右的长度之和,再乘以 \(2\)。
总之我们需要最小化向左向右的长度之和。这个的话,对于某一维排个序,然后做前缀后缀最大值就行了。
排序用基数排序的话,时间复杂度就是 \(\mathcal O (N^2)\) 的,代码中直接 sort 了,时间复杂度会多一个 \(\log N\)。
#include <cstdio>
#include <cstring>
#include <algorithm>
const int Inf = 0x3f3f3f3f;
const int MN = 2005;
int N;
char s[MN], t[MN];
int A[MN], B[MN], L[MN], R[MN], dl[MN], dr[MN], p[MN], suf[MN];
inline int Solve(int r) {
int ret = 0, lb = 0, rb = 0, K = 0;
if (r >= 0) ret = r, rb = r;
else ret = -r, lb = r;
for (int i = 1; i <= N; ++i) {
if (A[i] == B[(((i + r) % N + N - 1) % N) + 1]) continue;
++ret;
if (lb <= L[i] || R[i] <= rb) continue;
dl[++K] = lb - L[i], dr[K] = R[i] - rb, p[K] = K;
}
std::sort(p + 1, p + K + 1, [](int i, int j) { return dl[i] < dl[j]; });
suf[K + 1] = 0;
for (int i = K; i >= 1; --i) suf[i] = std::max(suf[i + 1], dr[p[i]]);
int mnv = suf[1];
for (int i = 1, val = 0; i <= K; ++i)
val = std::max(val, dl[p[i]]),
mnv = std::min(mnv, val + suf[i + 1]);
return ret + 2 * mnv;
}
int main() {
scanf("%s%s", s + 1, t + 1), N = strlen(s + 1);
int ok = 0;
for (int i = 1; i <= N; ++i) if (t[i] == '1') ok = 1;
if (!ok) {
for (int i = 1; i <= N; ++i) if (s[i] == '1') return puts("-1"), 0;
return puts("0"), 0;
}
for (int i = 1; i <= N; ++i)
A[i] = s[i] - '0', B[i] = t[i] - '0';
for (int i = 1, x, y; i <= N; ++i) {
x = y = i;
while (!B[x]) --L[i], x = x > 1 ? x - 1 : N;
while (!B[y]) ++R[i], y = y < N ? y + 1 : 1;
}
int Ans = Inf;
for (int r = 1 - 2 * N; r <= 2 * N - 1; ++r)
Ans = std::min(Ans, Solve(r));
printf("%d\n", Ans);
return 0;
}
E - Shuffle and Swap
一个极其重要的转化:
- 与其分别对 \(a\) 序列和 \(b\) 序列进行随机排列,得到 \({(k!)}^2\) 种情况;
- 不如看作:先钦定 \(a\) 中的每个元素和 \(b\) 中的哪个元素配对,这里 \(k!\) 种情况,再确定每一对之间的顺序,这里又 \(k!\) 种情况。
现在我们考虑钦定了配对的关系(也就是每次会把 \(A\) 中的哪两个交换)后,统计合法的「每一对执行的先后顺序」的数量。
我们考虑一张图:只要是 \(a_i\) 与 \(b_j\) 配对了,这张图中就从 \(a_i\) 向 \(b_j\) 连一条有向边。
这张图中有连边的点,就是那些在 \(A\) 或 \(B\) 中为 \(1\) 的位置,如果均为 \(0\) 那肯定没有边与其相连了。
我们考虑如果一个位置 \(p\),如果 \(A_p, B_p\) 均为 \(1\),那么这个点在图中就是出度入度均为 \(1\)。
如果 \(A_p = 1\) 但是 \(B_p = 0\) 的话,那就是只有出度为 \(1\),类似也有一些点入度为 \(1\)。
也就是说:抛开孤立点,这张图其实是由若干个环和链构成的。
此时我们再来考虑「合法的『每一对执行的先后顺序』的数量」应该如何计算。
对于环中的边,谁先执行是完全无影响的,因为每次执行都是交换两个 \(A\) 中的 \(1\) 罢了,没有任何意义。
对于链中的边,此时必须是要从链尾到链首的顺序执行,只有唯一的一种执行方案。
我们考虑一下 \(A_p = 1\) 且 \(B_p = 0\) 的位置个数,假设为 \(e\),显然 \(A_p = 0\) 且 \(B_p = 1\) 的位置个数也为 \(e\)。
也就是图中会有 \(e\) 条链,链首和链尾的标号已经被钦定了,但是链的中转节点和环上的点的标号还没确定。
那么我们令链的标号被其起点确定,对每个起点钦定一个终点,乘一个 \(e!\) 到答案中。
那么我们按照标号顺序确定每一条链中的点,然后再考虑若干个环中的点即可。
若一条链内部有 \(i\) 个点,那就有 \(i!\) 种排列方式,而且在 \(i + 1\) 条边中,只有一种执行顺序是合法的。
若一个环有 \(i\) 个点,就有 \((i - 1)!\) 种排列方式(圆排列),而且在 \(i\) 条边中,\(i!\) 种执行顺序都是合法的。
注意合并这些连通分量的时候,是需要乘多重组合数的,考虑用指数型生成函数的方法处理:
-
链的生成函数:\(\displaystyle \sum_{i = 0}^{\infty} \frac{i! \times 1 \times z^i}{i! \times (i + 1)!} = \sum_{i = 0}^{\infty} \frac{z^i}{(i + 1)!} = \frac{\mathrm{e}^z - 1}{z}\)。
-
环的生成函数:\(\displaystyle \sum_{i = 1}^{\infty} \frac{(i - 1)! \times i! \times z^i}{i! \times i!} = \sum_{i = 1}^{\infty} \frac{z^i}{i} = - \ln (1 - z)\)。
其中链之间是有序的,且必须取恰好 \(e\) 个,应该取 \(e\) 次幂。而环之间是无序的,数量也不限,应该取 \(\exp\)。
所以答案的生成函数应该是 \(\displaystyle \left( \frac{\mathrm{e}^z - 1}{z} \right)^e \exp(- \ln (1 - z)) = \frac{1}{1 - z} \left( \frac{\mathrm{e}^z - 1}{z} \right)^e\)。
而出度入度均为 \(1\) 的点的数量就是 \(k - e\) 个,所以最终答案(乘上之前的 \(e!\))即是 \(\displaystyle e! (k - e)! k! \left[ z^{k - e} \right] \frac{1}{1 - z} \left( \frac{\mathrm{e}^z - 1}{z} \right)^e\)。
可以使用多项式快速幂在 \(\mathcal O (N \log^2 N)\)(二进制拆分卷积快速幂)或 \(\mathcal O (N \log N)\)(多项式 \(\ln, \exp\))的时间内解决。
#include <cstdio>
#include <cstring>
#include <algorithm>
typedef long long LL;
const int Mod = 998244353;
const int G = 3, iG = 332748118;
const int MS = 1 << 15;
inline int qPow(int b, int e) {
int a = 1;
for (; e; e >>= 1, b = (LL)b * b % Mod)
if (e & 1) a = (LL)a * b % Mod;
return a;
}
inline int gInv(int b) { return qPow(b, Mod - 2); }
int Inv[MS], Fac[MS], iFac[MS];
inline void Init(int N) {
Fac[0] = 1;
for (int i = 1; i <= N; ++i) Fac[i] = (LL)Fac[i - 1] * i % Mod;
iFac[N] = gInv(Fac[N]);
for (int i = N; i >= 1; --i) iFac[i - 1] = (LL)iFac[i] * i % Mod;
for (int i = 1; i <= N; ++i) Inv[i] = (LL)Fac[i - 1] * iFac[i] % Mod;
}
inline int Binom(int N, int M) {
if (M < 0 || M > N) return 0;
return (LL)Fac[N] * iFac[M] % Mod * iFac[N - M] % Mod;
}
int Sz, InvSz, R[MS];
inline int getB(int N) { int Bt = 0; while (1 << Bt < N) ++Bt; return Bt; }
inline void InitFNTT(int N) {
int Bt = getB(N);
if (Sz == (1 << Bt)) return ;
Sz = 1 << Bt, InvSz = Mod - (Mod - 1) / Sz;
for (int i = 1; i < Sz; ++i) R[i] = R[i >> 1] >> 1 | (i & 1) << (Bt - 1);
}
inline void FNTT(int *A, int Ty) {
for (int i = 0; i < Sz; ++i) if (R[i] < i) std::swap(A[R[i]], A[i]);
for (int j = 1, j2 = 2; j < Sz; j <<= 1, j2 <<= 1) {
int wn = qPow(~Ty ? G : iG, (Mod - 1) / j2), w, X, Y;
for (int i = 0, k; i < Sz; i += j2) {
for (k = 0, w = 1; k < j; ++k, w = (LL)w * wn % Mod) {
X = A[i + k], Y = (LL)w * A[i + j + k] % Mod;
A[i + k] -= (A[i + k] = X + Y) >= Mod ? Mod : 0;
A[i + j + k] += (A[i + j + k] = X - Y) < 0 ? Mod : 0;
}
}
}
if (!~Ty) for (int i = 0; i < Sz; ++i) A[i] = (LL)A[i] * InvSz % Mod;
}
inline void PolyConv(int *_A, int N, int *_B, int M, int *_C, int tN = -1) {
if (tN == -1) tN = N + M - 1;
static int A[MS], B[MS];
InitFNTT(N + M - 1);
for (int i = 0; i < N; ++i) A[i] = _A[i];
for (int i = N; i < Sz; ++i) A[i] = 0;
for (int i = 0; i < M; ++i) B[i] = _B[i];
for (int i = M; i < Sz; ++i) B[i] = 0;
FNTT(A, 1), FNTT(B, 1);
for (int i = 0; i < Sz; ++i) A[i] = (LL)A[i] * B[i] % Mod;
FNTT(A, -1);
for (int i = 0; i < tN; ++i) _C[i] = A[i];
}
inline void PolyInv(int *_A, int N, int *_B) {
static int A[MS], B[MS], tA[MS], tB[MS];
for (int i = 0; i < N; ++i) A[i] = _A[i];
for (int i = N, Bt = getB(N); i < 1 << Bt; ++i) A[i] = 0;
B[0] = gInv(A[0]);
for (int L = 1; L < N; L <<= 1) {
int L2 = L << 1, L4 = L << 2;
InitFNTT(L4);
for (int i = 0; i < L2; ++i) tA[i] = A[i];
for (int i = L2; i < Sz; ++i) tA[i] = 0;
for (int i = 0; i < L; ++i) tB[i] = B[i];
for (int i = L; i < Sz; ++i) tB[i] = 0;
FNTT(tA, 1), FNTT(tB, 1);
for (int i = 0; i < Sz; ++i) tB[i] = tB[i] * (2 - (LL)tA[i] * tB[i] % Mod + Mod) % Mod;
FNTT(tB, -1);
for (int i = 0; i < L2; ++i) B[i] = tB[i];
}
for (int i = 0; i < N; ++i) _B[i] = B[i];
}
inline void PolyLn(int *_A, int N, int *_B) {
static int tA[MS], tB[MS];
for (int i = 1; i < N; ++i) tA[i - 1] = (LL)_A[i] * i % Mod;
PolyInv(_A, N - 1, tB);
InitFNTT(N + N - 3);
for (int i = N - 1; i < Sz; ++i) tA[i] = 0;
for (int i = N - 1; i < Sz; ++i) tB[i] = 0;
FNTT(tA, 1), FNTT(tB, 1);
for (int i = 0; i < Sz; ++i) tA[i] = (LL)tA[i] * tB[i] % Mod;
FNTT(tA, -1);
_B[0] = 0;
for (int i = 1; i < N; ++i) _B[i] = (LL)tA[i - 1] * Inv[i] % Mod;
}
inline void PolyExp(int *_A, int N, int *_B) {
static int A[MS], B[MS], tA[MS], tB[MS];
for (int i = 0; i < N; ++i) A[i] = _A[i];
for (int i = N, Bt = getB(N); i < 1 << Bt; ++i) A[i] = 0;
B[0] = 1;
for (int L = 1; L < N; L <<= 1) {
int L2 = L << 1, L4 = L << 2;
for (int i = L; i < L2; ++i) B[i] = 0;
PolyLn(B, L2, tA);
InitFNTT(L4);
for (int i = 0; i < L2; ++i) tA[i] = (!i + A[i] - tA[i] + Mod) % Mod;
for (int i = L2; i < Sz; ++i) tA[i] = 0;
for (int i = 0; i < L; ++i) tB[i] = B[i];
for (int i = L; i < Sz; ++i) tB[i] = 0;
FNTT(tA, 1), FNTT(tB, 1);
for (int i = 0; i < Sz; ++i) tA[i] = (LL)tA[i] * tB[i] % Mod;
FNTT(tA, -1);
for (int i = 0; i < L2; ++i) B[i] = tA[i];
}
for (int i = 0; i < N; ++i) _B[i] = B[i];
}
const int MN = 10005;
int N, k, e;
char A[MN], B[MN];
int F[MN];
int main() {
scanf("%s%s", A + 1, B + 1), N = strlen(A + 1);
for (int i = 1; i <= N; ++i) A[i] == '1' ? ++k, B[i] == '0' ? ++e : 0 : 0;
Init(k + 1);
for (int i = 0; i <= k - e; ++i) F[i] = iFac[i + 1];
PolyLn(F, k - e + 1, F);
for (int i = 0; i <= k - e; ++i) F[i] = (LL)F[i] * e % Mod;
PolyExp(F, k - e + 1, F);
int Ans = 0;
for (int i = 0; i <= k - e; ++i) Ans = (Ans + F[i]) % Mod;
printf("%lld\n", (LL)Ans * Fac[e] % Mod * Fac[k] % Mod * Fac[k - e] % Mod);
return 0;
}
F - Yes or No
我们将 \(\displaystyle \binom{N + M}{N}\) 种不同的答案序列,看成一条折线从 \((N, M)\) 走到 \((0, 0)\) 的方案数(每步只能向下或者向左走一格)。
最佳策略是:此时已知 Yes 有 \(a\) 个而 No 有 \(b\) 个,若 \(a > b\) 回答 Yes,若 \(a < b\) 回答 No,否则 \(a = b\) 回答 Yes/No 均可。
我们用横坐标表示 \(a\),纵坐标表示 \(b\),下图显示的就是当 \(a = 13\) 且 \(b = 8\) 时的情况。
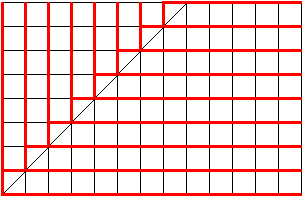
可以发现,此时若折线向左,就相当于是本题答案为 Yes,向下则本题答案为 No。
同时,图中还有一条线:被方程 \(a = b\) 确定的斜线。
如果此时位置不在斜线上,则我们的最佳策略指出,将会回答更靠近斜线的答案。否则不妨回答 Yes。
如果回答的答案恰好与折线的走势相同,则相当于答对了一题,否则答错。
但是无论如何我们的位置,都会同折线一起前进一步,可能更靠近斜线也可能更远离斜线。
那么此时就等价于:折线经过的红色线段数量,就是我们会在这条折线对应的答案序列上产生的得分。
我们对所有的折线,将这个数值求和,然后除以 \(\displaystyle \binom{N + M}{N}\) 就是最终答案了。
折线经过的红色线段数量如何统计呢?我们不妨假设 \(N \ge M\),也就是出发点在斜线下方的情况。
此时如果折线到达了斜线的上方,我们强行把到达斜线上方的那一部分,给折回来,折到斜线下方。
这样一变换,折线在斜线上方的部分,经过的红色线段的数量,可以发现大部分都是没变化的。
但这只是除了刚好从斜线上往左走的那些,也就是,这样折回来,损失了刚好从斜线上往左走的那一部分。
我们先不考虑那些损失,对于从未到达斜线上方的折线,显然,经过的红色线段数量恰好为 \(N\)!
那么我们只需统计刚好从斜线上往左走的期望次数。
显然只需要对斜线上的每个点,统计折线经过它的概率,乘上 \(1 / 2\)(往左走的概率)即可。
最终答案就是 \(N\) 加上这个「刚好从斜线上往左走的期望次数」。
#include <cstdio>
#include <algorithm>
typedef long long LL;
const int Mod = 998244353, Inv2 = (Mod + 1) / 2;
const int MN = 1000005;
inline int qPow(int b, int e) {
int a = 1;
for (; e; e >>= 1, b = (LL)b * b % Mod)
if (e & 1) a = (LL)a * b % Mod;
return a;
}
inline int gInv(int b) { return qPow(b, Mod - 2); }
int Fac[MN], iFac[MN];
inline void Init(int N) {
Fac[0] = 1;
for (int i = 1; i <= N; ++i) Fac[i] = (LL)Fac[i - 1] * i % Mod;
iFac[N] = gInv(Fac[N]);
for (int i = N; i >= 1; --i) iFac[i - 1] = (LL)iFac[i] * i % Mod;
}
inline int Binom(int N, int M) {
if (M < 0 || M > N) return 0;
return (LL)Fac[N] * iFac[M] % Mod * iFac[N - M] % Mod;
}
inline int Calc(int N, int M) {
return Binom(N + M, N);
}
int N, M;
int main() {
scanf("%d%d", &N, &M);
if (N < M) std::swap(N, M);
Init(N + M);
int Ans = 0;
for (int i = 1; i <= M; ++i) Ans = (Ans + (LL)Calc(i, i) * Calc(N - i, M - i)) % Mod;
Ans = (LL)Ans * gInv(Calc(N, M)) % Mod;
printf("%lld\n", (N + (LL)Ans * Inv2) % Mod);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号