AtCoder Grand Contest 007
题目传送门:AtCoder Grand Contest 007。
A - Shik and Stone
井号个数必须等于 \(N + M - 1\)。
#include <cstdio>
int N, M, C;
int main() {
scanf("%d%d", &N, &M);
for (int i = 1; i <= N * M; ++i) {
char s[2];
scanf("%1s", s);
C += *s == '#';
}
puts(C == N + M - 1 ? "Possible" : "Impossible");
return 0;
}
B - Construct Sequences
令 \(a_i = N \cdot i\),并且 \(a_{p_i} + b_{p_i} + 1 = a_{p_{i + 1}} + b_{p_{i + 1}}\)。合理安排 \(b\) 的值即可。
#include <cstdio>
const int V = 500000000;
const int MN = 20005;
int N, A[MN];
int main() {
scanf("%d", &N);
for (int i = 1, x; i <= N; ++i) scanf("%d", &x), A[x] = i;
for (int i = 1; i <= N; ++i) printf("%d%c", N * i, " \n"[i == N]);
for (int i = 1; i <= N; ++i) printf("%d%c", V + A[i] - N * i, " \n"[i == N]);
return 0;
}
C - Pushing Balls
一开始时,相邻两个洞与球之间的距离,是等差数列。令首项为 \(a\),公差为 \(b\)。
根据期望的线性性,我们考虑求出第一次操作后,规模小了 \(1\) 的情况的相邻两个洞与球之间的距离的期望值。
一通推导发现还是等差数列,并且有公式:\(\left< a', b' \right> = \left< ((2 n + 2) a + 5 b) / (2 n), (n + 2) b / n \right>\)。
所以每次求出第一次操作后时的代价,和操作后的 \(a, b\) 然后递归进规模减去 \(1\) 的情况即可。
#include <cstdio>
int N;
double A, B, Ans;
int main() {
scanf("%d%lf%lf", &N, &A, &B);
for (int i = N; i >= 1; --i) {
Ans += A + (2 * i - 1) * B / 2;
A = ((2 * i + 2) * A + 5 * B) / (2 * i);
B = B * (i + 2) / i;
}
printf("%.10lf\n", Ans);
return 0;
}
D - Shik and Game
一定是一直往右走,直到走到某只熊,然后往回走,到第一个还未被捡的金币处,等到金币被熊给出后,一直向右走到回头的位置。
我们考虑对着这个过程 DP。答案一定是 \(E\) 加一个值,这个值即是把所有熊划分成若干段,每段代价为 \(\max(2 (x_r - x_\ell), T)\)。
令 \(\mathrm{f}[i]\) 表示把前 \(i\) 个分成若干段的最小总代价,朴素的 DP 是 \(\mathcal O (n^2)\) 的。
注意到对于每个 \(i\),一个前缀的 \(j\) 向它转移的代价是 \(2 (x_i - x_{j + 1})\),一个后缀的 \(j\) 向它转移的代价是 \(T\)。
然而 \(\mathrm{f}[i]\) 显然是单调递增的,所以后缀的 \(j\) 直接取最前一个进行转移即可。
对于前缀的 \(j\),记 \(\mathrm{g}[j] = \mathrm{f}[j] - 2 x_{j + 1}\),于是就有 \(\mathrm{f}[i] \gets \mathrm{g}[j] + 2 x_i\)。
前缀的长度是单调非严格递增的,可以双指针确定。
#include <cstdio>
#include <algorithm>
typedef long long LL;
const LL Infll = 0x3f3f3f3f3f3f3f3f;
const int MN = 200005;
int N, E, T, A[MN];
LL f[MN], g[MN];
int main() {
scanf("%d%d%d", &N, &E, &T);
for (int i = 1; i <= N; ++i) scanf("%d", &A[i]);
g[0] = Infll;
for (int i = 1, j = 1; i <= N; ++i) {
while (2 * (A[i] - A[j]) > T) ++j;
f[i] = std::min(f[j - 1] + T, 2 * A[i] + g[j - 1]);
g[i] = std::min(g[i - 1], f[i - 1] - 2 * A[i]);
}
printf("%lld\n", E + f[N]);
return 0;
}
E - Shik and Travel
(我们记 \(w_u\) 为节点 \(u\) 到其双亲节点的边的权值)
首先观察到必然是先走到其中一个子树,把这个子树全走完,再去另一个子树。要不然就会有一条边被经过四次或以上。
我们考虑先二分答案 \(\mathrm{ans}\),然后去判断是否存在每次从叶子跳到另一个叶子时距离不超过 \(\mathrm{ans}\) 的路径。
这引出一个树形 DP:令 \(\mathrm{f}[u][x][y]\) 表示从 \(u\) 出发到每个 \(u\) 子树中的叶子再回到 \(u\),第一次距离为 \(x\),最后一次距离为 \(y\) 是否可行。
合并两个孩子时就可以枚举进入子树的先后顺序,以及两边 DP 值为 \(1\) 的状态进行合并转移。
也就是:\(\mathrm{f}[v_1][a][b]\) 和 \(\mathrm{f}[v_2][c][d]\) 如果都为 \(1\),并且 \(b + c + w_{v_1} + w_{v_2} \le \mathrm{ans}\),就可以转移到 \(\mathrm{f}[u][a + w_{v_1}][d + w_{v_2}]\)。
但是这样状态数太多了,我们考虑记 \(S_u = \{ (a, b) \mid \mathrm{f}[u][a][b] = 1 \}\),然后继承子节点的集合 \(S_{v_1}\) 和 \(S_{v_2}\) 进行转移。
当然这样状态数还是很多,我们考虑 \((a, b), (a', b') \in S\),并且 \(a \le a'\),\(b \le b'\),则 \((a', b')\) 是可以被忽略的。
我们只保留在这样的条件下不会被忽略的 \((a, b)\) 对,如果有 \((a_1, b_1)\) 和 \((a_2, b_2)\) 两对,且 \(a_1 < a_2\),则有 \(b_1 > b_2\)。
合并子树时考虑 \(v_1\) 给出的一对 \((a, b)\),对于 \(v_2\) 给出的 \((c, d)\),如果 \(b + c \le \mathrm{ans} - w_{v_1} - w_{v_2}\),就可转移到 \((a + w_{v_1}, d + w_{v_2})\)。
或者如果 \(a + d \le \mathrm{ans} - w_{v_1} - w_{v_2}\),也可转移到 \((c + w_{v_1}, b + w_{v_2})\)。
例如第一种转移,要让转移到的 \(d\) 尽量小,也就是 \(c\) 尽量大,但是如果 \(c\) 太大就不满足条件了,所以要选满足条件的尽量大的 \(c\)。
而第二种就是选满足条件的尽量大的 \(d\)。
所以每个 \((a, b)\) 只会导出最多两个数对贡献给双亲结点。
也就是:\(|S_u| \le 2 \min(|S_{v_1}|, |S_{v_2}|)\)。
根据重链剖分那套结论,我们就有 \(\displaystyle \sum_u |S_u| = \mathcal O (N \log N)\)。
只要保证转移时的复杂度是线性的即可,显然双指针即可做到线性,注意用归并排序。
总复杂度 \(\mathcal O (N \log N \log \mathrm{ans})\)。
#include <cstdio>
#include <algorithm>
typedef long long LL;
const int MN = 1 << 17 | 7;
int N, p[MN], v[MN], d[MN];
struct dat {
LL x, y;
dat() { x = y = 0; }
dat(LL a, LL b) { x = a, y = b; }
} tmp1[MN], tmp2[MN];
std::vector<dat> f[MN];
int vis[MN];
inline bool check(LL w) {
for (int i = 1; i <= N; ++i)
if (d[i]) f[i].clear(), vis[i] = 0;
for (int u = N; u >= 2; --u) if (vis[p[u]]) {
int a = u, c = p[u], b = vis[c];
if (f[a].size() > f[b].size()) std::swap(a, b);
int na = f[a].size(), nb = f[b].size(), k1 = 0, k2 = 0;
LL t = w - v[a] - v[b];
for (int i = 0, j1 = -1, j2 = 0; i < na; ++i) {
while (j1 + 1 < nb && f[a][i].y + f[b][j1 + 1].x <= t) ++j1;
while (j2 < nb && f[a][i].x + f[b][j2].y > t) ++j2;
if (j1 >= 0) tmp1[++k1] = dat(f[a][i].x + v[a], f[b][j1].y + v[b]);
if (j2 < nb) tmp2[++k2] = dat(f[b][j2].x + v[b], f[a][i].y + v[a]);
}
int d1 = 1, d2 = 1;
while (d1 <= k1 || d2 <= k2) {
dat g = d2 > k2 || (d1 <= k1 && tmp1[d1].x <= tmp2[d2].x) ? tmp1[d1++] : tmp2[d2++];
if (f[c].empty()) f[c].push_back(g);
else if (f[c].back().x == g.x && f[c].back().y >= g.y) f[c].back() = g;
else if (f[c].back().y > g.y) f[c].push_back(g);
}
if (f[c].empty()) return 0;
} else vis[p[u]] = u;
return 1;
}
int main() {
scanf("%d", &N);
for (int i = 2; i <= N; ++i)
scanf("%d%d", &p[i], &v[i]), d[p[i]] = 1;
for (int i = 1; i <= N; ++i) if (!d[i]) f[i].resize(1);
LL lb = 0, rb = (N - 1ll) << 17, mid, ans = -1;
while (lb <= rb) {
mid = (lb + rb) >> 1;
if (check(mid)) ans = mid, rb = mid - 1;
else lb = mid + 1;
}
printf("%lld\n", ans);
return 0;
}
F - Shik and Copying String
我们观察转移的过程:
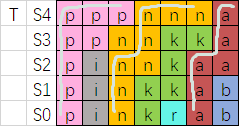
最终在 \(T\) 中的连续段,我们在它们上画线,并顺着相同的字母延伸下来回到 \(S_0\)。
为了使得线条的高度最小,我们考虑这样一个贪心做法:
在 \(T\) 中从后往前贪心,对于每个同字母连续段 \([\ell, r]\),找到在 \(\ell\) 或 \(\ell\) 之前的,最近的还未被画线的相同字母的 \(S_0\) 的位置 \(j\)。
从 \(r\) 画到 \(\ell\),然后贪心地从 \(\ell\) 开始,保证不和之前的线以及 \(S_0\) 相交,尽量地往下画,如果不行了再往左画,直到画到 \(S_0[j]\) 上方:
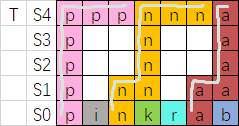
这样似乎只能对一个 \(T = S_k\) 进行 check,于是导出一个二分答案的做法,不过我们也可以轻松地将其改写为直接求答案的做法:
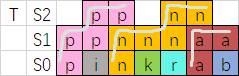
通过维护当前每个位置的最高的线的高度 \(h\),我们可以在 \(\mathcal O (N^2)\) 的时间内维护这个贪心并求出答案。
也就是:一开始 \(h\) 全为 \(0\);假设处理的是 \([\ell, r]\) 以及 \(j\),令 \(i\) 取在 \(j \sim r - 1\) 中的 \(h[i]\) 都变成 \(h[i + 1] + 1\)。
最终 \(h\) 数组的最大值就是答案。
为了得到 \(\mathcal O (n)\) 的做法,注意到我们每次是让一个区间的值往左复制了一位,然后加上 \(1\)。
因为是从后往前处理的,不需要管后缀,所以我们可以直接当成是把一个后缀往左复制了一位然后加上 \(1\)。
而且每次往左的那个后缀的位置还都是非严格递减的。
使用一个队列来维护这些往左了的位置,注意到新加入的后缀往左操作会影响到旧的位置,记一个全局标记维护影响,细节见代码。
#include <cstdio>
#include <algorithm>
const int MN = 1000005;
int N, Ans;
char S[MN], T[MN];
int bias, que[MN], head, tail;
int main() {
scanf("%d%s%s", &N, S + 1, T + 1);
int ok = 1;
for (int i = 1; i <= N; ++i) if (S[i] != T[i]) ok = 0;
if (ok) return puts("0"), 0;
head = 1, tail = 0;
for (int i = N, j = N; i >= 1; --i) {
if (j > i) j = i;
while (head <= tail && que[head] + bias > i) ++head;
Ans = std::max(Ans, tail - head + 2);
if (i == 1 || T[i - 1] != T[i]) {
while (j && S[j] != T[i]) --j;
if (!j) return puts("-1"), 0;
--bias;
que[++tail] = j - bias;
--j;
}
}
printf("%d\n", Ans);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号