AtCoder Grand Contest 004
题目传送门:AtCoder Grand Contest 004。
A - Divide a Cuboid
就是平行地切一刀,有偶数就是 \(0\),否则是较小两数乘积。
#include <cstdio>
int main() {
long long A, B, C;
scanf("%lld%lld%lld", &A, &B, &C);
if (~A & 1 || ~B & 1 || ~C & 1) puts("0");
else printf("%lld\n", A > B ? A > C ? B * C : A * B : B > C ? A * C : A * B);
return 0;
}
B - Colorful Slimes
最终考虑某个颜色 \(i\) 的史莱姆,一定是先抓到某个颜色 \(j\) 的史莱姆,然后通过 \((i - j) \bmod N\) 次换颜色操作变成颜色 \(i\) 的。
可以发现所有的变换颜色操作是可以一起做的,也就是说,假设这个 \((i - j) \bmod N\) 的最大值为 \(x\),那就是只要做 \(x\) 次。
枚举 \(x\),然后查询每个颜色以及它往前 \(x\) 个颜色中,抓史莱姆的最小代价即可,时间复杂度为 \(\mathcal O (N^2)\)。
#include <cstdio>
#include <algorithm>
typedef long long LL;
const int MN = 2005;
int N, X, A[MN * 2], B[MN * 2];
LL Ans;
int main() {
scanf("%d%d", &N, &X);
for (int i = 1; i <= N; ++i) {
scanf("%d", &A[i]);
A[N + i] = B[i] = A[i];
Ans += B[i];
}
for (int k = 1; k < N; ++k) {
LL Sum = (LL)k * X;
for (int i = 1; i <= N; ++i) {
B[i] = std::min(B[i], A[N + i - k]);
Sum += B[i];
}
Ans = std::min(Ans, Sum);
}
printf("%lld\n", Ans);
return 0;
}
C - AND Grid
经典构造题,由于边界上不会有紫色的,我们钦定最左边一列全是红色,最右边一列全是蓝色。
然后中间的,有可能有紫色的部分,奇数行全红色,偶数行全蓝色。这样首先保证连通且不重叠。
然后如果哪个地方是紫色的,就在那个地方染上缺少的一种颜色即可。
#include <cstdio>
const int MN = 505;
int N, M;
char A[MN][MN], B[MN][MN], C[MN][MN];
int main() {
scanf("%d%d", &N, &M);
for (int i = 1; i <= N; ++i) {
scanf("%s", A[i] + 1);
for (int j = 1; j <= M; ++j) {
(i & 1 ? B : C)[i][j] = '#';
(i & 1 ? C : B)[i][j] = '.';
}
B[i][1] = C[i][M] = '#';
B[i][M] = C[i][1] = '.';
for (int j = 1; j <= M; ++j)
if (A[i][j] == '#')
B[i][j] = C[i][j] = '#';
}
for (int i = 1; i <= N; ++i) printf("%s\n", B[i] + 1); puts("");
for (int i = 1; i <= N; ++i) printf("%s\n", C[i] + 1);
return 0;
}
D - Teleporter
一开始的形状就是,一个连通的基环内向树,\(1\) 在环里。
最终条件就是,\(a_1 = 1\),然后其它点就形成到 \(1\) 的一棵树,深度不超过 \(K\)(\(1\) 深度为 \(0\))。
那么反正先把 \(a_1\) 给整成 \(1\),然后就是一棵树的结构,然后考虑最深的点如果 \(K\) 步到不了 \(1\) 那就把他的 \(K - 1\) 阶祖先给接到 \(1\) 上。
容易证明这样的贪心是正确的,时间复杂度为 \(\mathcal O (N)\)(如果对深度用基数排序,代码中直接快排)。
#include <cstdio>
#include <algorithm>
#include <vector>
const int MN = 100005;
int N, K, A[MN], Ans;
std::vector<int> G[MN];
int dep[MN], kpar[MN], per[MN], stk[MN], tp;
void DFS(int u) {
stk[++tp] = u;
if (dep[u] > K) kpar[u] = stk[tp - K + 1];
for (int v : G[u]) dep[v] = dep[u] + 1, DFS(v);
--tp;
}
int del[MN];
void Del(int u) {
del[u] = 1;
for (int v : G[u]) if (!del[v]) Del(v);
}
int main() {
scanf("%d%d", &N, &K);
for (int i = 1; i <= N; ++i) scanf("%d", &A[i]);
if (A[1] != 1) A[1] = 1, Ans = 1;
for (int i = 2; i <= N; ++i) G[A[i]].push_back(i);
DFS(1);
for (int i = 1; i <= N; ++i) per[i] = i;
std::sort(per + 1, per + N + 1, [](int i, int j) { return dep[i] > dep[j]; });
for (int i = 1; i <= N; ++i) if (kpar[per[i]] && !del[per[i]]) ++Ans, Del(kpar[per[i]]);
printf("%d\n", Ans);
return 0;
}
E - Salvage Robots
第一步转化:机器人不动,而是出口和边界在动(想象你的手指捏着这个出口 E 在机器人中游走)。
考虑某个时刻,出口在四个方向上的最大移动范围分别为 \(u, d, l, r\)(上下左右),如图:
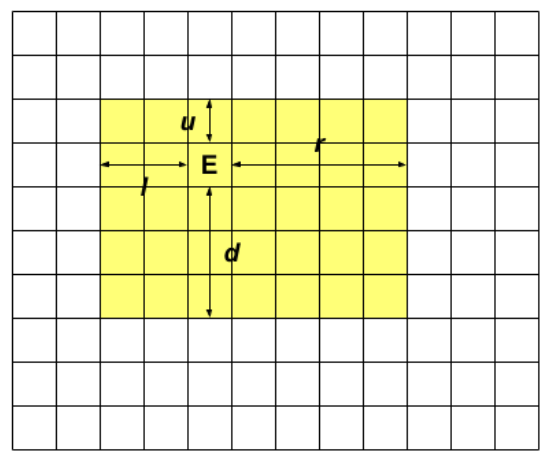
好的,此时黄框内的机器人,只要还没掉下去,那就一定可以被出口吸入(这个词怎么怪怪的)。
但是啥时候才会掉下去呢?我们观察下面这张图的红色部分:
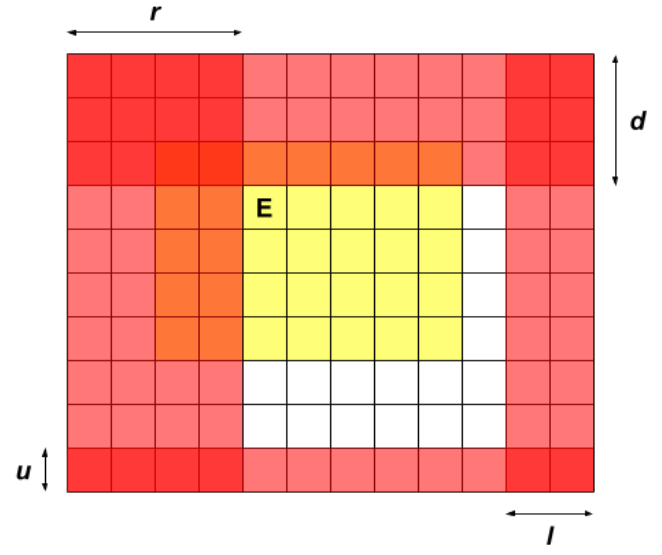
此时红色部分内必然是一个机器人都不留下的,有可能是直接掉下去了,有可能是在掉下去之前被出口给吸走了的,总之已经没了。
那么在这个出口移动的 \(u, d, l, r\) 限制下的最大解救机器人的数量,假设我们已经算出来了,可以发现我们可以做 DP 转移:
记这个数量为 \(\mathrm{f}[u][d][l][r]\),不失一般性,假设下一步出口往下移动,应该转移到 \(\mathrm{f}[u][d + 1][l][r]\)。
在上图中,此时能多被解救的机器人,就是倒数第三行的第五列到第九列内的机器人,也就是在黄色矩形下面的一排白色区域。
如果是出口往右移动,那就是倒数第三列第四行到第七行。如果往上或者往左,那就是一个机器人也救不了——它们全掉下去了。
DP 转移使用前缀和优化一下,最终答案就是黄色矩形变成整个大矩形时的 DP 值,时间复杂度为 \(\mathcal O (N^4)\),数组可以滚动掉一维。
#include <cstdio>
#include <algorithm>
const int MN = 105;
int N, M, px, py, A[MN][MN], B[MN][MN], C[MN][MN];
char s[MN][MN];
int f[MN][MN][MN];
int main() {
scanf("%d%d", &N, &M);
for (int i = 1; i <= N; ++i) {
scanf("%s", s[i] + 1);
for (int j = 1; j <= M; ++j) {
A[i][j] = s[i][j] == 'o';
B[i][j] = B[i][j - 1] + A[i][j];
C[i][j] = C[i - 1][j] + A[i][j];
if (s[i][j] == 'E') px = i, py = j;
}
}
for (int u = 0; u <= px - 1; ++u) {
for (int d = 0; d <= N - px; ++d) {
for (int l = 0; l <= py - 1; ++l) {
for (int r = 0; r <= M - py; ++r) {
int tu = std::max(px - u, 1 + d);
int td = std::min(px + d, N - u);
int tl = std::max(py - l, 1 + r);
int tr = std::min(py + r, M - l);
if (u && px - u == tu && tl <= tr) f[d][l][r] += B[px - u][tr] - B[px - u][tl - 1];
if (d) f[d][l][r] = std::max(f[d][l][r], f[d - 1][l][r] + (px + d == td && tl <= tr ? B[px + d][tr] - B[px + d][tl - 1] : 0));
if (l) f[d][l][r] = std::max(f[d][l][r], f[d][l - 1][r] + (py - l == tl && tu <= td ? C[td][py - l] - C[tu - 1][py - l] : 0));
if (r) f[d][l][r] = std::max(f[d][l][r], f[d][l][r - 1] + (py + r == tr && tu <= td ? C[td][py + r] - C[tu - 1][py + r] : 0));
}
}
}
}
printf("%d\n", f[N - px][py - 1][M - py]);
return 0;
}
F - Namori
当 \(N\) 是奇数时直接输出 \(-1\)。下文默认 \(N\) 为偶数。
原图有三种情况,树,基环树(奇环),基环树(偶环)。需要分类讨论:
当原图为一棵树时:树必然是二分图,我们进行黑白染色。
注意到原本奇怪的条件,在相邻节点颜色不同的情况下,就变成了:把「黑色」移动到相邻节点,更容易理解了。
也就是说:在黑色节点上都放上一枚棋子,我们每次可以把一枚棋子移动到相邻的空节点,最终所有棋子要落到白色节点上。
那么黑白节点数量应该是要相等的,如果相等则一定可行,但是需要的步数是多少呢?
给出结论:考虑每条边,如果这条边的某个方向上原棋子个数为 \(x\),但是目标棋子个数为 \(y\),则显然棋子至少经过该边 \(|x - y|\) 次。
步数即是每条边的这个值的总和,这显然是一个下限。至于为何能取到,限于篇幅不证,感兴趣的直接去看官方题解最后一段就行。
当原图为一棵基环树(奇环)时:我们随意扣掉一条边,此时变成树的情况。注意扣掉的边连接的两点的颜色必然相同。
那么对这条边进行的操作,就相当于在这两个节点上凭空增加或减少一枚棋子。
注意到变成树后,棋子的数量必须要等于白节点的数量,而原棋子数量等于黑节点数量。
而且在扣掉的边上进行的操作,相当于让棋子数 \(+2\) 或 \(-2\)。所以可以直接解出操作的次数(正表示增加,负表示减少)。
然后神奇的一幕出现了,此时那两个节点上可能有不止一枚棋子,甚至可能有负数枚棋子。但是对于树的结论依然成立。
(注意到那个结论甚至没有提到棋子不能重叠之类的问题)
当原图为一棵基环树(偶环)时:我们随意扣掉一条边,此时变成树的情况。注意扣掉的边连接的两点的颜色必然不同。
这个时候仍然是二分图,此时棋子的移动只不过是多了一条边而已。把扣掉的那条边的两端点记作 \(a, b\)。
注意到此时就没法改变棋子的数量了,所以黑白节点数量必须相等。
也没法直接解出被扣掉的边上应该被操作几次了。不过我们可以假设操作了 \(k\) 次(正表示 \(a \to b\) 移动,负则反之)。
操作了 \(k\) 次后,还是变成可能有多枚棋子的情况,照样计算。但是此时我们必须把计算的公式拿出来研究研究了。
可以发现每条边的公式都是 \(|c - d \cdot k|\),其中 \(d\) 的值可能为 \(0\)、\(1\) 或 \(-1\)。
可以发现这只不过就是求一堆 V 字形套了绝对值的一次函数的叠加的最小值。取中位数就好了。
综上所述,三种情况均可以在 \(\mathcal O (N)\) 的时间内完成区分和计算答案(代码中取中位数使用了排序,无伤大雅)。
#include <cstdio>
#include <algorithm>
#include <vector>
typedef long long LL;
const int MN = 100005;
int N, M;
std::vector<int> G[MN];
int a, b, vis[MN], par[MN], dep[MN], num1[MN], num2[MN], kval[MN];
void DFS(int u, int fr) {
vis[u] = 1;
dep[u] = dep[par[u] = fr] + 1;
num1[u] = dep[u] & 1;
num2[u] = ~dep[u] & 1;
for (int v : G[u]) if (v != fr) {
if (!vis[v]) DFS(v, u), num1[u] += num1[v], num2[u] += num2[v];
else a = u, b = v;
}
}
int main() {
scanf("%d%d", &N, &M);
if (N & 1) return puts("-1"), 0;
for (int i = 1; i <= M; ++i) {
int x, y;
scanf("%d%d", &x, &y);
G[x].push_back(y);
G[y].push_back(x);
}
DFS(1, 0);
if (M == N - 1) {
if (num1[1] != num2[1]) return puts("-1"), 0;
LL Ans = 0;
for (int i = 2; i <= N; ++i) {
int x = num2[i] - num1[i];
Ans += x < 0 ? -x : x;
}
printf("%lld\n", Ans);
} else {
if ((dep[a] ^ dep[b]) & 1) {
if (num1[1] != num2[1]) return puts("-1"), 0;
for (int x = a; x; x = par[x]) ++kval[x];
for (int x = b; x; x = par[x]) --kval[x];
LL Ans = 0;
static int seq[MN], cnt;
seq[cnt = 1] = 0;
for (int i = 2; i <= N; ++i) {
if (!kval[i]) {
int x = num2[i] - num1[i];
Ans += x < 0 ? -x : x;
} else
seq[++cnt] = kval[i] * (num2[i] - num1[i]);
}
std::sort(seq + 1, seq + cnt + 1);
int mid = seq[cnt / 2 + 1];
for (int i = 1; i <= cnt; ++i)
Ans += seq[i] < mid ? mid - seq[i] : seq[i] - mid;
printf("%lld\n", Ans);
} else {
int k = N / 2 - num1[1];
for (int x = a; x; x = par[x]) num1[x] += k;
for (int x = b; x; x = par[x]) num1[x] += k;
LL Ans = 0;
for (int i = 2; i <= N; ++i) {
int x = num2[i] - num1[i];
Ans += x < 0 ? -x : x;
}
printf("%lld\n", Ans + (k < 0 ? -k : k));
}
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号