算法复习周------“贪心问题之‘单源最短路径’”

前几天写完了DP问题，终于把比较困难的几个部分写完了，今天开始我们进入贪心模块。贪心相对与DP来说还是很好理解的。NOW，现在开始第一部分。

 

 

算法介绍：给定一个带权有向图，其中的每一条边的权值都是非负数，之后给定一个顶点--“源”，现在要计算从源到所有其他各顶点的最短路径长度（也就是路上各边的权之和）。

 

算法分析：要解决这类问题，我们可以想——我们如何才能使得各边之和最小呢？如果我的每一条边都是最小那么是不是意味着我的总和就是最小？

基于这个思想，我们使用贪心算法。

 

下面看一道例题：

 

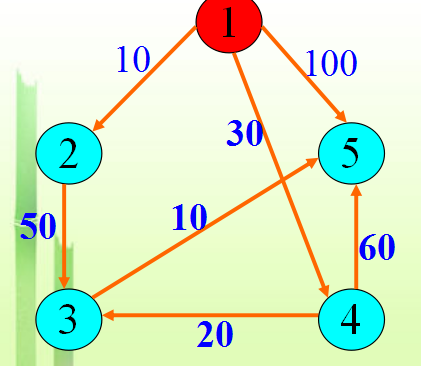
这个图就是我们 的“带权有向图”。我们要求从源---1开始到图中所有其他点的权值之和。这里我们要使用Dijkstra算法。

算法详述：　　在介绍算法之前，我先普及几个基础的知识：

①S代表了当前所处理问题的顶点集合。

②u代表了上一个S+u所得到的集合是当前的S 。 

③dist[i]代表了从“源”到第i个顶点的权值是多少。

 

接下来，我们就一步一步看具体的步骤。——>

①列出当前表格，并写出初始只有源结点的情况

 

根据上面的题目，我们知道当当前我们手中只有“1”这一个点的时候，我们只能够到达2、4、5这三个点，并且在dist[i]中写入权值，又因为1无法直接到3这个店，所以权值为正无穷。

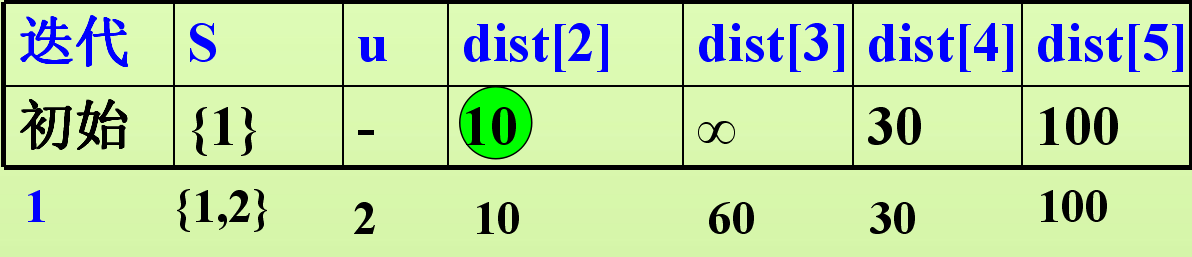
②之后我们选择当前表格中dist[i]最小的那个（这里为10）

 

然后我们的S集合也就从只有1扩展成了｛1，2｝，此时我们再看路程的权值，这个时候我们手里有1，2两个点，那也就意味着我们可以到达3这个点了，并且路径是1->2   +   2->3  =10+50=60。所以更新dist[3]为60。之后又回到刚才的步骤，寻找当前表格中最小的部分（这里大家注意，我们因为已经在上一个表格中处理过dist[2]这个数，所以这里的dist[2]一定是最小值，所以我们在找下一个u的时候不需要考虑dist[2]的值，只需要在30、60、100中找最小的更新下一个S）。

 

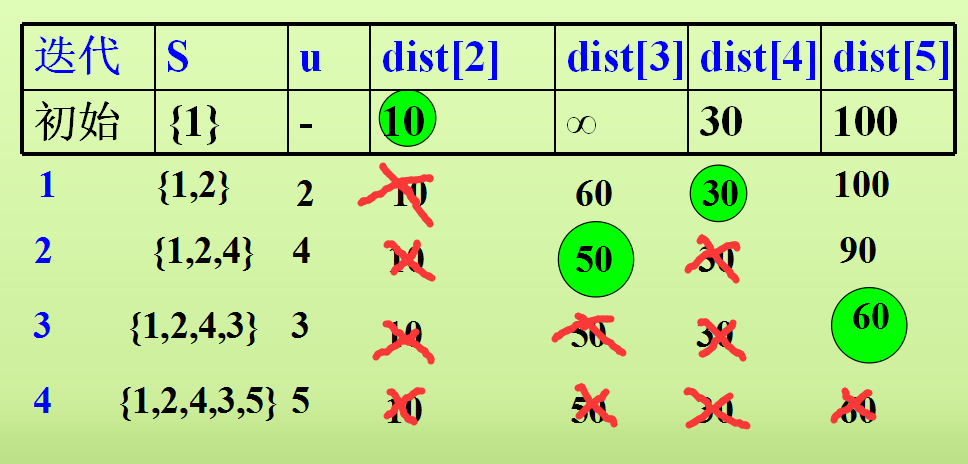
③按照刚才的方法一步一步处理，直到得到下面的表格：

 

PS:这里有一个地方大家要注意，就是我上面提到的只要找到当前集合中路径最小的值之后也就意味着你找到了“源”到顶点i的最短路径。之后的处理就像我下面写的这样，不用写它了，直接从上面移植下来就行。

 

下面给出证明：

 

若A作为源点，与其直接邻接或邻接（所谓的邻接，也就是A→B的路径上或许还存在其它的点）的只有B，C，D三点，其dist[]最小时顶点为C，即A→C为A到C的最短路。但是我们存在疑问的是：是否还存在另一条路径使A到C的距离更小？ 用反证法证明。

假设存在如上图的红色虚线路径，使A→D→C的距离更小，那么A→D作为A→D→C的子路径，其距离也比A→C小，这与前面所述“dist[]最小时顶点为C”矛盾，故假设不成立。因此这个疑问不存在。

也就是说我每次找当前dist[i]中最小的部分就是来解决这个问题的。如果我A到C不是最小（A到D到C权和小的话），那么我就不会说在   选择D进入S之前   把C放到S里（这句话很绕。。。）也就是说A到D肯定小于A到C，我就会把D先放入S中。

 

 

 

 最后我们还有一个问题没有解决，就是最后的写法。在算法中我们列出了一个prev[i]数组，这道题目最后算出来是prev=[1,1,4,1,3]。比如第五个数  代表我5这个结点的上一个结点是3.而3的上一个结点是4，4的上一个是1

倒推回去就是1->4->3->5。就是这样~~~~~~~~~

 

 

啊。。。终于写完了这个，剩下的算法内容也不是很多了~各位加油啊！

 

 

上述内容为算法解析，下面我放入详细的c++代码与解析，方便大家查看。

#include "stack"
#include "iostream"
using namespace std;

int untouched = 99999;
int edge[10][10];
int points;//   点的个数
int edg;//  边的个数
int flag[10];// 标记是否已经处理过此点
int dis[10];//  起始点到任意点的距离
int source,endd;//   起始点与重点
int father[10];//   存放点的串联信息（用来寻找最短路的具体点）

int init(){
    for (int i = 1; i <=points ; ++i) {
        father[i] = 0;//    初始化各个点直接的关系为0----表示还没关系。
        for (int j = 1; j <=points ; ++j) {
            if(i==j) edge[i][j] = 0;//  相等说明自己与自己相连--为0

            else edge[i][j] = untouched;//  不相连说明不可达。所以赋值很大。
        }
    }
}

int main(){
    cin>>points>>edg;
    cin>>source>>endd;// 分别输入点的个数、边的个数、起始点、终止点。
    init();//   进行初始化
    int p1,p2,q;//  分别代表输入的两个点、还有两点之间的权值。
    for (int i = 1; i <=edg ; ++i) {    //初始化各个边的值
        cin>>p1>>p2>>q;
        edge[p1][p2] = q;//  记录两点间的距离
        father[p2] = p1;//   暂时记录p2的父节点为p1。
    }

    for (int j = 1; j <=points ; ++j) {
        dis[j] = edge[source][j];//     dis数组中记录源点到图中任一点的距离。
        flag[j] = 0; //     全标记为false
    }
    flag[source] = 1;// 源点第一个用。
    int minn,u;//   minn为记录当前点所能达到的最短路径的值，u记为最短路的点的具体值。
    for (int k = 1; k <points ; ++k) {  //  不用考虑起始点，所以图中只有n-1个点要扩展。
        minn = untouched;//赋很大的初值。

        for (int i = 1; i <=points ; ++i) {
            if(flag[i]==0 && dis[i] < minn){
                minn = dis[i];
                u = i;//找最短的点，为下一步扩充做准备
            }
        }
        flag[u] = 1;    //将这个点标记

        for (int j = 1; j <=points ; ++j) {
            if(edge[u][j] < untouched && dis[j] > dis[u] + edge[u][j]){//   当u-j之间存在路径并且源点到j的路小于源点经过u到j的路，就更新路径
                dis[j] = dis[u] + edge[u][j];
                father[j] = u;//    更新父节点
            }
        }
    }
    for (int l = 1; l <=points ; ++l) {
        cout<<dis[l]<<" ";
    }

    cout<<endl;
    int tmp;
    stack<int> s;
    s.push(endd);
    //构建堆，用来保存每个节点的父节点信息

    while (source!=endd){
        tmp = father[endd];
        if(tmp == 0) {cout<<"不通路！";
            return 0;}
        s.push(tmp);
        endd = tmp;
    }

    while (!s.empty()){
        cout<<s.top()<<" ";
        s.pop();
    }
}

下面放入上述测试样例：

5 7

1 5

1 2 10

1 5 100

1 4 30

2 3 50

3 5 10

4 3 20

4 5 60

 

 

得到结果：

0 10 50 30 60
1 4 3 5

第一行为源点到各个点的路径长度

第二行为source到endd的最优路径

 

————————————————————————————Made By  Pinging