C++ 数据结构 2:栈和队列
1 栈
1.1 栈的基本概念
栈(stack)又名堆栈,它是一种 运算受限的线性表。限定 仅在表尾进行插入和删除操作 的线性表。表尾被称为栈顶,相对地,把另一端称为栈底。
1.1.1 特点
它的特殊之处在于限制了这个线性表的插入和删除的位置,它始终只在栈顶进行。这也就使得:栈底是固定的,最先进栈的只能在栈底。
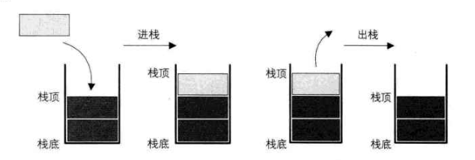
1.2 栈的常用操作
-
创建栈
-
销毁栈
-
清空栈
-
进栈
-
出栈
-
获取栈顶元素
-
获取栈的大小
1.2.1 栈的抽象数据类型
ADT 栈(stack)
Data
通线性表。元素具有相同的类型,相邻的元素具有前驱和后继关系。
Operation
// 初始化,建立一个空栈S
InitStack(*S);
// 若栈存在,则销毁它
DestroyStack(*S);
// 将栈清空
ClearStack(*S);
// 若栈为空则返回true,否则返回false
StackEmpty(S);
// 若栈存在且非空,用e返回S的栈顶元素
GetTop(S,*e);
// 若栈S存在,插入新元素e到栈S中并成为其栈顶元素
Push(*S,e);
// 删除栈S中的栈顶元素,并用e返回其值
Pop(*S, *e);
// 返回栈S的元素个数
StackLength(S);
endADT
1.3 栈的顺序存储
1.3.1 基本概念
基本概念:
栈的顺序存储结构简称顺序栈,它是运算受限制的顺序表。顺序栈的存储结构是:利用一组地址连续的的存储单元依次存放自栈底到栈顶的数据元素,同时附设指针top只是栈顶元素在顺序表中的位置。
栈是先进后出的线性表。
1.3.2 设计与实现
因为栈是一种特殊的线性表,所以栈的顺序存储可以通过顺序线性表来实现。
示例代码:

SqStack.h
#ifndef _SQSTACK_H
#define _SQSTACK_H
#define MAXSIZE 50
typedef int EnumType;
typedef struct _SQSTACK
{
int top; // 栈顶指针
EnumType data[MAXSIZE];
}SqStack;
// 初始化,建立一个空栈S
void InitStack(SqStack *S);
// 将栈清空
void ClearStack(SqStack *S);
// 若栈为空则返回true,否则返回false
int StackEmpty(SqStack S);
// 若栈存在且非空,用e返回S的栈顶元素
void GetTop(SqStack S, EnumType *e);
// 若栈S存在,插入新元素e到栈S中并成为其栈顶元素
void Push(SqStack *S, EnumType e);
// 删除栈S中的栈顶元素,并用e返回其值
void Pop(SqStack *S, EnumType *e);
// 返回栈S的元素个数
int StackLength(SqStack S);
#endif // _SQSTACK_H
SqStack.c
#include "SqStack.h"
#include <string.h>
void InitStack(SqStack *S)
{
// 空栈
S->top = -1;
memset(S->data, 0, sizeof(S->data));
}
void ClearStack(SqStack *S)
{
S->top = -1;
}
int StackEmpty(SqStack S)
{
if (S.top == -1)
{
return 1;
}
return 0;
}
void GetTop(SqStack S, EnumType *e)
{
// 栈为空
if (S.top == -1 && S.data[S.top]!= 0)
{
return;
}
*e = S.data[S.top];
}
void Push(SqStack *S, EnumType e)
{
// 栈已经满了
if (S->top == MAXSIZE - 1)
{
return;
}
// 栈顶上移
S->top++;
// 赋值
S->data[S->top] = e;
}
void Pop(SqStack *S, EnumType *e)
{
// 栈为空
if (S->top == -1 && S->data[S->top]!= 0)
{
return;
}
// 赋值
*e = S->data[S->top];
// 栈顶指针下移
S->top--;
}
int StackLength(SqStack S)
{
return S.top + 1;
}
main.c
#include "SqStack.h"
#include <stdio.h>
#include <stdlib.h>
void main()
{
// 定义栈变量
SqStack st;
int i = -1;
// 初始化栈
InitStack(&st);
// 压栈
for (i = 0; i < 10; ++i)
{
Push(&st,i+1);
}
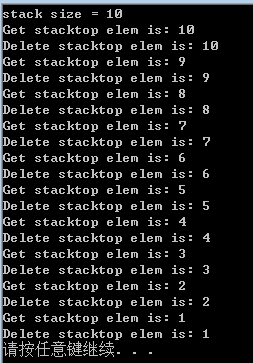
printf("stack size = %d\n", StackLength(st));
// 出栈
while (StackEmpty(st) != 1)
{
int temp;
// 取栈顶元素
GetTop(st, &temp);
printf("Get stacktop elem is: %d\n", temp);
// 删除栈顶元素
Pop(&st, &temp);
printf("Delete stacktop elem is: %d\n", temp);
}
system("pause");
}
运行结果:
1.4 栈的链序存储
1.4.1 基本概念
栈的链式存储结构简称链栈。
1.4.2 设计与实现
链栈是一种特殊的线性表,链栈可以通过链式线性表来实现。
示例代码:
LinkStack.h
#ifndef _LINKSTACK_H
#define _LINKSTACK_H
// 定义小链表节点
typedef struct NODE
{
struct NODE* next;
}Node;
// 链表结构体
typedef struct
{
// 栈顶指针
Node *top;
// 长度
int length;
}LinkStack;
// 初始化,建立一个空栈S
void InitStack(LinkStack *S);
// 将栈清空
void ClearStack(LinkStack *S);
// 若栈为空则返回true,否则返回false
int StackEmpty(LinkStack S);
// 若栈存在且非空,用e返回S的栈顶元素
void GetTop(LinkStack S, Node **e);
// 若栈S存在,插入新元素e到栈S中并成为其栈顶元素
void Push(LinkStack *S, Node *e);
// 删除栈S中的栈顶元素,并用e返回其值
void Pop(LinkStack *S, Node **e);
// 返回栈S的元素个数
int StackLength(LinkStack S);
#endif // _LINKSTACK_H
LinkStack.c
#include "LinkStack.h"
#include <stdio.h>
void InitStack(LinkStack *S)
{
S->length = 0;
S->top = NULL;
}
void ClearStack(LinkStack *S)
{
while (S->length)
{
Node* p;
Pop(S, &p);
}
}
int StackEmpty(LinkStack S)
{
if (S.length == 0)
{
return 1;
}
return 0;
}
void GetTop(LinkStack S, Node **e)
{
// 空栈
if (S.length == 0 || S.top == NULL)
{
return;
}
*e = S.top;
}
// 栈顶是链表头部
void Push(LinkStack *S, Node *e)
{
// 节点e插入到链表的头部
e->next = S->top;
// top指针指向第一个节点
S->top = e;
// 长度+1
S->length++;
}
void Pop(LinkStack *S, Node **e)
{
// 删除第一个节点
Node* pDel = S->top;
// 空栈
if (S->length == 0)
{
return;
}
// 赋值
*e = pDel;
// 栈顶指针后移
S->top = pDel->next;
// 长度减1
S->length--;
}
int StackLength(LinkStack S)
{
return S.length;
}
main.c
#include <stdio.h>
#include <stdlib.h>
#include "LinkStack.h"
// 业务节点
typedef struct stu
{
// 包含链表节点
Node node;
int id;
int age;
}Student;
void main()
{
Student stu[10];
// 链表结构变量
LinkStack st;
int i = -1;
// 初始化栈
InitStack(&st);
// 初始化数组
for (i = 0; i < sizeof(stu) / sizeof(Student); ++i)
{
stu[i].id = i;
stu[i].age = i + 20;
// 数据添加链表中
Push(&st, &stu[i].node);
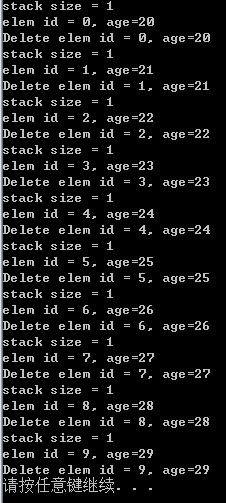
printf("stack size = %d\n", StackLength(st));
while (StackEmpty(st) != 1)
{
Node* p = NULL;
Student* pp = NULL;
// 获取栈顶元素
GetTop(st, &p);
pp = (Student*)p;
printf("elem id = %d, age=%d\n", pp->id, pp->age);
// 删除
Pop(&st, &p);
pp = (Student*)p;
printf("Delete elem id = %d, age=%d\n", pp->id, pp->age);
}
}
system("pause");
}
运行结果:
2 队列
2.1 基本概念
队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头。

2.1.1 特点
队列是先进先出的线性表。
在队尾添加元素,在队头删除元素。
判断队列是空队列还是已满呢?
-
栈空: 队首标志 = 队尾标志时,表示栈空。
-
栈满 : 队尾 + 1 = 队首时,表示栈满。
2.2 队列的常用操作
-
创建队列
-
销毁队列
-
清空队列
-
进队列
-
出队列
-
获取队头元素
-
获取队列的长度
2.2.1 队列的抽象数据类型
ADT 队列(Queue)
Data
通线性表。元素具有相同的类型,相邻元素具有前驱后继关系。
Operation
// 初始化操作,建立一个空队列Q
InitQueue(*Q);
// 若队列Q存储,则销毁它。
DestroyQueue(*Q);
// 将队列Q清空
ClearQueue(*Q);
// 若队列为空则返回true,否则返回false
QueueEmpty(Q);
// 若队列Q存在且非空,用e返回队列Q的队头元素
GetHead(Q, *e);
// 若队列Q存在,插入新元素e到队列Q中并成为队尾元素。
EnQueue(*Q, e);
// 删除队列Q中的队头元素,并用e返回其值
DeQueue(*Q, *e);
// 返回队列Q的元素个数
QueueLength(Q);
endADT
2.3 队列顺序模型和链表模型关系分析
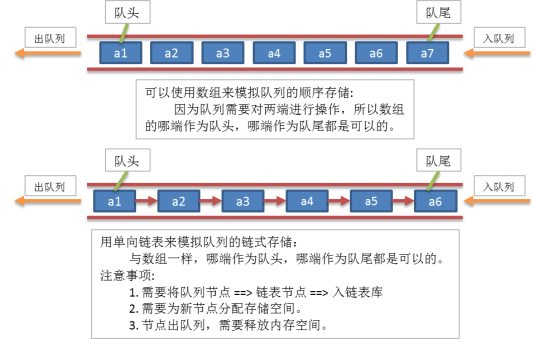
2.4 队列的顺序存储
2.4.1 基本概念
队列也是一种特殊的线性表;可以用线性表顺序存储来模拟队列。
2.4.2 设计与实现
示例代码:
SqQueue.h
#ifndef _SQQUEUE_H
#define _SQQUEUE_H
#define MAXSIZE 50
typedef int EnumType;
typedef struct _SQQUEUE
{
// 尾节点指针
int rear;
// 头结点指针
int front;
EnumType data[MAXSIZE];
}SqQueue;
// 初始化操作,建立一个空队列Q
void InitQueue(SqQueue *Q);
// 将队列Q清空
void ClearQueue(SqQueue *Q);
// 若队列为空则返回true,否则返回false
int QueueEmpty(SqQueue Q);
// 若队列Q存在且非空,用e返回队列Q的队头元素
void GetHead(SqQueue Q, EnumType* e);
// 若队列Q存在,插入新元素e到队列Q中并成为队尾元素。
void EnQueue(SqQueue *Q, EnumType e);
// 删除队列Q中的队头元素,并用e返回其值
void DeQueue(SqQueue *Q, EnumType* e);
// 返回队列Q的元素个数
int QueueLength(SqQueue Q);
#endif //_SQQUEUE_H
SqQueue.c
#include "SqQueue.h"
#include <string.h>
void InitQueue(SqQueue *Q)
{
Q->rear = Q->front = 0;
memset(Q->data, 0, sizeof(Q->data));
}
void ClearQueue(SqQueue *Q)
{
Q->rear = Q->front = 0;
memset(Q->data, 0, sizeof(Q->data));
}
int QueueEmpty(SqQueue Q)
{
if (Q.rear == Q.front)
{
return 1;
}
return 0;
}
// 返回队首元素的值,但不删除该元素
void GetHead(SqQueue Q, EnumType* e)
{
// 队列为空
if (Q.rear == Q.front)
{
return;
}
*e = Q.data[Q.front];
}
// 在队尾压入新元素
void EnQueue(SqQueue *Q, EnumType e)
{
// 队列已经满了
if (Q->rear -1 == MAXSIZE)
{
return;
}
else
{
// 赋值
Q->data[Q->rear] = e;
// 队尾上移
Q->rear++;
}
}
// 删除队列首元素
void DeQueue(SqQueue *Q, EnumType* e)
{
// 队列为空
if (Q->rear == Q->front)
{
return;
}
// 赋值
*e = Q->data[Q->front];
// front指针上移
Q->front++;
}
int QueueLength(SqQueue Q)
{
return Q.rear;
}
main.c
#include "SqQueue.h"
#include <stdio.h>
#include <stdlib.h>
void main()
{
// 队列变量
SqQueue q;
int i = -1;
// 初始化队列
InitQueue(&q);
// 入队列
for (i = 0; i < 5; ++i)
{
EnQueue(&q, i+1);
}
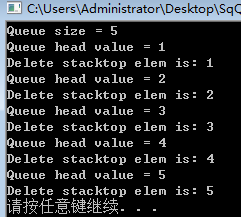
printf("Queue size = %d\n", QueueLength(q));
// 删除全部节点
while (QueueEmpty(q) != 1)
{
int temp;
// 取栈顶元素
GetHead(q, &temp);
printf("Queue head value = %d\n",temp);
// 删除栈顶元素
DeQueue(&q, &temp);
printf("Delete stacktop elem is: %d\n", temp);
}
system("pause");
}
运行结果:
2.5 队列的链序存储设计与实现
2.5.1 基本概念
队列也是一种特殊的线性表;可以用线性表链式存储来模拟队列的链式存储。
2.5.2 设计与实现
示例代码:
LinkQueue.h
#ifndef _LINKQUEUE_H
#define _LINKQUEUE_H
typedef struct _NODE
{
struct _NODE* next;
}Node;
typedef struct
{
// 长度
int length;
// 尾节点指针
Node *rear;
// 头结点指针
Node *front;
}LinkQueue;
// 初始化操作,建立一个空队列Q
void InitQueue(LinkQueue *Q);
// 将队列Q清空
void ClearQueue(LinkQueue *Q);
// 若队列为空则返回true,否则返回false
int QueueEmpty(LinkQueue Q);
// 若队列Q存在且非空,用e返回队列Q的队头元素
void GetHead(LinkQueue Q, Node** e);
// 若队列Q存在,插入新元素e到队列Q中并成为队尾元素。
void EnQueue(LinkQueue *Q, Node* e);
// 删除队列Q中的队头元素,并用e返回其值
void DeQueue(LinkQueue *Q, Node** e);
// 返回队列Q的元素个数
int QueueLength(LinkQueue Q);
#endif //_LINKQUEUE_H
LinkQueue.c
#include "LinkQueue.h"
#include <stdio.h>
void InitQueue(LinkQueue *Q)
{
Q->length = 0;
Q->rear = NULL;
Q->front = NULL;
}
void ClearQueue(LinkQueue *Q)
{
while (Q->length)
{
Node* p;
DeQueue(Q, &p);
}
}
int QueueEmpty(LinkQueue Q)
{
if (Q.length == 0)
{
return 1;
}
return 0;
}
// 链表的头部为队头, 尾部为队尾
void GetHead(LinkQueue Q, Node** e)
{
// 错误处理
if (Q.length == 0)
{
return;
}
*e = Q.front;
}
void EnQueue(LinkQueue *Q, Node* e)
{
if (Q->length == 0)
{
// 空链表
Q->rear = Q->front = e;
}
else
{
// 新节点放到队尾
Q->rear->next = e;
// rear指向最后一个节点
Q->rear = e;
}
// 长度
Q->length++;
}
void DeQueue(LinkQueue *Q, Node** e)
{
if (Q->length == 0)
{
// 空链表
return;
}
// 赋值
*e = Q->front;
// front指针后移
Q->front = Q->front->next;
// 长度
Q->length--;
if (Q->length == 0)
{
// 删除最后一个节点的时候, 尾指针需要指向NULL
Q->rear = NULL;
}
}
int QueueLength(LinkQueue Q)
{
return Q.length;
}
main.c
#include "LinkQueue.h"
#include <stdio.h>
#include <stdlib.h>
void main()
{
// 业务节点
typedef struct _tag_value
{
// 包含一个链表节点
Node node;
// 数据
int v;
}Value;
Value val[5];
// 队列变量
LinkQueue q;
int i = -1;
// init
InitQueue(&q);
for (i = 0; i < 5; ++i)
{
val[i].v = i + 20;
// 入队列
EnQueue(&q, &val[i].node);
}
printf("Queue size = %d\n", QueueLength(q));
// 删除全部节点
while (QueueEmpty(q) != 1)
{
// 取出队头元素
Node* p;
Value* pp;
GetHead(q, &p);
pp = (Value*)p;
printf("Queue head value = %d\n", pp->v);
// 出队列
DeQueue(&q, &p);
pp = (Value*)p;
printf("Delete Queue head value = %d\n", pp->v);
}
system("pause");
}
运行结果:


