复杂度估计

时间复杂度

假设OJ上设定运行时间超过1s便报超时，那么

1s 运行O(n),O(n^2),O(logn)的算法分别可以有多少次？

查看CPU参数（一般PC就是在2~3GHz这样）

• 1GHz（兆赫）= 1000MHz（兆赫）
• 1MHz（兆赫）= 1百万赫兹

 1GHz = 10亿Hz，表示CPU可以一秒脉冲10亿次（有10亿个）

 word cpu 2.90GHz，也就是说晶振每秒发出30亿次脉冲（时钟周期）

实现三个函数，时间复杂度分别是 $O(n)$ , $O(n^2)$, $O(n\log n)$，使用加法运算来测试一下。

#include <iostream>
#include <chrono>
#include <thread>
using namespace std;
using namespace chrono;
// O(n)
void function1(long long n) {
    long long k = 0;
    for (long long i = 0; i < n; i++) {
        k++;
    }
}

// O(n^2)
void function2(long long n) {
    long long k = 0;
    for (long long i = 0; i < n; i++) {
        for (long j = 0; j < n; j++) {
            k++;
        }
    }

}
// O(nlogn)
void function3(long long n) {
    long long k = 0;
    for (long long i = 0; i < n; i++) {
        for (long long j = 1; j < n; j = j * 2) { // 注意这里j=1
            k++;
        }
    }
}
int main() {
    long long n; // 数据规模
    while (1) {
        cout << "输入n：";
        cin >> n;
        milliseconds start_time = duration_cast<milliseconds>(
            system_clock::now().time_since_epoch()
            );
        //function1(n);//600000000
        //function2(n);//30000
        function3(n);//30000000
        milliseconds end_time = duration_cast<milliseconds>(
            system_clock::now().time_since_epoch()
            );
        cout << "耗时:" << milliseconds(end_time).count() - milliseconds(start_time).count()
            << " ms" << endl;
    }
}

测试后，在我的机器上1s中能运行复杂度分别为O(n),O(n^2),O(logn)的算法次数大概：

O(n) ：600000000

O(n^2) ：30000

O(logn) ：30000000

递归算法的时间复杂度

递归算法的时间复杂度本质上是要看: 递归的次数 * 每次递归中的操作次数。

用求x^n来说明什么是O(logn)的复杂度的算法，和O(n)复杂度算法的区别。

求x^n

直接一个for循环

int function1(int x, int n) {
    int result = 1;  // 注意 任何数的0次方等于1
    for (int i = 0; i < n; i++) {
        result = result * x;
    }
    return result;
}

时间复杂度：O(n)

怎么才O(n)？隔壁老王都会写O(logn)了

提示：使用递归降低复杂度

反手就是一个递归

int function2(int x, int n) {
    if (n == 0) {
        return 1; // return 1 同样是因为0次方是等于1的
    }
    return function2(x, n - 1) * x;
}

背公式：递归的次数 * 每次递归中的操作次数； n * 1 = n

时间复杂度：O(n)

怎么才O(n)？隔壁老王都会写O(logn)了，能不能给点力？

改一改递归

int function3(int x, int n) {
    if (n == 0) {
        return 1;
    }
    if (n % 2 == 1) {
        return function3(x, n / 2) * function3(x, n / 2)*x;
    }
    return function3(x, n / 2) * function3(x, n / 2);
}

背公式：递归的次数 * 每次递归中的操作次数；

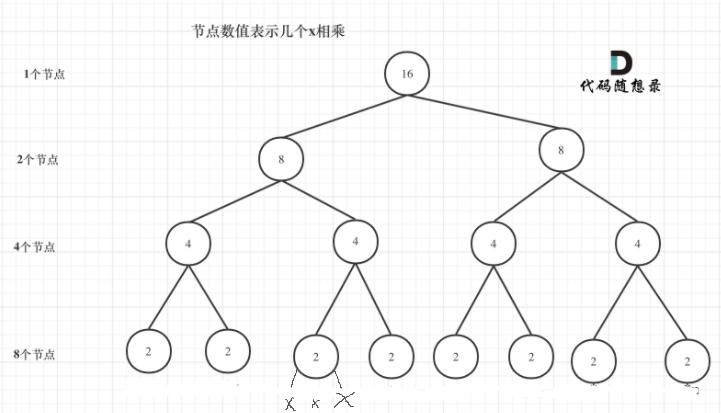
算法看成是一颗满二叉树，每个节点算一次 乘法操作，有多少个节点？$2^m+2^{m-1}+\ldots+2^0$ = 2^{m+1} - 1 , m = \log_{2}{n} - 1$ m为递归深度

时间复杂度：O(2^(log_2^n ) ) = O(n)

怎么才O(n)？隔壁老王O(logn)都写了好几个了，你行不行？

上面的算法，显然有重复计算，function3(x, n / 2) * function3(x, n / 2) ，* 两边就做了一样的事情。

---

 

递归有时候的时间复杂度可以很烂甚至是指数复杂度算法

比如说下面这个求斐波那契的算法，老王反手就丢出一个递归

int fibonacci(int i) {
       if(i <= 0) return 0;
       if(i == 1) return 1;
       return fibonacci(i-1) + fibonacci(i-2);
}

小张：哇大佬会递归，好厉害！

Carl：笑死，这都$O(2^n)$算法了，n一大，凉凉！

小张一脸懵逼~：这怎么会是$O(2^n)$算法，你说说，是的话我吃掉

背公式：递归的次数 * 每次递归的时间复杂度

每次递归都是$O(1)$的操作，那看递归了多少次，将i为5作为输入的递归过程 抽象成一颗递归树，如图：

 

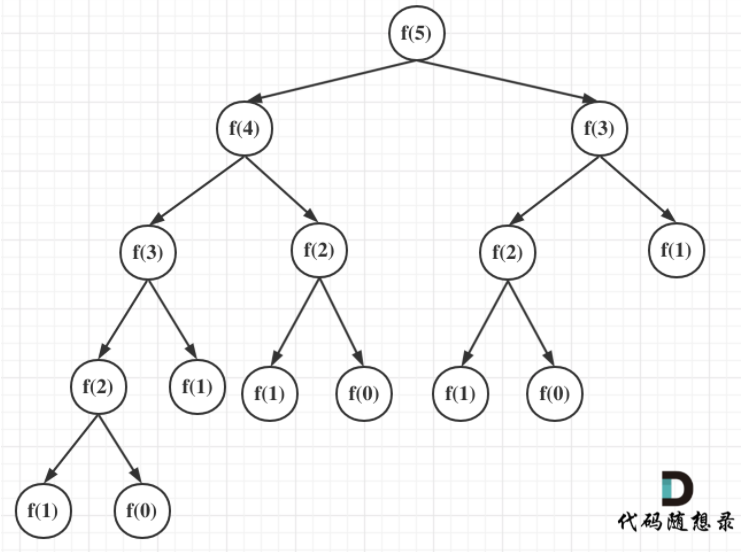
 一棵深度为n的二叉树最多可以有 2^n - 1 个节点。所以算法的时间复杂度为$O(2^n)$

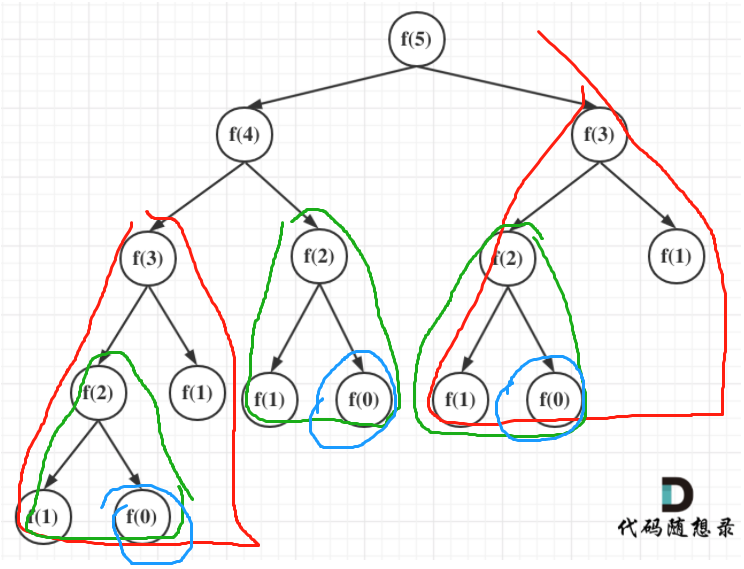
这种求斐波那契数的算法看似简洁，其实时间复杂度非常高，一般不推荐这样来实现斐波那契。

主要是两次递归有大量重复计算，导致时间复杂度指数上升

return fibonacci(i-1) + fibonacci(i-2);

 

 老王：我只是试试你而已，我当然会O(n)算法

int fibonacci(int first, int second, int n) {
    if (n <= 0) {
        return 0;
    }
    if (n < 3) {
        return 1;
    }
    else if (n == 3) {
        return first + second;
    }
    else {
        return fibonacci(second, first + second, n - 1);
    }
}

这里相当于用first和second来记录当前相加的两个数值，此时就不用两次递归了。

因为每次递归的时候n减1，即只是递归了n次，所以时间复杂度是 $O(n)$。

同理递归的深度依然是n，每次递归所需的空间也是常数，所以空间复杂度依然是$O(n)$。

---

 

 

$O(\log n)$，行！

int function4(int x, int n) {
    if (n == 0) {
        return 1;
    }
    int t = function4(x, n / 2);// 这里相对于function3，是把这个递归操作抽取出来
    if (n % 2 == 1) {
        return t * t * x;
    }
    return t * t;
}

依然还是看递归了多少次，可以看到这里仅仅有一个递归调用，且每次都是n/2 ，所以这里我们一共调用了 $\log_{2}{n}$ 次function4。

每次递归了做都是一次乘法操作，这也是一个常数项的操作，那么这个递归算法的时间复杂度才是真正的$O(\log n)$。

空间复杂度

主要目的，还是对程序要使用多大内存有个估计，不至于 out of memory ...

栗子

空间复杂度是$O(1)$

int j = 0;
for (int i = 0; i < n; i++) {
    j++;
}

所需的内存空间并不会随着n的变化而变化。即此算法空间复杂度为一个常量，所以表示为大$O(1)$

空间复杂度是$O(n)$

int* a = new int(n);
for (int i = 0; i < n; i++) {
    a[i] = i;
}

delete a;

可以看出消耗空间和输入参数n保持线性增长，n多大就开辟多大的空间。

$O(n^2)$， $O(n^3)$， $O(2^n)$如是，最好不要是指数算法。

递归算法空间复杂度

在递归的时候，可能会出现空间复杂度为logn的情况。

那么递归算法的空间复杂度怎么估计呢？

公式：递归算法的空间复杂度 = 每次递归的空间复杂度 * 递归深度

为什么要求递归的深度呢？

因为每次递归所需的空间都被压到调用栈里（这是内存管理里面的数据结构，和算法里的栈原理是一样的），一次递归结束，这个栈就是就是把本次递归的数据弹出去。所以这个栈最大的长度就是递归的深度。

每次递归的空间复杂度，即每次递归需要的栈空间

还是用老王写的斐波那契来说明

非递归dp版本，时间复杂度$O(n)$空间复杂度$O(1)$

int fib(int n) {
    //https://leetcode-cn.com/problems/fei-bo-na-qi-shu-lie-lcof
    //计算Fibonacci的第n项值  如果初始结果大于1e9+7 即1000000007要取模
    //题解  可以用递归  但是有大量重复运算   
    /*
    //递归  当n太大时，超出时间限制
     if(n <= 1 || n > 100){
        return n;
    }
    return (fib(n-1) + fib(n-2))%1000000007;
    */

    //动态规划 O（N）  O(1)
    if (n <= 1 || n > 100) {
        return n;
    }
    int leftleft = 0;
    int left = 1;
    int num = 0;
    for (int i = 0; i < n - 1; i++) {
        num = (left + leftleft) % 1000000007;
        leftleft = left;
        left = num;
    }
    return num;

}

递归算法，时间复杂度$O(2^n)$空间复杂度$O(n)$

int fibonacci(int i) {
       if(i <= 0) return 0;
       if(i == 1) return 1;
       return fibonacci(i-1) + fibonacci(i-2);
}

优化递归算法时间复杂度$O(n)$空间复杂度$O(n)$

int fibonacci(int first, int second, int n) {
    if (n <= 0) {
        return 0;
    }
    if (n < 3) {
        return 1;
    }
    else if (n == 3) {
        return first + second;
    }
    else {
        return fibonacci(second, first + second, n - 1);
    }
}

求斐波那契数的时候，使用递归算法并不一定是在性能上是最优的，但递归确实简化的代码层面的复杂度。

二分查找递归算法

二分查找的递归实现

int binary_search( int arr[], int l, int r, int x) {
    if (r >= l) {
        int mid = l + (r - l) / 2;
        if (arr[mid] == x)
            return mid;
        if (arr[mid] > x)
            return binary_search(arr, l, mid - 1, x);
        return binary_search(arr, mid + 1, r, x);
    }
    return -1;
}

时间复杂度$O(\log n)$, 空间复杂度$O(\log n)$

二分查找的时间复杂度是$O(\log n)$，那么递归二分查找的空间复杂度是多少呢？

背公式：每次递归的空间复杂度 * 递归深度

每次递归的空间复杂度 ：C++中传入arr是一个地址并不是拷贝，所以每次递归的空间复杂度是常数即：$O(1)$

递归深度：二分查找的递归深度是logn

总的空间复杂度为$O(\logn)$

注意，比如说用python时，转入的参数是整个拷贝，那么再用上面的二分查找空间复杂度就是$O(n\logn)$了。

但是呢，算法的空间复杂度不一定是整个程序跑起来的实际内存消耗，只能说可以用来粗略地估计。

代码的内存消耗

请看Carl哥的讲代码的内存消耗：代码随想录 (programmercarl.com)

为什么要内存对齐？

CPU读取内存不是一次读取单个字节，而是一块一块的来读取内存，块的大小可以是2，4，8，16个字节，具体取多少个字节取决于硬件。

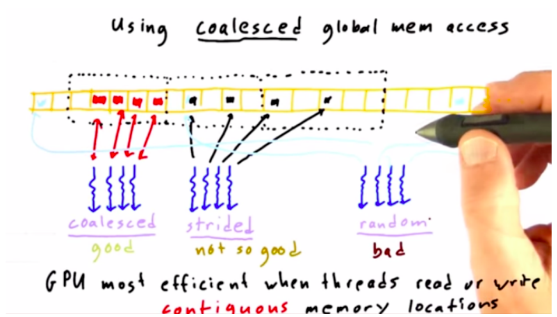
就像GPU中，提高GPU的运行速度的策略之一就是合并对全局内存的访问。

GPU中，读取全局内存时，是一块一块读取的，尽管只希望读取一个地址的元素。如果线程读取或者写入连续的全局内存位置，GPU的效率是最高的，这就叫做 coalesced 合并，是好的。有时候读取的不是连续的一块内存，可能有间隔，那就叫做 strided 跨步，不是很好的。更糟糕的是，如果随机从一个位置读取，那么就需要非常多次内存操作，这就导致 GPU 性能差。

 

有同学会问了，那这样岂不是会消耗内存资源，当然会，但是我们更希望的是速度速度！天下武功，为快不破🐱‍💻