捷联惯导和组合导航学习笔记

捷联惯导和组合导航学习笔记

坐标系定义与符号约定

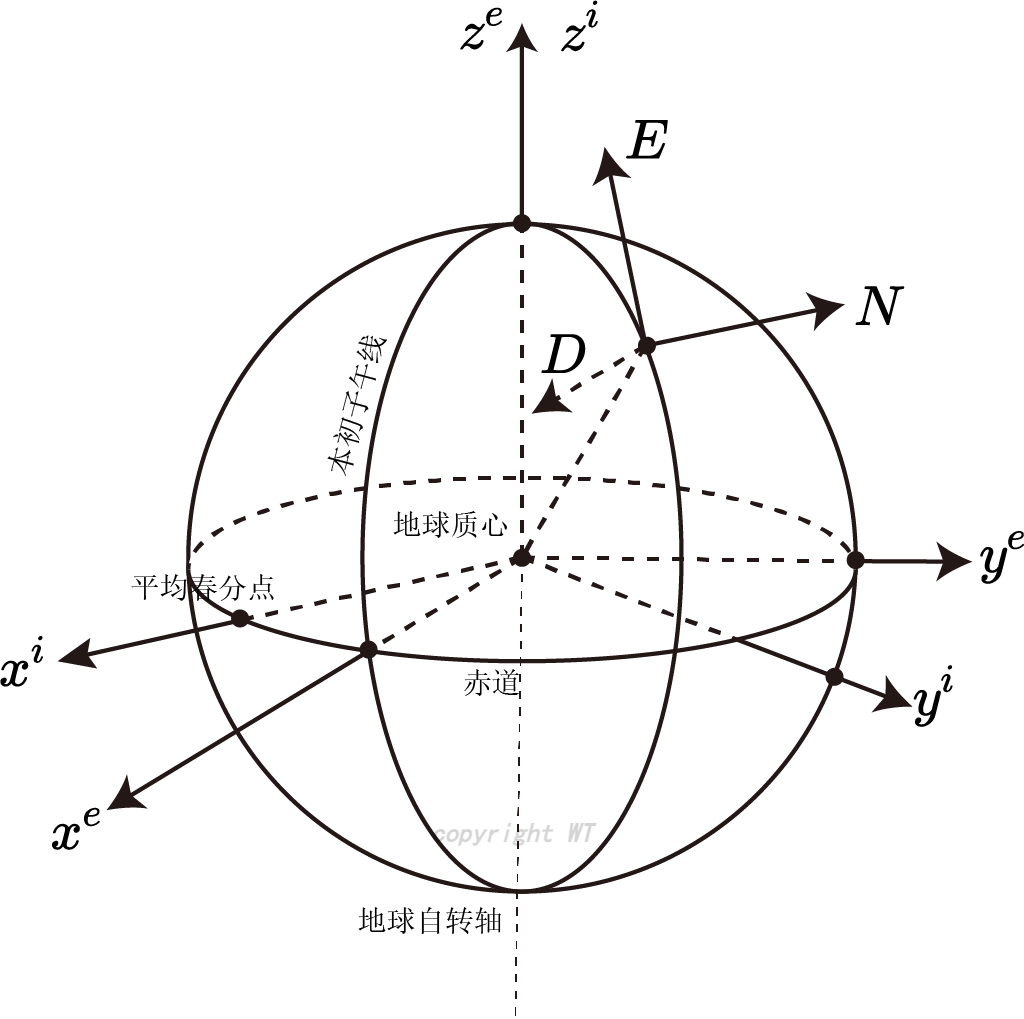
惯性坐标系（\(i\)系）

\(O-x_iy_iz_i\) ，取地球中心为坐标原点，\(ox\)轴是地球围绕太阳公转平面的黄道平面和地球赤道平面的交线，\(oy\)轴用右手规则确定，\(oz\)轴沿着地球自转轴方向。地心坐标系与地球不固连，不随地球转动，惯性期间测得的物理量是相对于惯性坐标系的。

地球坐标系（\(e\)系）

\(O-x_ey_ez_e\)，地球中心为原点，\(oz\)轴沿着地球自转轴方向，\(ox\)是赤道平面与本初子午面交线，\(oy\)轴沿用右手规则。也叫地心地固坐标系。地心地固坐标系和地球固连，与地球一起相对惯性坐标系以地球的自转角速度进行转动。

地理坐标系（\(g\)系）

\(O-x_gy_gz_g\)，地理坐标系也叫做站心坐标系，常用的是“东北天”，“北东地”坐标系，一般描述横滚角、俯仰角和航向角，都是定义在\(g\)系。

载体坐标系（\(b\)系）

\(O-x_gy_gz_g\)，载体坐标系与载体固连，原点在载体中心，一般遵循“右前上”的准则。

传感器坐标系

在不考虑安装偏角的情况下，一般与载体坐标系重合。、

导航坐标系（\(n\)系）

导航坐标系是惯性导航算法的基本参考系，运动物体在导航坐标系内进行位置、速度、姿态确定，可选取e系或g系做为导航系。在e系内导航，可以直接确定地心地固系下的导航参数，便于和GNSS 等大地测量手段相结合，在惯性导航中，经常将地理坐标系g作为导航坐标系。值得注意的是，导航坐标系只是一个“虚”的概念。

WGS84坐标系

wgs84表示的就是地理经纬度，也叫经纬高坐标系(经度(longitude)，纬度(latitude)和高度(altitude)LLA坐标系)。

符号约定

\(w_{ib}\)，\(b\)系相对于\(i\)系的转动。

\(C^n_b\) ，表示从\(b\)系到\(n\)系的变换矩阵。

四元数微分方程与求解

关于四元数的基础知识在这里不赘述，相关书籍和资料都有，这里主要记录自己遇到的一些问题。

四元数的微分方程为：

\[\dot{q}=\frac{1}{2}Wq \]

其中

\[W=\begin{bmatrix} 0& -\omega_x& -\omega_y& -\omega_z\\ \omega_x& 0& \omega_z& \omega_y\\ \omega_y& -\omega_z& 0& \omega_x\\ \omega_z& \omega_y& -\omega_z&0 \end{bmatrix} \]

求解微分方程的方法有很多，这里主要使用的龙格库塔法，有一阶龙格库塔法和四阶龙格库塔法，在工程上应用广泛的高精度单步算法，其中包括著名的欧拉法，用于数值求解微分方程。

由一阶龙格库塔法\(y_{n+1}=y_n+h\cdot y'\) ，可以得到四元数微分方程的解：

\[Q[t+\Delta t ]=Q[t]+\Delta t\frac{dQ}{dt} \]

\[\because \frac{dQ}{dt} =\frac{1}{2}Wq \]

\[\therefore Q[t+\Delta t ]=\frac{1}{2} \Delta t[I+W]q \]

这里定义\(R=I+W\)为状态转移矩阵。