组合数学选讲
前言:或许是讲的最详细的一次吧
前置姿势
一大堆呀,挑主要的整理一些
- 基本概念,若\(a\times b \equiv 1\pmod p\) 则称\(b\)为\(a\pmod p\) 意义下的逆元,记作\(a^{-1}\)
- 逆元存在定理,存在\(a\)在\(\pmod p\)意义下的逆元\(\iff\) \((a,b)=1\)
- 逆元性质,满足几乎所有分式性质,例如在\(\pmod p\)意义下\(a^{-1}\times b^{-1}=(a\times b)^{-1}\),\(a\times a^{-1}=1\)
- 有理数取模 \(\frac{}{}\)
- 线性求逆元
\(i^{-1}\equiv (p-p/i) \times(p\% i)^{-1}\pmod p\)
\(why?\)
证明:设\(p=a\times i+b\) (\(0\leq\) \(b< i\))
\(a\times i+b=p\)
\(a\times i+b\equiv 0 \pmod p\)
\(-a\times i\equiv b \pmod p\)
\(-a\times b^{-1}\equiv i^{-1} \pmod p\)
\(i^{-1} \equiv (p-a)\times b^{-1} \pmod p\)
也就是\((p\% i)^{-1}\pmod p\)
\(Q.E.D\) - 组合数定义\(C^{m}_{n}=\frac{n!}{m!\times (n-m)!}\)补充定义,若\(m>n\)时\(C^{m}_{n}=0\)
- 组合数的一堆性质
\(C_{n}^{m}=C_{n}^{n-m}\)
\(C_{n}^{m}=C_{n-1}^{m-1}+C_{n-1}^{m}\) - 二项式定理\((1+x)^k=\sum^{k}_{i=0}C_{k}^{i}x^i\)
- 卢卡斯定理,若p为质数\(C_{n}^{m}\equiv C_{n\%p}^{m\%p}\times C_{n/p}^{m/p}\pmod p\)
引理:若\(p\)为质数\((1+x)^p\equiv 1+x^p \pmod p\)
引理证明:因为p为质数,所以当\(2\leq\) \(k< n\)时\(p\mid C_{p}^{k}\)所以引理成立
设\(n=a\times p+b,m=c\times p+d\)(\(0\leq\) \(b< p\) , \(0\leq\) \(d< p\))
\((1+x)^n=\sum _{i=0}^{n}C_{n}^{i}\times x^i\)
\((1+x)^n=(1+x)^{a\times p+b}=((1+x)^p)^a\times (1+x)^b\equiv (1+x^p)^a\times (1+x)^b\equiv\sum_{i=0}^{a}C_{a}^{i}x^{p\times i}\times\sum_{i=0}^{b}C_{b}^{i}x^i \pmod p\)
而\(C_{n}^{m}\)代表的是\(x^m\)的系数,我们发现只能是第一个式子中\(C_{a}^{c}\times x^{p\times c}\)第二个式子中的\(C_{b}^{d}\times x^d\)
故系数为\(C_{a}^{c}\times C_{b}^{d}=C_{n}^{m}\)
也就是说\(C_{n}^{m}=C_{n\%p}^{m\%p}\times C_{n/p}^{m/p}\) - \(Ex lucas\):不保证\(p\)是质数,求\(C_{n}^{m}\%p\)
可以将\(p\)分成质数次幂
\(p=\prod_{i=1}p_i^{\alpha_i}\),我们似乎可以合并
但不幸的是,我 TM并未保证\(\forall i,\alpha_i=1\)所以还不是质数,无法做。
我们只能换而求\(C_{n}^{m}\%p_i^{\alpha_i}\)
怎么办呢?发现\(a\)对\(p\)有逆元的充要条件为
\(gcd(a,p)=1\)
\(\displaystyle C_{n}^{m}\%P^{k}=\displaystyle\frac {\displaystyle\frac {n!}{P^{x}}}{\displaystyle\frac {m!}{P^{y}}\displaystyle\frac {(n-m)!}{P^{z}}}P^{x-y-z}\bmod{P^k}\)
记\(f(n)=\frac {n!}{P^{x}}\)
\(f(n)=f(\lfloor\frac{n}{P}\rfloor)\times(\displaystyle\prod_{i=1,P\displaystyle\nmid i}^{P^k}i)^{\displaystyle\lfloor\frac{n}{P^k}\rfloor}\times \displaystyle\prod_{i=\displaystyle\lfloor\frac{n}{P^k}\rfloor\times P^k,P\displaystyle\nmid i}^{n}i\)
然后怎么求其中的\(x,y,z\)什么的呢
用\(g(n)\)代表\(n!\)里面有多少个\(P\)的因子
\(g(n)=\lfloor \frac nP\rfloor+g(\lfloor \frac nP\rfloor)\)
例题参考洛谷P4720 - 卡特兰数 \(Cat_{0}=1,Cat_{1}=1,Cat_{n}=\sum_{i=0}^{n-1}Cat_{i}\times Cat_{n-i-1}=\frac{C^{n}_{2\times n}}{n+1}=C^{n}_{2n}-C_{n-1}^{2n}\)
- ...待更
例题部分
例一计算系数
根据二项式定理答案为\(C_{k}^{n}\times a^n\times b^m\)
实现方法:预处理阶乘,及其逆元
inline void ginv()
{
inv[0]=1,inv[1]=1;
finv[0]=f[0]=1;
for(int i=2;i<=p+100;i++) inv[i]=(p-p/i)*inv[p%i]%p;
for(int i=1;i<=p+100;i++) f[i]=f[i-1]*i%p,finv[i]=finv[i-1]*inv[i]%p;
}
inline int comb(int n,int m)
{
if(n>m) return 0;
return f[m]*finv[n]%p*finv[m-n]%p;
}
inline int lucas(int n,int m)
{
if(n>m) return 0;
return lucas(n/p,m/p)*comb(n%p,m%p)%p;
}
inline void work()
{
read(a),read(b),read(k),read(n),read(m);
ginv();
printf("%lld\n",qpow(a,n,p)*qpow(b,m,p)%p*lucas(n,k)%p);
}
例二2^k进制数
首先考虑\(2^k\)进制的一位相当于2进制的\(k\)位
那么假如\(k\mid r\),我们可以假设成是有\(\frac{r}{k}\)个\(2^k\)进制数,显然的,由于\(2^k\)有\(2^k\)个基本数码所以我们每次在这\(2^k\)中随便选\(\frac{r}{k}\)个就行,然后给他排个序就行了。
显然我们可以枚举位数,\(i\)答案即为\(C_{2^k-1}^{i}\)
总的答案即为\(\displaystyle \sum _{i=0}^{r/k}C_{2^k-1}^{i}\)
我们在考虑\(k\nmid r\)时,我们考虑的只需要考虑\(\lfloor \frac{r}{k}\rfloor+1\)位的情况就行枚举第一位的数值\(1-(2^{r\ mod\ k}-1)\)此时答案为\(\displaystyle \sum_{i=1}^{2^{r\ mod\ k}-1}C^{i}_{2^k-1-i}\)
最终答案就为\(\displaystyle \sum _{i=0}^{r/k}C_{2^k-1}^{i}+\displaystyle \sum_{i=1}^{2^{r\ mod\ k}-1}C^{i}_{2^k-1-i}\)
注意这道题需要高精
例三 组合
本题同例一模板题
例四 古代猪文
根据相关文献记载,那个朝代流传的猪文文字恰好为远古时期的k分之一,其中k是N的一个正约数(可以是1和N)。
他打算考虑到所有可能的k。
然而从N个文字中保留下N / k个的情况也是相当多的。
可能的k的所有情况数加起来为P的话,那么他研究古代文字的代价将会是G的P次方。
题意实在不好懂。。。
大体就是让你求\(s=\displaystyle \sum _{k\mid n}C_{n}^{k}\)
然后再求\(G^s\pmod p,p\)为质数
由费马小定理\(G^s\equiv G^{s\%(p-1)}\pmod p\)
也就是要求\(\displaystyle \sum _{k\mid n}C_{n}^{k}\%(p-1)\)
然后你就自闭了,因为(p-1)不是质数,没法求逆元。GG本体无解
所以我们想一下怎么yy,我们将\(q=p-1\)分解因数
\(q=\sum_{i=1}p_i^{\alpha_i}\)
后面过程极度舒适因为\(q=p-1=999911659=2\times3\times4679\times35617\)
只需每个模数求一般,用\(crt\)合并就\(ok\)了
例五 Bullcow
我们考虑一个基本题,当这题没有k的限制,我们考虑总共有\(m\)只牛,\(n\)的杜牛,考虑插板在\((m-n)\)个牛中找\(n\)个地方隔开所以答案为\(C_{m-n}^{n}\)
回到此题
当确定了\(i\)个杜牛时,其中任意两个中有的牝牛的个数已确定了。
所以我们考虑假设此时只有\(m-(i-1)\times k\)牝牛所以答案为\(C_{m-(i-1)\times k}^{i}\)
最终答案为\(\displaystyle \sum _{i=0}^{\frac{m}{k}+1}C_{m-(i-1)\times k}^{i}\)
暴力硬跑就行
例六 方程的解数
本题我也不知道为什么是组合数学
\(Meet\ in\ the\ middle\)
折半搜索
具体操作可以,枚举每一个\(x_i\)的值,但肯定是不行的
我们考虑优化。
我们先考虑\(i\in \{1,2,...,\lfloor n/2\rfloor\},x_i\)的取值,求出函数值,保存函数值的个数\(num_i\)
然后枚举\(i\in \{\lfloor n/2\rfloor+1,\lfloor n/2\rfloor+2,...,n\},x_i\)的取值,求出函数值,保存函数值的个数\(num_i\),假如两组值有互为相反数的\(x,-x\),答案应加上\(num_x\times num_{-x}\)
完事了,可以用双指针数组,哈希表,map等实现。
例七 车的放置
我最讨厌明明可以数学方法切,还要\(dp\)的。。。
这题可以不\(dp\)
引理:假如原图是个长方形
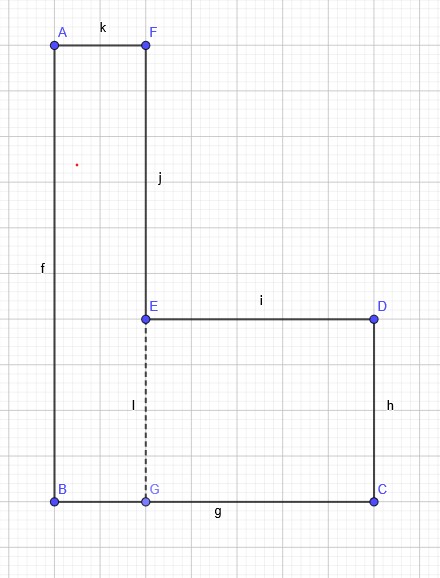
我们设长\(n\),宽\(m\),\(k\)个车
则答案为\(f(n,m,k)=\frac{1}{k}\times\displaystyle \sum_{i=0}^{k-1}(n-i)\times(m-i)\)
我们将一个拐图分成两个长方形图

然后枚举任意一个长方形里的车的个数,假设右面矮的那个有\(i\)个车,则左面有\(k-i\)个车。因为右面一定对左面有影响
所以右面答案:\(f(c,d,i)\)
左面答案:\(f(a,b+d-i,k-i)\)
很好理解吧。。。
例八 数三角形
首先还是一个引理

我们可以发现从\((0,0)\)原点到\((x,y)\)点的线段经过了\(gcd(x,y)+1\)个整点(算\((0,0),(x,y)\))
我们首先不考虑三点共线情况答案是什么?
当然是 \(C_{n\times m}^{3}\)
其次我们考虑平的三点共线
答案是 \(C_{n\times m}^{3}-n\times C_{m}^{3}-m\times C_{n}^{3}\)
最终我们考虑斜着的三点共线
好了,终于到正题了
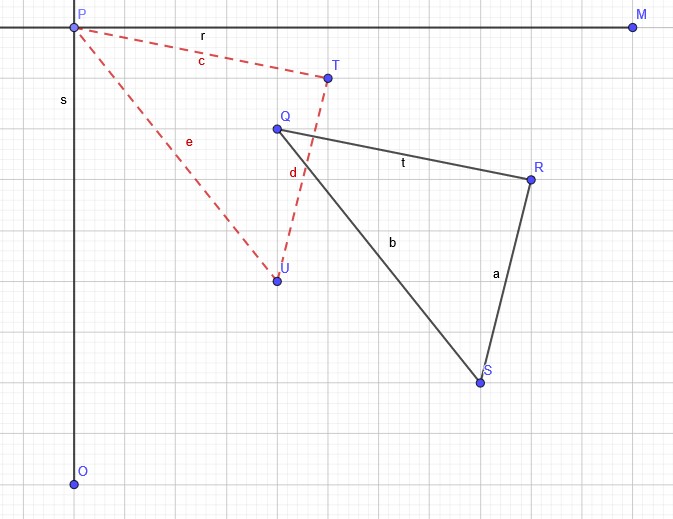
我们都知道一个区域中的三角形一定可以平移到
该区域原点,如图。
所以我们假如他可以三点共线,那么必可以平移到原点,此时我们只要算出整个区域内有多少个这样的三点共线(意思为平移后相同)
然后在算出最远点到原点上有几个整数点\(-2\)(一个是该点,一个是原点),最后刚才两数一乘,答案减去就行了

第一个,有多少个这样的三点共线我们发现,假设区域是\((n,m)\),点是\((x,y)\),一共就有\((n-x+1)\times(m-y+1)\)个
第二个,引理说过应为\(gcd(x,y)-1\)
部分代码
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
ans-=2*(n-i+1)*(m-j+1)*((gcd(i,j)-1));
}
为什么有个2。。。因为
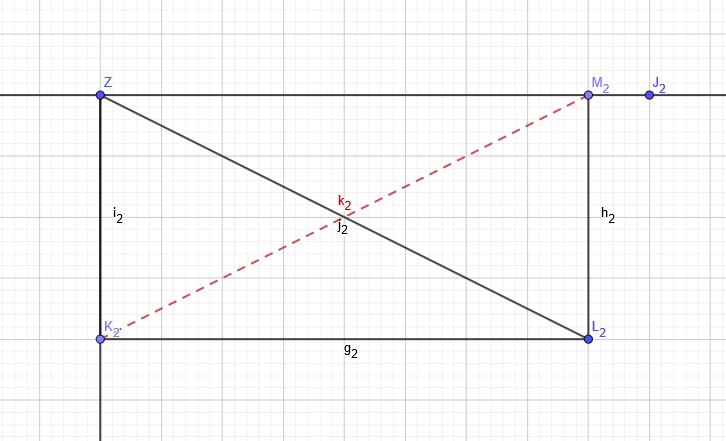
每一个黑色对应一个红色
我在这以前自己做的时候卡了好久。。
例九 combination
同例一
例十 序列统计
假如我们已经确定了序列长\(i\)
那么此时我们求的\(a_i\)单调不减的种类数。
这不好求,我们转化为求\(b_i=a_i+i\)单调增的种类数
所以进一步转换为求在\([L-1,(R+i)]\)中选\(i\)个单调不减的数列
我们类似前面的先随便选,你给他排序的想法,此时答案为\(C_{R+i-L}^{i}\)
总的答案就为\(\displaystyle \sum _{i=1}^{n}C_{R+i-L}^{R-L}\)
怎么求? 这里给出一种几何\(yy\)做法

我们把杨辉三角画出,每个点的值均为其左上,右上的点的权值和。图中红色部分
题目所求类似于图中紫色部分,假如我们要求紫色的和,我们先加上一个\(F_1=C_{x}^{0}=1\),此时我们发现可以连锁反应,最后答案积累到点\(D_2\)上而我们知道\(M_1\)是\(C_{R-L+n}^{R-L}\),不难发现\(D_2\)是\(C_{R-L+n+1}^{R-L+1}\)
最后答案即为\(C_{R-L+n+1}^{R-L+1}-1\)(别忘了最初先加上的1)
例十二 超能粒子炮
题目大意求\(\displaystyle \sum_{i=0}^{k}C_{n}^{i}\%p,p=2333\)
设\(f(n,k)=\sum_{i=0}^{k}C_{n}^{i}\%p\)
由于模数小,首先\(lucas\) 一波
\(f(n,k)=\sum_{i=0}^{k}C_{n\%p}^{i\%p}\times C_{\lfloor n/p\rfloor}^{\lfloor i/p\rfloor}\%p\)
看到了\(i/p\) 我们,再次整除分块一波,就是将\(i/p\)相同的\(i\)分在一块里
我们得到原式为\(f(n,k)=\displaystyle\sum_{t=0}^{\lfloor k/p\rfloor-1}\sum_{i=0}^{p-1}C^{i}_{n\%p}\times C_{n/p}^{t}+\sum_{i=0}^{k\%p}C_{\lfloor n/p\rfloor}^{\lfloor k/p\rfloor}\times C_{n\%p}^{i}\)
整理一下\(f(n,k)=\displaystyle\sum_{t=0}^{\lfloor k/p\rfloor-1}C_{\lfloor n/p\rfloor}^{t}\times \sum_{i=0}^{p-1}C^{i}_{n\%p}+C_{\lfloor n/p\rfloor}^{\lfloor k/p\rfloor}\times\sum_{i=0}^{k\%p} C_{n\%p}^{i}\)
设\(g(n,k)=\displaystyle\sum_{i=0}^{k}C_{n}^{i}\)
现在进行最后一步化简\(f(n,k)=f(\lfloor n/p\rfloor,\lfloor k/p\rfloor)\times g(n\%p,p-1)+C_{\lfloor n/p\rfloor}^{\lfloor k/p\rfloor}\times g(n\%p,k\%p)\)
怎么求\(g(i,j)?\),和\(C_{i}^{j}\)一起\(O(n^2)\)预处理直接求
\(f(n,k)\)直接递归求
例十三 礼物
这题的式子很好想,直接乘法原理
记\(f(x)=\displaystyle \sum_{i=1}^{x}w_i\)
\(\displaystyle\prod _{i=1}^{m} C^{w_i}_{n-f(i-1)}\)
你慌了,因为这个式子似乎无法化简了。
但幸好\(m \leq 5\)\(\times 10^5,O(m)\)硬跑就行
不妙的是,因为模数不为质数,你无法预处理阶乘的逆元
但幸好你会\(exlucas\)直接就切了。。。
例十四 网格
当不限制那条斜线时,
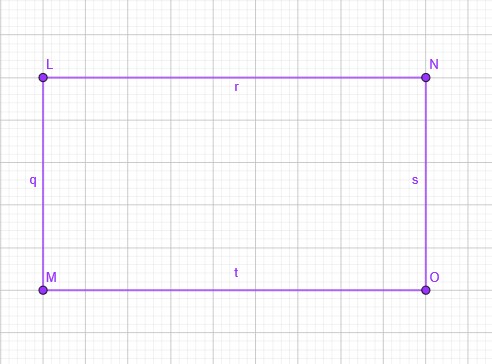
我们答案就为\(C_{n+m}^{n}\)意思就为我们一共有\(n+m\)步,每一步都可能向上,或向右,我们选出有那几步向有,这个走的方法就确定了
但是有限制。。。
我们构造出所到点的关于那条斜线的对称点,然后,规定假如你第一次碰斜线,那么以后你假如向上,你就必须改为向左,反之亦然。

不难证明到对称点的方式与到原终点且经过斜线的方法是一样的,我们只需求出到原终点方法数\(-\)到对称点的方法数就行了。
完了。
其实卡特兰数也可以使用这种类似方法给出大体证明,但在另一侧还需要几步生成函数,这里不讲了。
例十五 有趣的数列
比较好的一道卡特兰数题
\(to\)找规律的我也无法否定,但是假如题目特别猥琐给你了个带系数的答案,你还怎么找规律了呢?
我们首先换一种角度想问题
我们是在将\(1-2n\)按顺序填到数组里,而且每次只能从最靠前的没填过的奇数,偶数位填。我们必须保证任意时刻已填的奇数的个数一定要小于已填的偶数的个数。
哦,这不可以类似我们刚才看的网格那题,该题要求的是向上的步数要在任意时刻小于向左的步数。。。
这才是卡特兰数的模板。
答案即为\(Cat_n=\frac{1}{n+1}\times C_{2n}^{n}\)
但不要忘了他的模数不保证是质数,所以,嘿嘿嘿。
你可以用分解质因数的方法来\(O(n\log n)\)强势x过去。
就是类似
inline void ins(int x)
{
for(register int i=1;i<=tot&&p[i]*p[i]<=x;i++)
if(x%p[i]==0)
{
while(x%p[i]==0)
{
if(!vis[x]&&x<=n){vis[x]=1;return ;}
x/=p[i],b[i]++;
}
}
if(x>1) b[mp[x]]++;
}
inline void del(int x)
{
for(register int i=1;i<=tot&&p[i]*p[i]<=x;i++)
if(x%p[i]==0) while(x%p[i]==0) x/=p[i],b[i]--;
if(x>1) b[mp[x]]--;
}
ins就是乘上一个数。
del就是除以一个数。
显然是对的。。假如你会初一的单项式乘法,除法法则。。
例十六 树屋阶梯
引理:我们考虑假如是一个\(k\)阶树屋,那么要用长方形覆盖他,最少也要\(k\)个。
怎么证?
数归:引理在\(k=1\)时成立
假设引理在\(k=n\)时成立
那么在\(k=n+1\)时答案即为\(y_k=\min_{i=1}^{n}{y_i+y_{n-i}}+1=i+n-i+1=n+1\)
故引理成立。
那么我们就考虑切割树屋。

此时,很明显,类似引理中的\(y_i\),\(Ans_i=\displaystyle\sum_{i=0}^{n}Ans_i\times Ans_{n-i}\)
明显\(Ans_i\),就是卡特兰数
由于\(N\leq500\),我们要高精度求出\(Cat_N=C^{N}_{2N}-C_{N-1}^{2N}\)
也是\(O(n^2)\)求出组合数
The end
完结散花
感谢您看了这篇长达4000+字数的文章。我真的也是废了好大劲肝了好几晚上才写完的。第一次写这么多如有什么错误,不足的地方还请指出。
放一下\(qq:2048455641\)


