[Leetcode] Longest Palindromic Substring

Given a string S, find the longest palindromic substring in S. You may assume that the maximum length of S is 1000, and there exists one unique longest palindromic substring.

 http://blog.csdn.net/hopeztm/article/details/7932245

Solution 1: 以某个元素为中心，分别计算偶数长度的回文最大长度和奇数长度的回文最大长度。时间复杂度O(n^2)，空间O（1）

public String longestPalindrome(String s) {
        if (s == null || s.equals(""))
            return "";
        int N = s.length();
        if (N == 1)
            return s;
        int start = 0;
        int maxLength = 0;

        for (int i = 1; i < N; ++i) {
            // 寻找以i-1,i为中点偶数长度的回文
            int low = i - 1;
            int high = i;
            while (low >= 0 && high < N && s.charAt(low) == s.charAt(high)) {
                low--;
                high++;
            }
            if (high - low - 1 > maxLength) {
                start = low + 1;
                maxLength = high - low - 1;
            }
            //寻找以i为中心的奇数长度的回文
            low = i - 1;
            high = i + 1;
            while (low >= 0 && high < N && s.charAt(low) == s.charAt(high)) {
                low--;
                high++;
            }
            if (high - low - 1 > maxLength) {
                start = low + 1;
                maxLength = high - low - 1;
            }
        }
        return s.substring(start, start + maxLength);
    }

这种方法比较好理解！！！

 

Solution 2: Manacher算法，时间复杂度O(n), 空间复杂度O(n)

 http://blog.csdn.net/a83610312/article/details/8544398

该算法首先对字符串进行预处理，在字符串的每个字符前后都加入一个特殊符号，比如字符串 abcd 处理成 #a#b#c#d#,为了避免处理越界，在字符串首尾加上不同的两个特殊字符(c类型的字符串尾部不用加，因为自带‘\0’)，这样预处理后最终变成$#a#b#c#d#^，经过这样处理后有个好处是原来的偶数长度和奇数长度的回文在处理后的字符串中都是奇数长度。假设处理后的字符串为s                    本文地址

 

对于已经预处理好的字符串我们用数组p[i]来记录以字符S[i]为中心的最长回文子串向左/右扩张的长度（包括S[i]）,以字符串“12212321”为例，p数组如下

s：   $   #  1  #  2  #  2  #  1  #  2  #  3  #  2  #  1  #  ^ 
 p：       1  2  1  2   5  2  1  4  1   2  1  6  1   2  1  2  1

     可以看出，P[i]-1正好是原字符串中回文串的总长度, 如果p数组已知，遍历p数组找到最大的p[i]就可以求出最长回文的长度，也可以求出回文的位置

 

下面给出求p[]数组的方法：

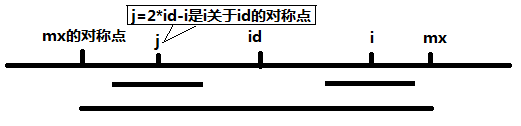
设id是当前求得的最长回文子串中心的位置，mx为当前最长回文子串的右边界（回文子串不包括该右边界），即mx = id + p[id]。记j = 2*id – i ，即 j 是 i 关于 id 的对称点。

 

1、 当i < mx 时，如下图。此时可以得出一个非常神奇的结论p[i] >= min(p[2*id - i], mx - i)，下面我们来解释这个结论

 

如何根据p[j]来求p[i]呢，又要分成两种情况

 

（1.1）当mx – i > p[j], 这时候以S[j]为中心的回文子串包含在以S[id]为中心的回文子串中，由于 i 和 j 对称，以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中，所以 P[i]  至少等于 p[j], 后面的再继续匹配。如下图

注：这里其实p[i]一定等于p[j],后面不用再匹配了。因为如果p[i]后面还可以继续匹配，根据对称性，p[j]也可以继续扩展了

 

 

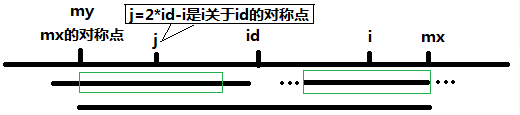
（1.2）当mx – i <= p[j]， 以S[j]为中心的回文子串不完全包含于以S[id]为中心的回文子串中，但是基于对称性可知，下图中两个绿框所包围的部分是相同的，也就是说以S[i]为中心的回文子串，其向右至少会扩张到mx的位置，也就是说 P[i] 至少等于 mx - i，至于mx之后的部分是否对称，就只能老老实实去匹配了。

注：如果mx – i < p[j] ，这时p[i]一定等于mx - i, 因为如果p[i]在mx之后还可以继续匹配，根据对称性，mx之后匹配的点(包括mx)一定会出现在my的前面，这说明p[id]也可以继续扩展了

 

 

2、当i >= mx, 无法对p[i]做更多的假设，只能p[i] = 1,然后再去匹配

package POJ;

public class Main {

    public static void main(String[] args) {
        Main so = new Main();
        System.out.println(so.longestPalindrome("bb"));
    }

    public String longestPalindrome(String s) {
        // Manacher's Algorithm
        if (s == null || s == "")
            return "";
        if (s.length() == 1)
            return s;
        String str = preprocess(s);
        int n = str.length();
        int[] p = new int[n];
        int id = 0, mx = 0;
        for (int i = 1; i < n - 1; ++i) {
            p[i] = mx > i ? Math.min(p[2 * id - i], mx - i) : 1;
            while (str.charAt(i + p[i]) == str.charAt(i - p[i]))
                p[i]++;
            if (i + p[i] > mx) {
                mx = i + p[i];
                id = i;
            }
        }
        int maxLen = 0, index = 0;
        for (int i = 1; i < n - 1; ++i) {
            if (p[i] > maxLen) {
                maxLen = p[i];
                index = i;
            }
        }
        System.out.println("index====" + index);
        System.out.println("maxLen===" + maxLen);

        return s.substring((index - maxLen )/ 2, (index + maxLen) / 2-1);  //这里需要注意的是，不要写成s.substring(index/2 - maxLen/ 2, index/2 + maxLen/ 2-1)
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 //因为int类型的除法会直接去掉小数部分，之前提交也一直因为这个在报错

    }

    // 预处理字符串，abc预处理后变成$#a#b#c#^
    private String preprocess(String s) {
        // TODO Auto-generated method stub
        int len = s.length();
        String res = "";
        res += "$";
        res += "#";
        for (int i = 0; i < len; ++i) {
            res += s.charAt(i);
            res += "#";
        }
        res += "^";
        return res;
    }
}

 

Solution 3: DP

 

package POJ;

public class Main {

    public static void main(String[] args) {
        Main so = new Main();
        System.out.println(so.longestPalindrome("abbacc"));
    }

    public String longestPalindrome(String s) {
        if (s.length() == 0)
            return "";
        if (s.length() == 1)
            return s;
        boolean[][] dp = new boolean[s.length()][s.length()];
        for (int i = 0; i < s.length(); ++i) {
            for (int j = 0; j < s.length(); ++j) {
                if (i >= j)              //当i==j,只有一个字符，肯定是回文；当i>j,认为该段字符串为空，也是回文。
                    dp[i][j] = true;
                else
                    dp[i][j] = false;
            }
        }
        int maxLength = 1;
        int start = 0;

        for (int k = 1; k < s.length(); ++k) {
            for (int i = 0; i + k < s.length(); ++i) {
                int j = i + k;
                if (s.charAt(j) != s.charAt(i)) {
                    dp[i][j] = false;
                } else {
                    dp[i][j] = dp[i + 1][j - 1];   //此时s.charAt(j)==s.charAt(i)
                    if (dp[i][j]) {
                        if (k + 1 > maxLength) {   //k+1即为字符长度
                            maxLength = k + 1;
                            start = i;
                        }
                    }
                }
            }
        }
        return s.substring(start, start + maxLength);
    }
}