Greedy:Linear world(POJ 2674)

　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　   Linear world

　　题目大意：一些人生活在线性世界中，到达线性世界两端就会消失，两个人的前进方向有两个，相遇会改变各自相遇方向，求最后一个人掉下的人的名字和时间。

　　其实这一题就是弹性碰撞的模型，所谓弹性碰撞的模型是两个物体相碰后会改变方向，但是可以看成是各自擦身而过，这个模型可以很快速求解与端点的问题

　　但是这一题还问你一个问题，就是你要找到这个人的名字，这个我一开始，没有想到，只能参考一下别人的代码了

　　http://www.cnblogs.com/gtarcoder/p/4908715.html

　　人的名字坐标 = 最晚消失对应人的坐标+这个人的前进方向的所在的与此人前进方向相反的人的个数

　　现在的问题是：为什么可以这么找？

　　其实我们可以这样看，假设只有一个P，则最晚消失的人将不会受到任何改变。

　　

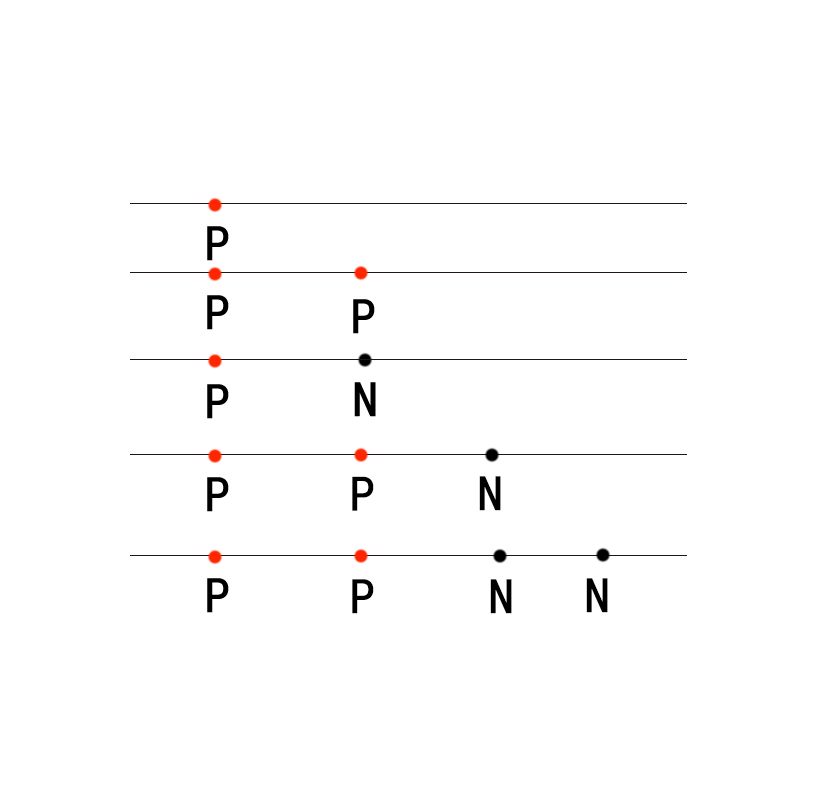
　　我们可以从上图中发现，设时间最晚消失的人一开始是P方向，如果不存在N方向，则最晚消失的人就是最晚消失对应位置，如果不存在P，只存在N，则最晚消失对应的人要往前进一个坐标，如果有两个则前进两个，当P和N同时存在，结论同时成立。所以我们只用找与前进方向相反的人的个数，就可以找到最晚消失的那个人的位置。

　　这个应该是数论问题，但是想了很久还是没有想到有什么好的解释，以后找到就更新一下

  1 #include <iostream>
  2 #include <algorithm>
  3 #include <functional>
  4 #include <math.h>
  5 
  6 using namespace std;
  7 
  8 struct _set
  9 {
 10     bool dir;
 11     double pos;
 12     char name[260];
 13     bool operator < (const _set&x)const
 14     {
 15         return pos < x.pos;
 16     }
 17 }inhabitants[32001], exchange[32001];
 18 
 19 int Search_Name(const int, const int);
 20 void Merge_Sort(const int, const int);
 21 void Merge(const int, const int, const int);
 22 
 23 int main(void)
 24 {
 25     //最大距离位置距离方向有关
 26     double length, rate, max_time;
 27     int sum_people, max_pos, last_stop_pos;
 28     char tmp_dir[2];
 29     while (~scanf("%d", &sum_people))
 30     {
 31         if (sum_people == 0) break;
 32         scanf("%lf%lf", &length, &rate);
 33         getchar();
 34         for (int i = 0; i < sum_people; i++)
 35         {
 36             scanf("%s %lf %s", tmp_dir, &inhabitants[i].pos, inhabitants[i].name);
 37             inhabitants[i].dir = tmp_dir[0] == 'p' || tmp_dir[0] == 'P' ? 1 : 0;
 38         }
 39         sort(inhabitants, inhabitants + sum_people);
 40         //Merge_Sort(0, sum_people - 1);
 41         max_time = -1;
 42         for (int i = 0; i < sum_people; i++)//找到最大的位置
 43         {
 44             if (inhabitants[i].dir == 1)
 45             {
 46                 if ((length - inhabitants[i].pos) / rate> max_time)//正方向
 47                 {
 48                     max_time = (length - inhabitants[i].pos) / rate;
 49                     max_pos = i;
 50                 }
 51             }
 52             else
 53             {
 54                 if (inhabitants[i].pos / rate > max_time)//反方向
 55                 {
 56                     max_time = inhabitants[i].pos / rate;
 57                     max_pos = i;
 58                 }
 59             }
 60         }
 61         last_stop_pos = Search_Name(max_pos, sum_people);
 62         printf("%13.2lf %s\n", floor(100 * max_time) / 100.0, inhabitants[last_stop_pos].name);
 63     }
 64     return EXIT_SUCCESS;
 65 }
 66 
 67 int Search_Name(const int max_pos,const int sum_people)
 68 {
 69     int dir_count = 0;
 70     if (inhabitants[max_pos].dir == 1)
 71     {
 72         for (int i = max_pos + 1; i < sum_people; i++)
 73             if (inhabitants[i].dir == 0)
 74                 dir_count++;
 75         return max_pos + dir_count;
 76     }
 77     else
 78     {
 79         for (int i = 0; i < max_pos; i++)
 80             if (inhabitants[i].dir == 1)
 81                 dir_count++;
 82         return max_pos - dir_count;
 83     }
 84 }
 85 
 86 /*void Merge_Sort(const int left,const int right)
 87 {
 88     int mid = (left + right) / 2;
 89     if (right > left)
 90     {
 91         Merge_Sort(left, mid);
 92         Merge_Sort(mid + 1, right);
 93         Merge(left, mid + 1, right);
 94     }
 95 }
 96 
 97 void Merge(const int left, const int mid, const int right)
 98 {
 99     int pos1 = left, pos2 = mid, l_end = mid - 1, r_end = right, pos_exchange;
100     for (pos_exchange = left; pos1 <= l_end && pos2 <= r_end;)
101     {
102         if (inhabitants[pos1].pos < inhabitants[pos2].pos)
103             exchange[pos_exchange++] = inhabitants[pos1++];
104         else
105             exchange[pos_exchange++] = inhabitants[pos2++];
106     }
107     while (pos1 <= l_end)
108         exchange[pos_exchange++] = inhabitants[pos1++];
109     while (pos2 <= r_end)
110         exchange[pos_exchange++] = inhabitants[pos2++];
111     for (int i = left; i <= right; i++)
112         inhabitants[i] = exchange[i];
113 }*/

　　

　　最后很多人在讨论板说sort会卡时间，我自己试了一下觉得还可以啊，657ms刷掉3000ms的题，编了个Merge_Sort，直接变1200ms.....

　　然后就是这一题，我醉了，P还分大小写，一开始没看题，醉了，欧洲人都喜欢这样玩的吗？

posted @ 2016-01-26 19:33  PhiliAI  阅读(343)  评论(0)  编辑  收藏  举报