【一个蒟蒻的挣扎】模拟赛2解题报告
---恢复内容开始---
今天50分,我自闭
眼瞎看错了一道题,然后两道题的代码都出了点小毛病,自闭
真的竞赛我要这样可以收拾收拾退役了真的,眼睛不能这么瞎了考试莫得人帮忙改了
如果一切都没问题今天应该有130,啊!!!!!!!!!!!!!!!!!
今天两题可以用堆,一题模拟随便写写就过了,(所以我为什么考这么差)
进入正题
题目一览(其实就3道题)(CZR到底是谁这么爱数学和折磨我们)
- 24点
- 小游戏
- 中位数
题1. 24点
题目描述
1.1 Background
CZR很喜欢学数学,但是他数学一直不好,所以他决定玩24点来练习自己.
1.2 Description
然而由于他数学不好,所以他只会加减法:给定四个数,请问是否能通过加法和减法来得到24点.为了训练自己,他每次都会进行5个24点游戏.
1.3 Task
1.3.1 Input
输入有5行,其中每一行为一个24点游戏,为进行24点的4个数字.
1.3.2 Output
输出有5行,其中每一行的游戏中如果能得到24点,则输出’Yes.’;否则输出’No.’.
样例数据
1.4 Sample
1.4.1 Input
1 2 3 4
6 6 6 6
5 6 7 8
5 6 7 6
10 10 5 1
1.4.2 Output
No.
Yes.
No.
Yes.
Yes.
数据范围
对100%的数据,游戏的所有数字≤ 100
题目分析
看到这个“所有数字≤ 100 ”了吗!开不开心!快不快落!随便写个深搜,写个暴力,甚至打个表,就过了啊!!!!!不会超时不会超内存,当真是个水题
(然鹅我把一个减号打成了加号WA了5个点自闭)
说说我的思路啊, 输入有5行,那么在一个for循环里面写;对于输入的4个数,我们开一个数组,记录每一个数的所有情况(二维,挺小的,【5】【31】就行,反正只有加减随便写),然后4个for循环模拟累加,最后在到达第4个点的时候扫一遍看有没有==24的,有就输出“Yes.”没有就输出“No.”(看清楚这里,首字母大写,有个句号)
是真的没啥好讲的,简简单单,我来记一下其他人的思路(应该可以的吧...)
最引人注目的tcr大佬,

妙啊!!!!!!!!!简洁明了还不容易错,tqltql
kqy和jyy似乎都是深搜,这种很正常的思路也就不说了大家差不多(耗时间和耗空间的不太一样大体思路差别不大我觉得)
好的上代码
#include<iostream> #include<cstdio> #include<cstring> using namespace std; int t1=1; int add[5][31],jian[5][31]; void ss(int t,int k) { for (int i=1; i<=t1; i++) add[t][i]=add[t-1][i]+k; for (int i=t1+1; i<=t1*2; i++) add[t][i]=jian[t-1][i-t1]+k; for (int i=1; i<=t1; i++) jian[t][i]=jian[t-1][i]-k; for (int i=t1+1; i<=t1*2; i++) jian[t][i]=add[t-1][i-t1]-k; if (t==4) { int flag=0; for (int i=1; i<=t1*2; i++) if (add[t][i]==24||jian[t][i]==24) { cout<<"Yes."; flag=1; break; } if (flag==0) cout<<"No."; } t1*=2; } int main() { //freopen("24.in","r",stdin); //freopen("24.out","w",stdout); int a[5]; for (int ii=1; ii<=5; ii++) { t1=1; memset(add,0,sizeof(add)); memset(jian,0,sizeof(jian)); cin>>a[1]>>a[2]>>a[3]>>a[4]; add[1][1]=a[1]; jian[1][1]=-a[1]; for (int i=2; i<=4; i++) ss(i,a[i]); cout<<endl; } //fclose(stdin); //fclose(stdout); return 0; }
题2.小游戏
题目描述
2.1 Background
CZR虽然已经是个大学生了,但是他还是喜欢在家里偷偷玩跳格子.
2.2 Description
CZR的家里有连续的N + 1块地砖,编号为0到N,他在每一块地砖上
都写上了一个数字.
一开始他在0号地砖,这块地砖的分数为0,每次他都会后面跳一步
但是他不一定需要跳到最后.
因为他跳远能力不行,所以他一步只能往后跳L到R个格子,也就是说
在地砖i时,他只能跳到地砖i + L到i + R中的一块地砖.
他进行一次游戏的分数总和是他跳到的所有地砖的分数之和.
他现在想获得最大的分数,来证明自己的数学能力很强,所以他需要
知道最大分数是多少.
2.3 Task
2.3.1 Input
输入的第一行为一个数N,表示地砖个数.
第二行有两个数L和R,表示他一次跳远能跳的范围.
第三行有N个正整数,分别表示1号地砖到N号地砖上的分数.
2.3.2 Output
输出只有一行,为能跳出的最大分数.
样例数据
2.4 Sample
2.4.1 Input
5
1 2
1 2 3 4 5
2.4.2 Output
15
数据范围
2.6 Constraint
对50%的数据,N ≤ 1000.
对于100%的数据,N ≤ 5 ∗ 105.
可能存在负数
题目分析
啊稍微难了一点呢,不过也还行,看起来像不像动规?
不要退缩,这题难的并不是动规
我们很容易就能发现(发现不了拿着草稿纸推一遍样例绝对能发现):
令F[i]表示CZR跳到第i个格子上时能够获得的最大分数
那么,F[i]=max{F[i-l],...F[i-r}+a[i]; //注意!题目上说的是可以跳到第 i + l 到 第 i + r !不是第 i + l 或 第 i + r,就这个把我坑惨了这题一分没有
题面上说,“对50%的数据,N ≤ 1000.”,它肯定不是胡编的数字,我们如果求上面这个式子,那么它的时间复杂度为O(N^2),也就是说只能过百分之50的点(之后的就TLE啦)
那么正解是什么呢?(别想了这个式子肯定还是要有的必须推出来而且必!须!推!对!)
我们再重新看一下这个问题,由于这个 i 要取遍1-n,所以我们可以简化为要求一个长度固定的区间的最大值
于是老师给出了如下几种优化方式(是的优化一下就可以了)
- 单调队列 时间复杂度O( n ) <------正解
- ST表 时间复杂度O(n log n + n )
- 堆 时间复杂度O(n log n)
先说 单调队列:
固定区间的最大值,单调队列很好写也很好想,只要分为进队和出队两个步骤,扫过去就好了(然鹅老师的代码我没看懂,要再多琢磨琢磨,其实我觉得堆要好懂一点(小声))
再说 ST表
![]()
(直接引用过来了(我太懒了),ST表我当时没怎么听懂,也是要再琢磨的)
最后说 堆:(万众瞩目(不是))

至于堆的基本操作,我是会了的,STL也可以用(不过有一、、麻烦),洛谷模板题可以看一看(堆学一学还是蛮好的)https://www.luogu.org/problem/P3378
题3.中位数
题面描述
3.1 Background
虽然CZR数学很烂,但是他还是想证明一下自己的数学能力,今天他
想要表演一下瞬间计算中位数.
3.2 Description
一开始集合为空,每次有两个操作:
1 x:告诉CZR当前集合中再加入一个数x.
2 :询问CZR当前集合的中位数是多少.
3.3 Task
3.3.1 Input
输入的第一行为一个数N,表示操作数量.
接下来的N行,每行有一个操作,如题目所示.
3.3.2 Output
对于每一个询问操作,请输出当前的中位数.
请一行输出一个答案.
对于小数请只输出十分位.
样例数据
3.4 Sample
3.4.1 Input
7
1 1
2
6
1 2
1 3
2
1 4
2
3.4.2 Output
1 2
2.5
数据范围
3.6 Constraint
对于30%的数据,N ≤ 1000.
对于100%的数据,N ≤ 5 ∗ 105.正整数,在 int 范围内
题目分析
看到那个30%的数据了吗,就是留来我们骗分的,sort会不会打,一遍就过,30分到手(注意输出小数的时候,".0"是作为整数的小数点后不要)
那么正解是什么呢,还是堆
我们维护两个堆,一个大根堆和一个小根堆
大根堆存储小的数据,小根堆存储大的数据
我们看一下下面这个图
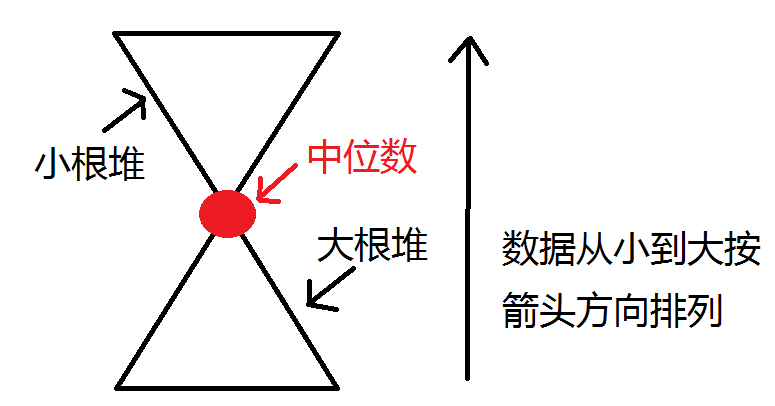
我们每次保证插入的元素使小根堆和大根堆的大小不超过1,并且满足堆的性质,那么我们的答案中位数就一定是在某一个堆堆顶或是两个堆的堆顶平均值
剩下的一些基本操作就不说了,同上题(我也不明白为什么我们并没有上堆而考了堆)
代码依旧——
没有,改天我自己写,老师的代码用的STL我并不是太懂
总而言之,这篇题解可能还需要日后的修正(耗时1-2小时)
但是现在,OVER!
完结撒花!(看不懂来找我)(其实你更应该找老师)
感谢观看 ありがとうございます


 浙公网安备 33010602011771号
浙公网安备 33010602011771号