3Sum
Given an array S of n integers, are there elements a, b, c in S such that a + b + c = 0? Find all unique triplets in the array which gives the sum of zero.
Note: The solution set must not contain duplicate triplets.
For example, given array S = [-1, 0, 1, 2, -1, -4], A solution set is: [ [-1, 0, 1], [-1, -1, 2] ]
分析:
方法一:暴力解法时间复杂度为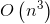 ,肯定超时
,肯定超时
方法二:先将数组排序,然后依次遍历,每次固定一个值,使用两个指针一前一后遍历固定值之后的元素,注意避免重复元素,
代码一:
class Solution(object):
def threeSum(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
nums.sort()
res = []
for i in range(len(nums)-2):
l = i+1
r = len(nums)-1
while l < r:
while l < r and nums[i]+nums[l]+nums[r] == 0:
res_tmp = [nums[i],nums[l],nums[r]]
if res_tmp not in res:
res.append(res_tmp)
while l < r and nums[l+1] == nums[l]:
l += 1
while l < r and nums[r-1] == nums[r]:
r -= 1
l += 1
r -= 1
while l < r and nums[i]+nums[l]+nums[r] > 0:
r -= 1
while l < r and nums[i]+nums[l]+nums[r] < 0:
l += 1
return res
此代码最终也是超时
代码二:
class Solution(object):
def threeSum(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
size = len(nums)
ans = []
if size <= 2:
return ans
nums.sort()
i = 0
while i < size -2:
tmp = 0 - nums[i]
j = i + 1
k = size -1
while j < k:
if nums[j] + nums[k] < tmp:
j += 1
elif nums[j] + nums[k] > tmp:
k -= 1
else:
ans.append([nums[i],nums[j],nums[k]])
j += 1
k -= 1
while j < k:
if nums[j] != nums[j - 1]:
break
if nums[k] != nums[k + 1]:
break
j += 1
k -= 1
i += 1
while i < size - 2:
if nums[i] != nums[i - 1]:
break
i += 1
return ans
此代码可以AC,注意和代码一做对比。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号