B-box Loss of Detection
目标检测作为一种经典的CV任务,大致可以认为是三个子任务的集合:1、确定目标大概位置;2、分类出目标类别;3、回归出检测框的宽高。
这三种子任务分别需要对应损失函数的反向传播来学习。本文介绍的b-box回归损失函数主要是面向第三个子任务而设计的损失函数。
IOU
原文链接:[1608.01471] UnitBox: An Advanced Object Detection Network (arxiv.org)
全称Intersection Over Union,即交并比。计算预测框和标注框(即GT框)的交并比,就可以知道它们的“贴合”程度好不好,作为调整模型的指导。
如下图所示,计算两个b-box之间交集部分的面积比并集的面积
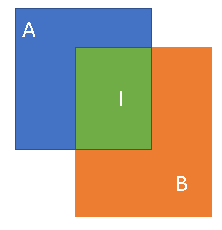
IOU=绿色面积/(蓝色面积+绿色面积+橙色面积)
而IOU loss可以简单表示为: $$L_{IOU}=1-IOU$$
简单python实现如下
#!/usr/bin/env python
# encoding: utf-8
def compute_iou(rec1, rec2):
"""
computing IoU
:param rec1: (y0, x0, y1, x1), which reflects
(top, left, bottom, right)
:param rec2: (y0, x0, y1, x1)
:return: scala value of IoU
"""
# computing area of each rectangles
S_rec1 = (rec1[2] - rec1[0]) * (rec1[3] - rec1[1])
S_rec2 = (rec2[2] - rec2[0]) * (rec2[3] - rec2[1])
# computing the sum_area
sum_area = S_rec1 + S_rec2
# find the each edge of intersect rectangle
left_line = max(rec1[1], rec2[1])
right_line = min(rec1[3], rec2[3])
top_line = max(rec1[0], rec2[0])
bottom_line = min(rec1[2], rec2[2])
# judge if there is an intersect
if left_line >= right_line or top_line >= bottom_line:
return 0
else:
intersect = (right_line - left_line) * (bottom_line - top_line)
return (intersect / (sum_area - intersect))*1.0
if __name__=='__main__':
rect1 = (661, 27, 679, 47)
# (top, left, bottom, right)
rect2 = (662, 27, 682, 47)
iou = compute_iou(rect1, rect2)
print(iou)
GIOU
IOU虽然简单,但有一些明显的缺点:当两个框没有任何交集时,IOU为0,IOU loss会一直为1。无法反应出检测框与GT框之间的距离,从而导致:只要两个框没有交集,IOU loss就恒等于1,则无论朝哪个方向优化,IOU loss都不会下降,此时的IOU loss失去了指导性。GIOU就是在IOU的基础上做了一些改进。
算法描述为:

图示如下:
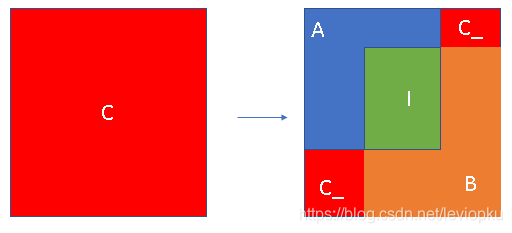
在IOU的基础上找到一个“全局框”C,这个全局框能够刚好把两个b-box装进去,这样就多一部分面积C_。
根据上图表示:GIOU = IOU - C_ / C
GIOU loss可以简单表示为: $$L_{GIOU}=1-GIOU$$ 即: $$L_{GIOU}=1-IOU+C_{-}/C$$
在两个b-box没有交集的情况下:
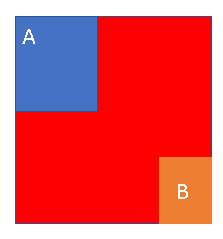
可以看到GIOU会随两个框之间的距离变化而变化,从而反应到loss上,从而指导预测框的移动方向。
但是,当两个框属于包含关系时,GIOU会退化成IOU,无法区分其相对位置关系。
python实现如下:
def calculate_giou(box_1, box_2):
"""
calculate giou
:param box_1: (x0, y0, x1, y1)
:param box_2: (x0, y0, x1, y1)
:return: value of giou
"""
# calculate area of each box
area_1 = (box_1[2] - box_1[0]) * (box_1[3] - box_1[1])
area_2 = (box_2[2] - box_2[0]) * (box_1[3] - box_1[1])
# calculate minimum external frame
area_c = (max(box_1[2], box_2[2]) - min(box_1[0], box_2[0])) * (max(box_1[3], box_2[3]) - min(box_1[1], box_2[1]))
# find the edge of intersect box
top = max(box_1[0], box_2[0])
left = max(box_1[1], box_2[1])
bottom = min(box_1[3], box_2[3])
right = min(box_1[2], box_2[2])
# calculate the intersect area
area_intersection = (right - left) * (bottom - top)
# calculate the union area
area_union = area_1 + area_2 - area_intersection
# calculate iou
iou = float(area_intersection) / area_union
# calculate giou(iou - (area_c - area_union)/area_c)
giou = iou - float((area_c - area_union)) / area_c
return giou
DIOU
原文链接: [1911.08287] Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression (arxiv.org)
在GIOU的基础上进一步强调了距离的重要性,直接算出一个中心点的距离相对于框规模的一个比值。
公式为:
跟GIOU loss相比只是替换了最后一项。最后一项是如何计算的?看图:

跟GIOU一样,DIOU还是需要找到最小包围框C(注意大小写),然后c作为C的对角线长度。图中的d表示两个b-box中心点连线的长度。则最后一项可解读为:中心连线的长度d与最小包围框C对角线长度c的比值的平方。这里为啥加个平方呢?是因为计算距离和长度的时候需要开根号,这里加平方其实是减少开根号的运算步骤。
DIOU Loss具有以下特性:
- DIOU与IOU、GIOU一样具有尺度不变性;
- DIOU与GIOU一样在与目标框不重叠时,仍然可以为边界框提供移动方向;
- DIOU可以直接最小化两个目标框的距离,因此比GIOU Loss收敛快得多;
- DIOU在包含两个框水平/垂直方向上的情况回归很快,而GIOU几乎退化为IOU;
- 当预测框和真实框完全重合时, $$L_{IOU}=L_{GIOU}=L_{DIOU}=0$$
- 当预测框和真实框不相交时, $$L_{GIOU}=L_{DIOU}→2$$
python实现如下:
def calculate_diou(box_1, box_2):
"""
calculate diou
:param box_1: (x0, y0, x1, y1)
:param box_2: (x0, y0, x1, y1)
:return: value of diou
"""
# calculate area of each box
area_1 = (box_1[2] - box_1[0]) * (box_1[3] - box_1[1])
area_2 = (box_2[2] - box_2[0]) * (box_1[3] - box_1[1])
# calculate center point of each box
center_x1 = (box_1[2] - box_1[0]) / 2
center_y1 = (box_1[3] - box_1[1]) / 2
center_x2 = (box_2[2] - box_2[0]) / 2
center_y2 = (box_2[3] - box_2[1]) / 2
# calculate square of center point distance
p2 = (center_x2 - center_x1) ** 2 + (center_y2 - center_y1) ** 2
# calculate square of the diagonal length
width_c = max(box_1[2], box_2[2]) - min(box_1[0], box_2[0])
height_c = max(box_1[3], box_2[3]) - min(box_1[1], box_2[1])
c2 = width_c ** 2 + height_c ** 2
# find the edge of intersect box
top = max(box_1[0], box_2[0])
left = max(box_1[1], box_2[1])
bottom = min(box_1[3], box_2[3])
right = min(box_1[2], box_2[2])
# calculate the intersect area
area_intersection = (right - left) * (bottom - top)
# calculate the union area
area_union = area_1 + area_2 - area_intersection
# calculate iou
iou = float(area_intersection) / area_union
# calculate diou(iou - p2/c2)
diou = iou - float(p2) / c2
return diou
pytorch实现如下:
def diou(bboxes1, bboxes2):
bboxes1 = torch.sigmoid(bboxes1)
bboxes2 = torch.sigmoid(bboxes2)
rows = bboxes1.shape[0]
cols = bboxes2.shape[0]
cious = torch.zeros((rows, cols))
if rows * cols == 0:
return cious
exchange = False
if bboxes1.shape[0] > bboxes2.shape[0]:
bboxes1, bboxes2 = bboxes2, bboxes1
cious = torch.zeros((cols, rows))
exchange = True
w1 = torch.exp(bboxes1[:, 2])
h1 = torch.exp(bboxes1[:, 3])
w2 = torch.exp(bboxes2[:, 2])
h2 = torch.exp(bboxes2[:, 3])
area1 = w1 * h1
area2 = w2 * h2
center_x1 = bboxes1[:, 0]
center_y1 = bboxes1[:, 1]
center_x2 = bboxes2[:, 0]
center_y2 = bboxes2[:, 1]
inter_l = torch.max(center_x1 - w1 / 2,center_x2 - w2 / 2)
inter_r = torch.min(center_x1 + w1 / 2,center_x2 + w2 / 2)
inter_t = torch.max(center_y1 - h1 / 2,center_y2 - h2 / 2)
inter_b = torch.min(center_y1 + h1 / 2,center_y2 + h2 / 2)
inter_area = torch.clamp((inter_r - inter_l),min=0) * torch.clamp((inter_b - inter_t),min=0)
c_l = torch.min(center_x1 - w1 / 2,center_x2 - w2 / 2)
c_r = torch.max(center_x1 + w1 / 2,center_x2 + w2 / 2)
c_t = torch.min(center_y1 - h1 / 2,center_y2 - h2 / 2)
c_b = torch.max(center_y1 + h1 / 2,center_y2 + h2 / 2)
inter_diag = (center_x2 - center_x1)**2 + (center_y2 - center_y1)**2
c_diag = torch.clamp((c_r - c_l),min=0)**2 + torch.clamp((c_b - c_t),min=0)**2
union = area1+area2-inter_area
u = (inter_diag) / c_diag
iou = inter_area / union
dious = iou - u
dious = torch.clamp(dious,min=-1.0,max = 1.0)
if exchange:
dious = dious.T
return torch.sum(1-dious)
CIOU
CIOU的全程是:Complete-IOU。公式如下:
可以发现,这就是DIOU加了最后一项,即调整长宽比的loss项。只需要了解 $$αV$$即可以了解CIOU,先看V,即Consistency of Aspect Ratio:
假设预测框和GT框的宽长比不一致,则V会很大。再看一个trade-off参数α:
由α可以看出,当IOU小于0.5的时候,CIOU就变成了DIOU。IOU越大,α就越接近1。
那么,当IOU很大的情况下,\(\frac{ρ^2(p, p^{gt})}{c^2}\)变为0(中心点重合),这个时候需要调节长宽比了。DIOU在这个时候,loss的梯度也变小了(只靠IOU loss的部分在传递梯度),而CIOU可以依靠最后一项继续保持loss的梯度,使得检测器能够迅速调整好自己与GT框拥有一样的宽高比。
辅以一张对比图来说明:

第一排是GIOU,第二排是CIOU,原点处的绿色框是GT框,黑色框是anchor框,红色框是预测框。可以看到,在预测框和GT框没有交集(即IOU=0)的情况下,GIOU和CIOU都有知道检测框移动的能力。此时GIOU从位置、宽高比、size等角度调整预测框,而CIOU是迅速拉回位置(不怎么动预测框的形状),因此CIOU可以比GIOU更快拉回预测框使其IOU>0。等IOU>0以后,CIOU迅速调整size规模。等IOU>0.5以后,CIOU的宽高比部分开始作为梯度传播的主要部分,使得预测框和GT框有用一样的宽高比。
pytorch实现如下:
def ciou(bboxes1, bboxes2):
bboxes1 = torch.sigmoid(bboxes1)
bboxes2 = torch.sigmoid(bboxes2)
rows = bboxes1.shape[0]
cols = bboxes2.shape[0]
cious = torch.zeros((rows, cols))
if rows * cols == 0:
return cious
exchange = False
if bboxes1.shape[0] > bboxes2.shape[0]:
bboxes1, bboxes2 = bboxes2, bboxes1
cious = torch.zeros((cols, rows))
exchange = True
w1 = torch.exp(bboxes1[:, 2])
h1 = torch.exp(bboxes1[:, 3])
w2 = torch.exp(bboxes2[:, 2])
h2 = torch.exp(bboxes2[:, 3])
area1 = w1 * h1
area2 = w2 * h2
center_x1 = bboxes1[:, 0]
center_y1 = bboxes1[:, 1]
center_x2 = bboxes2[:, 0]
center_y2 = bboxes2[:, 1]
inter_l = torch.max(center_x1 - w1 / 2,center_x2 - w2 / 2)
inter_r = torch.min(center_x1 + w1 / 2,center_x2 + w2 / 2)
inter_t = torch.max(center_y1 - h1 / 2,center_y2 - h2 / 2)
inter_b = torch.min(center_y1 + h1 / 2,center_y2 + h2 / 2)
inter_area = torch.clamp((inter_r - inter_l),min=0) * torch.clamp((inter_b - inter_t),min=0)
c_l = torch.min(center_x1 - w1 / 2,center_x2 - w2 / 2)
c_r = torch.max(center_x1 + w1 / 2,center_x2 + w2 / 2)
c_t = torch.min(center_y1 - h1 / 2,center_y2 - h2 / 2)
c_b = torch.max(center_y1 + h1 / 2,center_y2 + h2 / 2)
inter_diag = (center_x2 - center_x1)**2 + (center_y2 - center_y1)**2
c_diag = torch.clamp((c_r - c_l),min=0)**2 + torch.clamp((c_b - c_t),min=0)**2
union = area1+area2-inter_area
u = (inter_diag) / c_diag
iou = inter_area / union
v = (4 / (math.pi ** 2)) * torch.pow((torch.atan(w2 / h2) - torch.atan(w1 / h1)), 2)
with torch.no_grad():
S = (iou>0.5).float()
alpha= S*v/(1-iou+v)
cious = iou - u - alpha * v
cious = torch.clamp(cious,min=-1.0,max = 1.0)
if exchange:
cious = cious.T
return torch.sum(1-cious)
EIOU
原文链接:https://arxiv.org/pdf/2101.08158.pdf
CIOU Loss虽然考虑了边界框回归的重叠面积、中心点距离、纵横比。但是通过其公式中的v反映的纵横比的差异,而不是宽高分别与其置信度的真实差异,所以有时会阻碍模型有效的优化相似性。针对这一问题,有学者在CIOU的基础上将纵横比拆开,提出了EIOU Loss,并且加入Focal聚焦优质的锚框。
EIOU的惩罚项是在CIOU的惩罚项基础上将纵横比的影响因子拆开分别计算目标框和锚框的长和宽,该损失函数包含三个部分:重叠损失,中心距离损失,宽高损失,前两部分延续CIOU中的方法,但是宽高损失直接使目标盒与锚盒的宽度和高度之差最小,使得收敛速度更快。惩罚项公式如下:
其中\(C_{w}\) 和\(C_{h}\)是两个box的最小外接矩形的宽和高。
考虑到BBox的回归中也存在训练样本不平衡的问题,即在一张图像中回归误差小的高质量锚框的数量远少于误差大的低质量样本,质量较差的样本会产生过大的梯度影响训练过程。作者在EIOU的基础上结合Focal Loss提出一种Focal EIOU Loss,梯度的角度出发,把高质量的锚框和低质量的锚框分开,惩罚项公式如下:
\(γ\)为控制异常值抑制程度的参数。该损失中的Focal与传统的Focal Loss有一定的区别,传统的Focal Loss针对越困难的样本损失越大,起到的是困难样本挖掘的作用;而根据上述公式:IOU越高的损失越大,相当于加权作用,给越好的回归目标一个越大的损失,有助于提高回归精度。
参考资料
https://blog.csdn.net/leviopku/article/details/114655338
https://zhuanlan.zhihu.com/p/270663039


