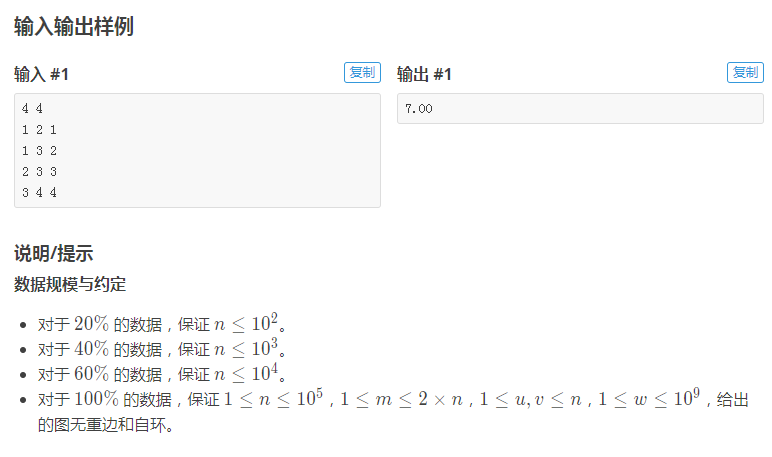
绿豆蛙的归宿（别问我为什么会写这玩意）

声明一下，概率与期望这块属实没有看懂，如果有什么唐氏错误多多包容

正推

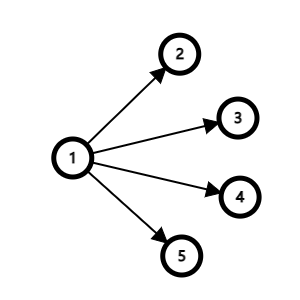
不很显然，对于边(i,j)，j的期望值是i的期望值加上边权除以i的出度(从i出发边的条数)，我对于这个的理解是假设从i出发有k条边，j是其中一个，那么到j的可能就是
\(\frac{1}{k}\) 即\(\frac{1}{out[i]}\)
所以会有 \(f[j]+=\frac{f[i]}{out[i]}\)
又因为已经经过这个边，所以还有
\(f[j]+=\frac{p[i]*w}{out[i]}\)
其中p[i]表示从1到i的概率，p[1]=1,\(p[j]=\sum\frac{p[i]}{out[i]}[w！=0]\)
（实际上就是根据期望的线性思想，利用\(f[i]=\sum{(f[i-1]+w)*p[i]}\)）

看的DZ的

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+100;
struct node{
	int from;
	int to;
	int w;
}edge[N];
double degree[N],out[N],head[N],p[N];
double f[N];
queue<int> q;
int n,m,cnt;
void add(int from,int to,int w){
	cnt++;
	edge[cnt].from=head[from];
	edge[cnt].to=to;
	edge[cnt].w=w;
	head[from]=cnt;
	degree[to]++,out[from]++;
}
int main(){
	int from,to,w;
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		cin>>from>>to>>w;
		add(from,to,w);
	}
	for(int i=1;i<=n;i++){
		if(!degree[i]) q.push(i);
	}
	p[1]=1;
	while(!q.empty()){
		int e=q.front();
		q.pop();
		for(int i=head[e];i;i=edge[i].from){
			int to=edge[i].to;
			f[to]+=(f[e]+edge[i].w*p[e])/out[e];
			p[to]+=p[e]/out[e];
			degree[to]--;
			if(degree[to]==0) q.push(to);
		} 
	}
	cout<<setprecision(2)<<fixed<<f[n]<<endl;
}

逆推

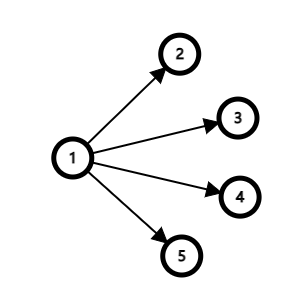
根据正推和分析，实际上我们会发现，需要用到p数组的原因是我们实际上将一个点的期望值拆给了其他与它相连的点(如图中1拆给了2345，p为1/4)，那我们能不能反过来，将2345的期望值加给1呢？很显然是可以的，这就是逆推，
首先，反向建边

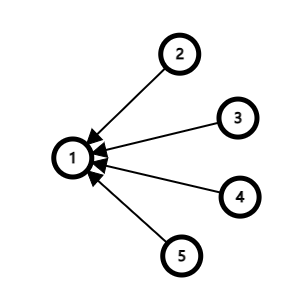
那么对于一条原边(i,j)，i的期望值就是j的期望值和边权的加和除以i的出度
\(f[i]+=(f[j]+edge[i].w)/out[i]\) (这里的i，j和建边的i，j是反过来的)

然后就没了

逆推

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+100;
struct node{
	int from;
	int to;
	int w;
}edge[N];
int degree[N],out[N],head[N];
double f[N];
queue<int> q;
int n,m,cnt;
void add(int from,int to,int w){
	cnt++;
	edge[cnt].from=head[from];
	edge[cnt].to=to;
	edge[cnt].w=w;
	head[from]=cnt;
	degree[to]++,out[to]++;
}
int main(){
	int from,to,w;
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		cin>>from>>to>>w;
		add(to,from,w);
	}
	q.push(n);
	while(!q.empty()){
		int e=q.front();
		q.pop();
		for(int i=head[e];i;i=edge[i].from){
			int to=edge[i].to;
			f[to]+=(f[e]+edge[i].w)/out[to];
			degree[to]--;
			if(degree[to]==0) q.push(to);
		} 
	}
	cout<<setprecision(2)<<fixed<<f[1]<<endl;
}