难存的情缘&货车运输
事先说明,参考的oceans_of_stars,顺便%一下(有事他背锅)
一个求最大,一个求最小,没啥好说的,拿难存的情缘举例说明边权如何转点权
一天机房的夜晚,无数人在MC里奋斗着。。。
大家都知道矿产对于MC来说是多么的重要,但由于矿越挖越少,勇士们不得不跑到更远的地方挖矿,但这样路途上就会花费相当大的时间,导致挖矿效率低下。
cjj提议修一条铁路,大家一致同意。
大家都被CH分配了一些任务:
zjmfrank2012负责绘制出一个矿道地图,这个地图包括家(当然这也是一个矿,毕竟不把家掏空我们是不会走的),和无数个矿,所以大家应该可以想出这是一个无向无环图,也就是一棵树。
Digital_T和cstdio负责铺铁路。。所以这里没他们什么事,两位可以劳作去了。
这个时候song526210932和RMB突然发现有的矿道会刷怪,并且怪的数量会发生变化。作为采矿主力,他们想知道从一个矿到另一个矿的路上哪一段会最困难。。。(困难值用zjm的死亡次数表示)。
输入格式
输入文件的第一行有一个整数N,代表矿的数量。矿的编号是1到N。
接下来N-1行每行有三个整数a,b,c,代表第i号矿和第j号矿之间有一条路,在初始时这条路的困难值为c。
接下来有若干行,每行是“CHANGE i ti”或者“QUERY a b”,前者代表把第i条路(路按所给顺序从1到M编号)的困难值修改为ti,后者代表查询a到b所经过的道路中的最大困难值。
输入数据以一行“DONE”结束。
输出格式
对每个“QUERY”操作,输出一行一个正整数,即最大困难值。
样例
样例输入
3
1 2 1
2 3 2
QUERY 1 2
CHANGE 1 3
QUERY 1 2
DONE
样例输出
1
3
数据范围与提示
对于60%的数据,1<=N<=50
对于100%的数据,1<=N<=10000,1<=c<=1000000,1<=操作次数<=100000
最主要的问题是,如何把边权转点权,以及如何去将修改边转化为修改点
有一个方法就是将边权赋给儿子(边两端中深度较大的那个点)
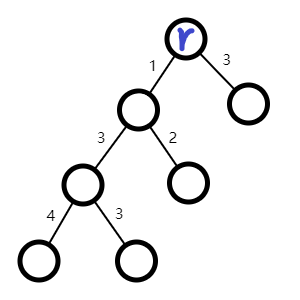
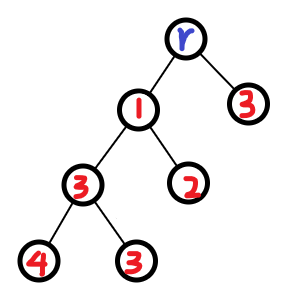
对应代码
void dfs1(int now){
son[now]=-1;
siz[now]=1;
for(int i=head[now];i;i=edge[i].from){
int to=edge[i].to;
if(dep[to]) continue;
a[to]=edge[i].w;//这里
dep[to]=dep[now]+1;
fa[to]=now;
dfs1(to);
siz[now]+=siz[to];
if(son[now]==-1||siz[to]>siz[son[now]]) son[now]=to;
}
}
但这样就有两个问题
1.按树剖求路径最大会多算
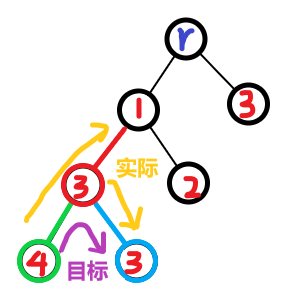
我的本意是想要求4,3与3,3的边的最大值,但实际上还与1,3这条边进行了比较,这会导致误差
所以我们要去掉这个点,实际上也很好像想(不好想)因为这个点的下标一定是两个点跳到同一重链后那个深度浅的点的dfn值,只需要给它+1,就可以解决了
2.对应点,我们存一下每个边的编号,然后修改的的点一定是对应边中深度深的那个点,也可以在一开始的编号中记录一下,都是一样的
cnt1++;
add(from,to,w);
add(to,from,w);
line[cnt1].from=from;
line[cnt1].to=to;
line[cnt1].w=w;
//记录边的编号
cin>>from>>to;
int dian=0;
if(dep[line[from].from]>dep[line[from].to]){
dian=line[from].from;
}
else dian=line[from].to;
update(1,dfn[dian],to);
//找深度深的点
void dfs1(int now){
son[now]=-1;
siz[now]=1;
for(int i=head[now];i;i=edge[i].from){
int to=edge[i].to;
if(dep[to]) continue;
a[to]=edge[i].w;
dian[edge[i].id]=to;//这里
dep[to]=dep[now]+1;
fa[to]=now;
dfs1(to);
siz[now]+=siz[to];
if(son[now]==-1||siz[to]>siz[son[now]]) son[now]=to;
}
}
然后就没了
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define lson id<<1
#define rson id<<1|1
const int N=1e6+1000;
typedef long long ll;
int n,m,head[N];
int top[N],dfn[N],siz[N],son[N],fa[N];
int a[N],cnt,num,dep[N],b[N];
struct node{
int l,r,max;
}tr[N<<2];
struct node1{
int from;
int to;
int w;
}edge[N<<2],line[N];
void add(int from,int to,int w){
cnt++;
edge[cnt].from=head[from];
edge[cnt].to=to;
edge[cnt].w=w;
head[from]=cnt;
}
void dfs1(int now){
son[now]=-1;
siz[now]=1;
for(int i=head[now];i;i=edge[i].from){
int to=edge[i].to;
if(dep[to]) continue;
a[to]=edge[i].w;
dep[to]=dep[now]+1;
fa[to]=now;
dfs1(to);
siz[now]+=siz[to];
if(son[now]==-1||siz[to]>siz[son[now]]) son[now]=to;
}
}
void dfs2(int now,int tp){
top[now]=tp;
num++;
b[num]=a[now];
dfn[now]=num;
if(son[now]==-1) return;
dfs2(son[now],tp);
for(int i=head[now];i;i=edge[i].from){
int to=edge[i].to;
if(to!=fa[now]&&to!=son[now]) dfs2(to,to);
}
}
void build(int id,int l,int r){
tr[id].l=l;
tr[id].r=r;
if(l==r){
tr[id].max=b[l];
return;
}
int mid=(l+r)/2;
build(lson,l,mid);
build(rson,mid+1,r);
tr[id].max=max(tr[lson].max,tr[rson].max);
}
void update(int id,int x,int ad){
if(tr[id].l==tr[id].r){
tr[id].max=ad;
return;
}
int mid=(tr[id].l+tr[id].r)/2;
if(x<=mid) update(lson,x,ad);
else update(rson,x,ad);
tr[id].max=max(tr[lson].max,tr[rson].max);
}
int getmax(int id,int l,int r){
if(l>tr[id].r||r<tr[id].l) return -0x7fffffff;
if(l<=tr[id].l&&tr[id].r<=r){
return tr[id].max;
}
return max(getmax(lson,l,r),getmax(rson,l,r));
}
int treemax(int x,int y){
int maxn=-0x7fffffff;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
maxn=max(maxn,getmax(1,dfn[top[x]],dfn[x]));
x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
maxn=max(maxn,getmax(1,dfn[x]+1,dfn[y]));
return maxn;
}
int main(){
string str;
int cnt1=0;
int c,from,to,w;
cin>>n;
for(int i=1;i<n;i++){
cin>>from>>to>>w;
cnt1++;
add(from,to,w);
add(to,from,w);
line[cnt1].from=from;
line[cnt1].to=to;
line[cnt1].w=w;
}
dep[1]=1;
dfs1(1);
dfs2(1,1);
build(1,1,n);
while(cin>>str&&str!="DONE"){
if(str=="QUERY"){
cin>>from>>to;
cout<<treemax(from,to)<<endl;
}
else {
cin>>from>>to;
int dian=0;
if(dep[line[from].from]>dep[line[from].to]){
dian=line[from].from;
}
else dian=line[from].to;
update(1,dfn[dian],to);
}
}
}


