树剖(不太会)
前情提要,我主要看的是这位大佬的讲解,用的是谷的代码,所以会有点奇怪

大概就是这么个意思

dfs1用来处理树的dfs序,处理出重链大小和对应的重儿子
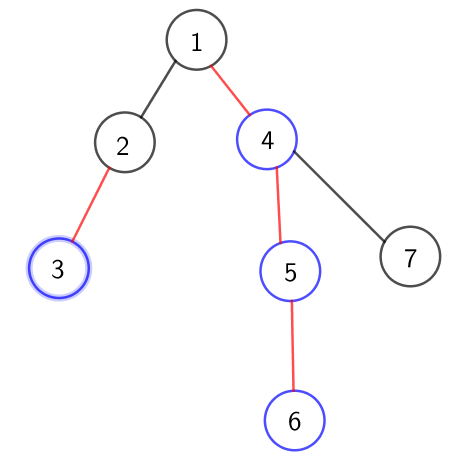
void dfs1(int now){
son[now]=-1;
siz[now]=1;
for(int i=head[now];i;i=edge[i].from){
int to=edge[i].to;
if(dep[to]) continue;//有长度说明已经算过了,正在往回走(因为建的双向边)
dep[to]=dep[now]+1;
fa[to]=now;
dfs1(to);
siz[now]+=siz[to];//加上所有子树大小得到本棵树的大小
if(son[now]==-1||siz[to]>siz[son[now]]) son[now]=to;//递归回来时已经求出了各个子树的长度,要进行比较,找出重儿子
}
}
dfs2用来处理重链的头top,以及将树重新编号dfn,使其符合一条重链上编号连续的状态,这样我们就可以在树上实现类似线段树的区间修改操作
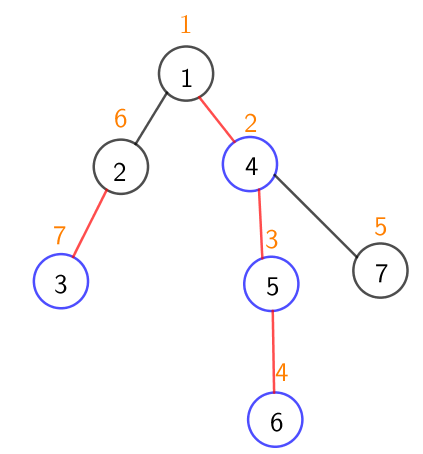
void dfs2(int now,int tp){
top[now]=tp;//tp为重链的头(不属于重儿子)
num++;
b[num]=a[now];
// pre[num]=now; 这个没必要,可以被上一行的替代
dfn[now]=num;//先跑重链,确保其连续
if(son[now]==-1) return;
dfs2(son[now],tp);
for(int i=head[now];i;i=edge[i].from){
int to=edge[i].to;
if(to!=son[now]&&to!=fa[now]) dfs2(to,to);//重链跑完后跑轻链
}
}
看代码可知,重链上的编号一定是连续的(因为是沿着重儿子跑的),递归完后跑轻链,找出轻链中剩余的重链(如图中的点3)
然后是路径求和treesum
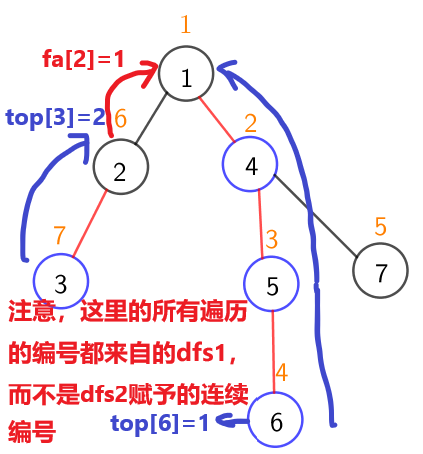
带图就好理解多了,假设我要求3到6路径上的和,那么我先将3所处的重链和6所处的重链的和求出来,利用dfs2的连续标记和线段树可以快速求和,然后6跳到1上,3跳到2的父亲1上,然后3和6就在同一重链上,这样我们直接利用两点所处重链的连续标记再次利用线段树求和
int treesum(int x,int y){
int ans=0;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
ans+=query(1,dfn[top[x]],dfn[x]);
x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
ans+=query(1,dfn[x],dfn[y]);
return ans;
}
然后没了,实际上仔细分析还是能分析出来的
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define lson id<<1
#define rson id<<1|1
const int N=1e5+10;
int n,m,r,mod;
int a[N],b[N];
struct node{
int from;
int to;
}edge[N<<2];
int head[N],num,cnt;
int fa[N],dep[N],top[N],son[N],dfn[N],idx[N],siz[N];
struct node1{
int l,r,cnt,lazy,sum;
}tr[N<<2];
void pushup(int id){
if(!tr[id].lazy) return;
tr[lson].lazy=(tr[lson].lazy+tr[id].lazy)%mod;
tr[rson].lazy=(tr[rson].lazy+tr[id].lazy)%mod;
tr[lson].sum=(tr[lson].sum+tr[id].lazy*tr[lson].cnt)%mod;
tr[rson].sum=(tr[rson].sum+tr[id].lazy*tr[rson].cnt)%mod;
tr[id].lazy=0;
}
void build(int id,int l,int r){
tr[id].l=l;
tr[id].r=r;
tr[id].cnt=r-l+1;
if(l==r){
tr[id].sum=a[l]%mod;
return;
}
int mid=(l+r)/2;
build(lson,l,mid);
build(rson,mid+1,r);
tr[id].sum=(tr[lson].sum+tr[rson].sum)%mod;
}
void update(int id,int l,int r,int ad){
if(l>tr[id].r||r<tr[id].l) return;
if(l<=tr[id].l&&tr[id].r<=r) {
tr[id].sum=(ad*tr[id].cnt+tr[id].sum)%mod;
tr[id].lazy=(tr[id].lazy+ad)%mod;
return;
}
pushup(id);
// int mid=(tr[id].l+tr[id].r)/2;
update(lson,l,r,ad);
update(rson,l,r,ad);
tr[id].sum=(tr[lson].sum+tr[rson].sum)%mod;
}
int getsum(int id,int l,int r){
if(l>tr[id].r||r<tr[id].l) return 0;
if(l<=tr[id].l&&tr[id].r<=r) {
return tr[id].sum%mod;
}
pushup(id);
// int mid=(tr[id].l+tr[id].r)/2;
return getsum(lson,l,r)+getsum(rson,l,r);
}
void add(int from,int to){
cnt++;
edge[cnt].from=head[from];
edge[cnt].to=to;
head[from]=cnt;
}
void dfs1(int x){
son[x]=-1;
siz[x]=1;
for(int i=head[x];i;i=edge[i].from){
int to=edge[i].to;
if(dep[to]) continue;
dep[to]=dep[x]+1;
fa[to]=x;
dfs1(to);
siz[x]+=siz[to];
if(son[x]==-1||siz[to]>siz[son[x]]) son[x]=to;
}
}
void dfs2(int x,int tp){
top[x]=tp;
num++;
idx[num]=x;
dfn[x]=num;
a[num]=b[x];
if(son[x]==-1) return;
dfs2(son[x],tp);
for(int i=head[x];i;i=edge[i].from){
int to=edge[i].to;
if(to!=son[x]&&to!=fa[x]) dfs2(to,to);
}
}
void addtree(int x,int y,int ad){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
update(1,dfn[top[x]],dfn[x],ad);
x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
update(1,dfn[x],dfn[y],ad);
}
int treesum(int x,int y){
int ans=0;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
ans=(ans+getsum(1,dfn[top[x]],dfn[x]))%mod;
x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
ans=(ans+getsum(1,dfn[x],dfn[y]))%mod;
return ans;
}
int main(){
int c,from,to,w;
cin>>n>>m>>r>>mod;
for(int i=1;i<=n;i++) cin>>b[i];
for(int i=1;i<n;i++){
cin>>from>>to;
add(from,to);
add(to,from);
}
dep[r]=1;
dfs1(r);
dfs2(r,r);
build(1,1,num);
for(int i=1;i<=m;i++){
cin>>c;
if(c==1){
cin>>from>>to>>w;
addtree(from,to,w);
}
else if(c==2){
cin>>from>>to;
cout<<treesum(from,to)%mod<<endl;
}
else if(c==3){
cin>>from>>w;
update(1,dfn[from],dfn[from]+siz[from]-1,w);
}
else{
cin>>from;
cout<<getsum(1,dfn[from],dfn[from]+siz[from]-1)%mod<<endl;
}
}
}
注意一点,在正常的update下要用对应的dfn值
if(str=="CHANGE"){
cin>>root>>w;
update(1,dfn[root],w);
}//对的
if(str=="CHANGE"){
cin>>root>>w;
update(1,root,w);
}//错的
还有一点,由于dfs一条路走到黑的特性,dfs2中树的编号一定均为dfn[root]到dfn[root]+siz[root]-1(减一是因为左边界包含了dfn[root],树的总大小为siz[root]),因此直接update这些编号即可
关于根的选择:
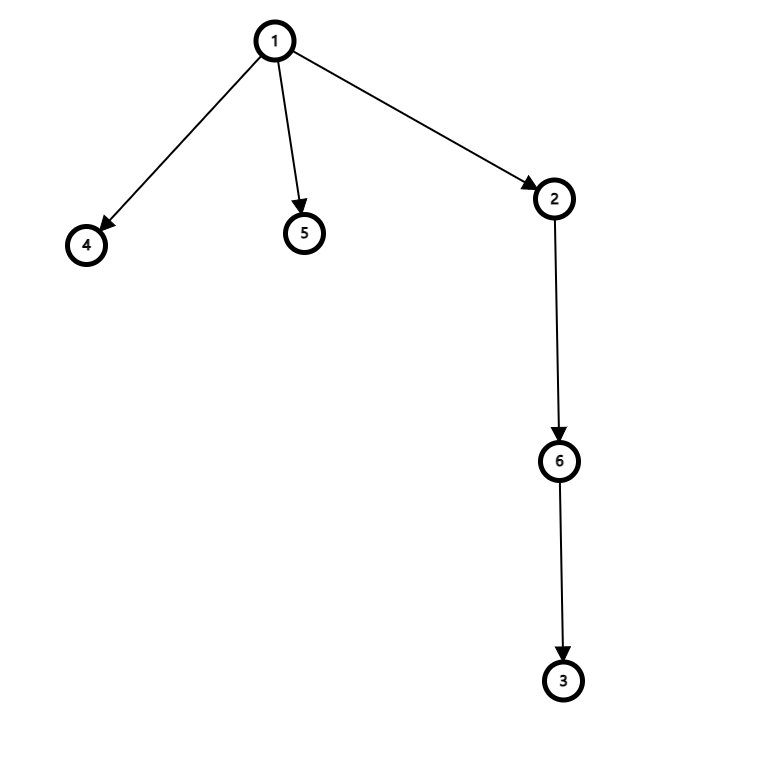
由于是单向边,一个树的根不一定为1,对此我们可以将1强行提上来,使它成为树根
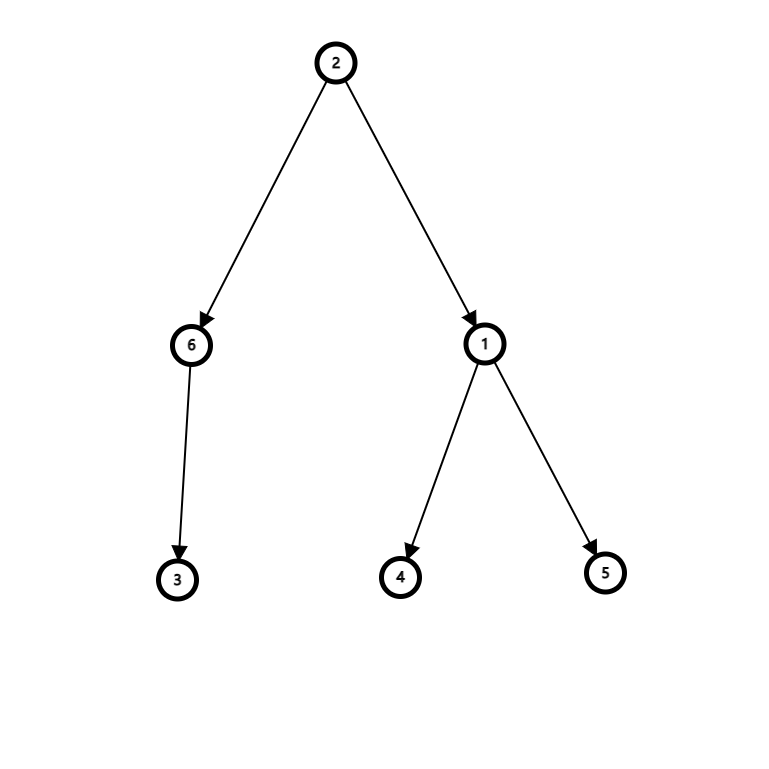
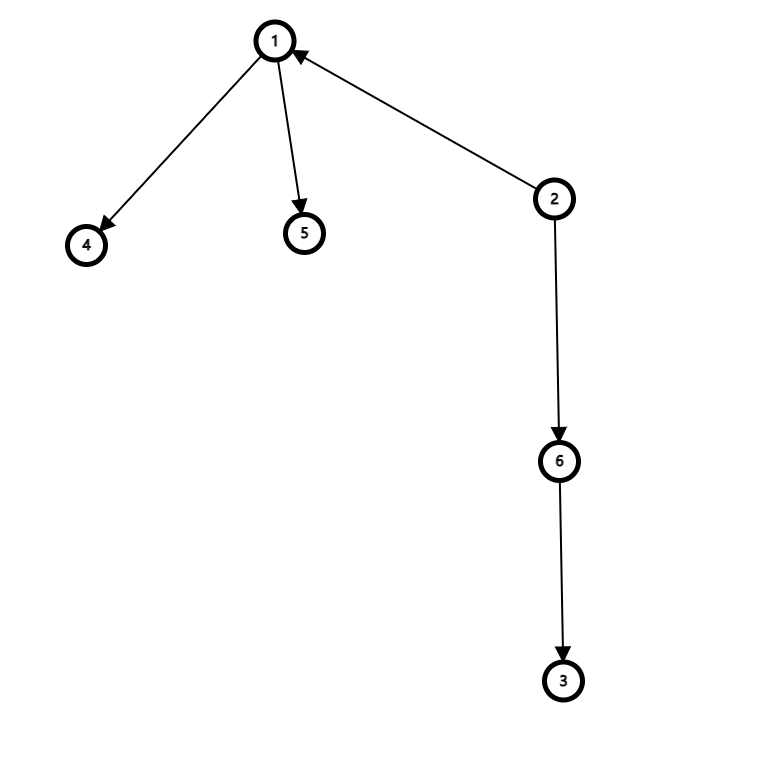
但会有一个问题,可能没有往下遍历的边(例如图中的1,2),因此要建双向边,使其成为一个无向图
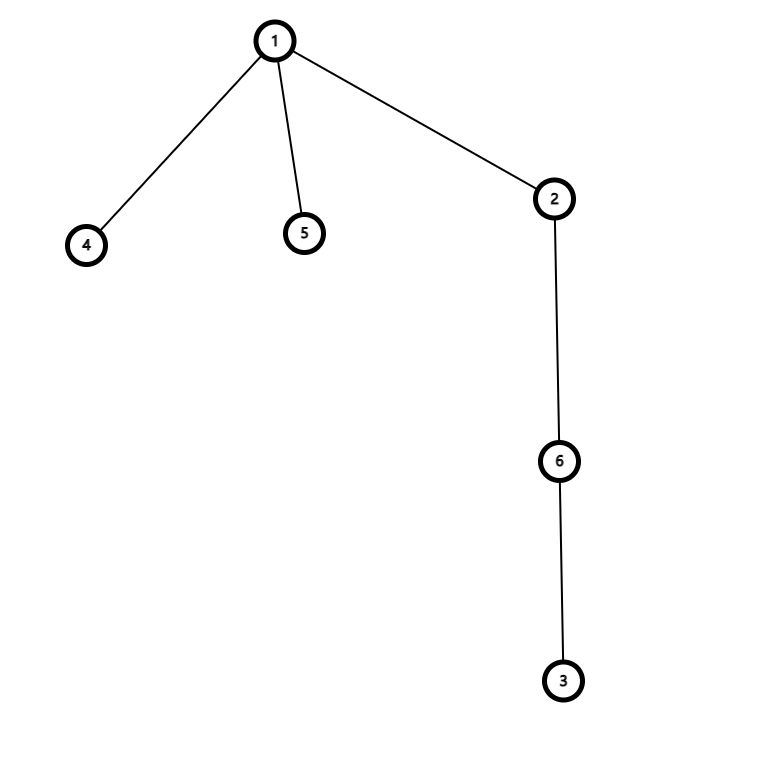
然后在往下遍历时及时return掉返回去的边
void dfs1(int now){
son[now]=-1;
siz[now]=1;
for(int i=head[now];i;i=edge[i].from){
int to=edge[i].to;
if(dep[to]) continue;//有数值说明走过了,在往回走,要及时return掉
a[to]=edge[i].w;
dian[edge[i].id]=to;
dep[to]=dep[now]+1;
fa[to]=now;
dfs1(to);
siz[now]+=siz[to];
if(son[now]==-1||siz[to]>siz[son[now]]) son[now]=to;
}
}
这样又成了一个单向图