KMP

先贴代码

点击查看代码

	int j=0;
	for(int i=2;i<=len2;i++)
	{
		while(j&&s2[j+1]!=s2[i]) j=nxt[j];
		if(s2[j+1]==s2[i]) j=j+1;
		nxt[i]=j;
	}//自己匹配
	
	j=0;
	for(int i=1;i<=len1;i++)
	{
		stk[++top]=i;
		while(j&&s2[j+1]!=s1[i]) j=nxt[j];
		if(s2[j+1]==s1[i]) j=j+1;
	}//与别人匹配

点击查看代码

#include<bits/stdc++.h>
using namespace std;
char s1[120000];
int nex[120000];
int n,m;
char s2[120000];
int len1;
void nx(char str[]){
	int j=0;
	for(int i=2;i<=len1;i++){
		while(j&&str[j+1]!=str[i]) j=nex[j];
		if(str[j+1]==str[i]) j++;
		nex[i]=j;
	}
}
int kmp(char str[]){
	int len=strlen(str+1),j=0;
	for(int i=1;i<=len;i++){
		while(j&&s1[j+1]!=str[i]) j=nex[j];
		if(s1[j+1]==str[i]) j++;
		if(j==len1) return 1;
	}
	return 0;
}
int main(){
	scanf("%s",s1+1);
	len1=strlen(s1+1);
	nx(s1);
	cin>>n;
	for(int i=1;i<=n;i++){
		memset(s2,0,sizeof(s2));
		scanf("%s",s2+1);
		if(kmp(s2)) cout<<"YES"<<endl;
		else cout<<"NO"<<endl;
	}
}
/*
输出结果如下
aaaaa
4
aaa
NO
aaaaaaa
YES
abdc
NO
aaaaaabcd
YES
*/

复活！
kmp算法的核心思想就是：对于某个位置不匹配的字符，将结合之前储存的信息，直接跳到下一个能够开始匹配的子串

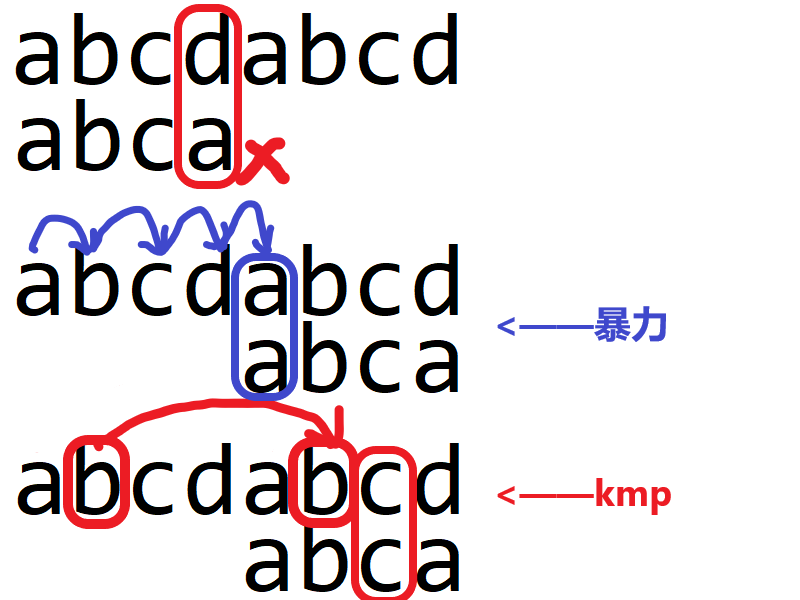
逐步分析一下代码
首先理解几个概念
1.nex（next）数组是存储前i个字符前缀和后缀相等的最大长度（不包含i长度），例如aaaaa的next[5]=4，而不是5;

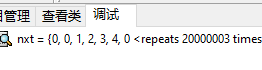
2.进行自我匹配的是要去匹配主串的子串
3.我写的代码是从下标为一的字符串开始的,会有不同
4.next[1]=0,所以可以直接从二开始

int j=0;
for(int i=2;i<=len2;i++)

首先 j=0比较好理解，因为还没有匹配得上的字符，所以为零(可以类比状压的预处理为什么从零开始而不是一)，i=2上面解释过了，因为next[1]=0,

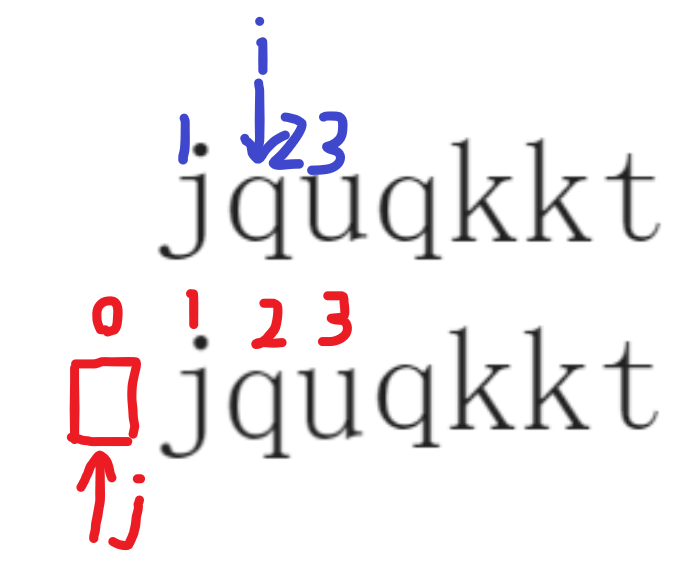
while(j&&s2[j+1]!=s2[i]) j=nxt[j];

接着，判断j是因为可能还没有匹配的上的字符，所以要先跳过并拉去匹配，s[j+1]!=s[i]就是不断的将j往前推,直到没有匹配(j=0)或s2[j+1]= =s2[i],最终匹配完然后就是next[i]=j,但有以下几个问题：
1.为什么是j+1和i匹配：
j是从上一次循环中继承过来的，也就是说，实际上是s[j]= =s[i-1]，即s[j+1]= =s[i]
2.匹配不成功为什么是j=next[j]
因为当前 前后缀匹配的最大长度肯定是从前面已经成功匹配的状态转移过来的（仅需要对符合条件的状态+1就是当前的最大长度），又因为j一定大于next[j]（且next[j]和j均为已经成功匹配的状态），所以这实际上相当于一个去求最大长度的倒序的dp
3.为什么while完还需判断(因为在这个长度下可能真的一点都不匹配)

然后就是与主串的匹配了

for(int i=1;i<=len1;i++)//这就不用说了吧
while(j&&s2[j+1]!=s1[i]) j=nex[j];//s2是要去匹配的，s1是主串

开始分析

实际上也很好想（不好想）
我们为什么要求前后缀，以上图为例，看上图中圈出来的AB，有没有发现什么？我们在匹配中就已经得知了后面主串中还有一个AB（主串中第二个AB）与子串的前两个字符（AB）对应，而它们对应的下标，刚好就是求出的最大长度，所以很明显，在匹配不成功时，我可以直接从子串AB的下标j+1与后面i接着匹配，而不用再去重新从j=0开始匹配，这便是kmp的精髓