[Tarjan] 矿场搭建 题解
题目描述
煤矿工地可以看成是由隧道连接挖煤点组成的无向图。为安全起见,希望在工地发生事故时所有挖煤点的工人都能有一条出路逃到救援出口处。于是矿主决定在某些挖煤点设立救援出口,使得无论哪一个挖煤点坍塌之后,其他挖煤点的工人都有一条道路通向救援出口。
请写一个程序,用来计算至少需要设置几个救援出口,以及不同最少救援出口的设置方案总数。
输入格式

输出格式
输入文件中有多少组数据,输出文件中就有多少行。每行对应一组输入数据的结果。
其中第 i 行以 Case i: 开始(注意大小写,Case 与 i 之间有空格,i 与 : 之间无空格,: 之后有空格),其后是用空格隔开的两个正整数,第一个正整数表示对于第 组输入数据至少需要设置几个救援出口,第二个正整数表示对于第 组输入数据不同最少救援出口的设置方案总数。
输出格式参照以下输入输出样例。
样例
样例输入
9
1 3
4 1
3 5
1 2
2 6
1 5
6 3
1 6
3 2
6
1 2
1 3
2 4
2 5
3 6
3 7
0
样例输出
Case 1: 2 4
Case 2: 4 1

题解
这是一张无向图,我们可以发现,对于它的一个子图D,如果D中任意两点都联通,那么我们就可以将D缩成一个点,然后在进行操作,这不就是Tarjan求点双连通分量吗;
求完以后,很显然,点双的个数就是我们要找的最少出口个数(这里不再过多进行解释);
对于第二问,应该如何处理呢?
我们知道,每个D中可能会有0,1,2...个对于整张图的割点(点双性质),对于这几种情况,我们可以分别讨论;
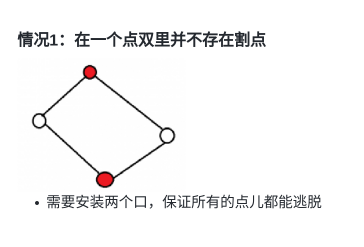
- 当割点个数为0时,很显然,整张图是点双,可以得出最少出口个数为2(因为当一个出口塌了的时候,还可以从另一个出去),方案数为m * (m - 1) >> 1(其中m为点数,从m个点中选两个,用排列即可解决);
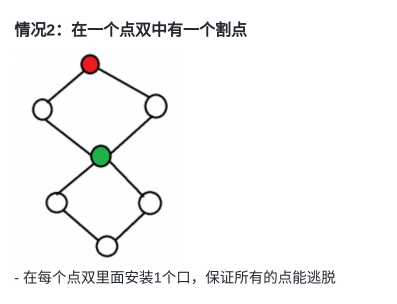
- 当割点个数为1时,我们只需在每个D中建一个不是割点的出口即可;
证明:当割点塌了时,可以从D中的出口出;当出口塌了时,可以从割点去其他的D中出
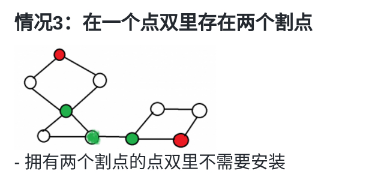
- 当割点个数>1时,不用设出口,因为从D中可以去至少2个其它的D出去;
上述图片转载自https://www.cnblogs.com/Charlieljk/p/17888945.html
如果还是看不懂,去搜搜Tarjan求点双;
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <stack>
#include <vector>
#include <algorithm>
using namespace std;
int n, m;
struct sss{
int t, ne;
}e[500005];
int h[500005], cnt;
void add(int u, int v) {
e[++cnt].ne = h[u];
h[u] = cnt;
e[cnt].t = v;
}
int dfn[500005], low[500005];
int num;
stack<int> s;
vector<int> ds[500005];
vector<int> a;
bool cd[500005];
int dcnt;
void tarjan(int x, int root, int fa) { //Tarjan求点双联通分量;
dfn[x] = low[x] = ++num;
s.push(x);
int son = 0;
bool first = true;
for (int i = h[x]; i; i = e[i].ne) {
int u = e[i].t;
if (first && u == fa) {
first = false;
continue;
}
if (!dfn[u]) {
son++;
tarjan(u, root, x);
low[x] = min(low[x], low[u]);
if (low[u] >= dfn[x]) {
if (x != root || son > 1) {
cd[x] = true;
}
dcnt++;
ds[dcnt].push_back(x);
int t = 0;
do {
t = s.top();
s.pop();
ds[dcnt].push_back(t);
} while(t != u);
}
} else {
low[x] = min(low[x], dfn[u]);
}
}
return;
}
int main() {
scanf("%d", &n);
int ssum = 0;
while(n) {
int x, y;
ssum++;
memset(dfn, 0, sizeof(dfn));
memset(low, 0, sizeof(low));
cnt = 0;
num = 0;
dcnt = 0;
long long ans = 0;
long long an = 1;
memset(h, 0, sizeof(h));
memset(e, 0, sizeof(e));
memset(cd, 0, sizeof(cd));
memset(ds, 0, sizeof(ds));
a.clear();
while(!s.empty()) s.pop();
for (int i = 1; i <= n; i++) {
scanf("%d %d", &x, &y);
add(x, y);
add(y, x);
a.push_back(x);
a.push_back(y);
}
sort(a.begin(), a.end());
m = unique(a.begin(), a.end()) - a.begin(); //m为点数;
for (int i = 1; i <= m; i++) {
if (!dfn[i]) tarjan(i, i, i);
}
for (int i = 1; i <= dcnt; i++) {
int c = 0;
for (int j = 0; j < ds[i].size(); j++) {
if (cd[ds[i][j]]) c++;
}
if (c == 1) {
ans++;
an *= (ds[i].size() - 1);
}
}
if (ds[1].size() == m) { //整张图是点双;
ans = 2;
an = ds[1].size() * (ds[1].size() - 1) >> 1;
}
printf("Case %d: %lld %lld\n", ssum, ans, an);
scanf("%d", &n);
}
return 0;
}


