[树形DP] 选课 题解
题目描述
大学里实行学分。每门课程都有一定的学分,学生只要选修了这门课并考核通过就能获得相应的学分。学生最后的学分是他选修的各门课的学分的总和。
每个学生都要选择规定数量的课程。其中有些课程可以直接选修,有些课程需要一定的基础知识,必须在选了其它的一些课程的基础上才能选修。 例如,《数据结构》必须在选修了《高级语言程序设计》之后才能选修。我们称《高级语言程序设计》是《数据结构》的先修课。 每门课的直接先修课最多只有一门。两门课也可能存在相同的先修课。为便于表述每门课都有一个课号,课号依次为1,2,3,……。 下面举例说明:
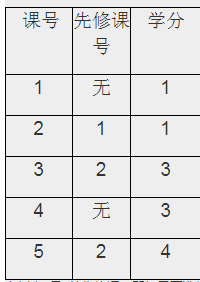
上例中1是2的先修课,即如果要选修2,则1必定已被选过。同样,如果要选修3,那么1和2都一定已被选修过。
学生不可能学完大学所开设的所有课程,因此必须在入学时选定自己要学的课程。每个学生可选课程的总数是给定的。现在请你找出一种选课方案,使得你能得到学分最多,并且必须满足先修课优先的原则。假定课程之间不存在时间上的冲突。
输入格式
输入文件的第一行包括两个正整数M、N(中间用一个空格隔开)其中M表示待选课程总数(1≤M≤1000),N表示学生可以选的课程总数(1≤N≤M)。
以下M行每行代表一门课,课号依次为1,2……M。每行有两个数(用一个空格隔开),第一个数为这门课的先修课的课号(若不存在先修课则该项为0),第二个数为这门课的学分。学分是不超过10的正整数。
输出格式
输出文件第一行只有一个数,即实际所选课程的学分总数。
样例
样例输入
7 4
2 2
0 1
0 4
2 1
7 1
7 6
2 2
样例输出
13
题解
不难看出,这道题的数据结构是树,对于某些课程,选它就必选其它某一门课程,并且根节点的最优解可以由子树转移而来,再看看数据范围,这不就是有依赖的背包DP--树形背包吗;
我们采用性能比较中庸的链式前向星存图,让每一个被依赖的指向依赖的(即父亲指向儿子),发现会存出一个森林,为了我们使用树形DP,可以模拟一个虚点0来连接每个根,这样就得到了一棵树;
下面就开始DP,由于树本身的DFS性,我们用DFS的形式来DP;
首先考虑状态设计,定义f[i][j][k]表示以i为根的前j棵子树,选了k门课程的最大学分;
按背包DP的思想考虑,f[i][j][k] 应由f[i][j - 1][k - u] + f[v][vv][u] 转移而来;其中,u为选的课程数,需要枚举,v是i的一个子树(j以后的),vv代表v的子树总个数;
所以---
状态转移方程
剩下就是初始化了,很容易想到,不管选哪棵子树,f[x][1 ~ x的子树总个数][1] = 选x这门课的学分;
OK,你可以开始写了;
但作为追求卓越的先锋,三维仍然是有些冗余;
考虑优化;
想到01背包二维转化成一维的优化(滚动数组),我们也可以借鉴一下,将第二维优化掉,改成倒序循环;
定义f[i][j]表示以i为根,选了j门课程的最大学分;
于是---
新的状态转移方程
其中,v为i的子树,k需要枚举;
初始化:f[x][1] = 选x这门课的学分;
代码
#include <iostream>
#include <cstring>
using namespace std;
int n, m;
int f[1005][1005];
int a[1005];
struct sss{
int t, ne;
}e[10005];
int h[10005], cnt;
void add(int u, int v) {
e[++cnt].t = v;
e[cnt].ne = h[u];
h[u] = cnt;
}
int dfs(int x) {
int p = 1; //子树的课程总个数,最小是叶子节点1;
f[x][1] = a[x]; //初始化;
for (int i = h[x]; i != -1; i = e[i].ne) {
int s = dfs(e[i].t);
for (int j = p; j; j--) { //j循环根节点课程个数,对于本阶段是p(总个数);
for (int k = 1; k + j <= m + 1 && k <= s; k++) { //k循环子树课程个数,上限是s,同时要满足k + j <= m + 1;
f[x][j + k] = max(f[x][j + k], f[x][j] + f[e[i].t][k]);
}
}
p += s; //将每次DFS的子树的课程个数累加;
}
return p; //返回课程个数;
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) {
e[i].ne = 0;
e[i].t = 0;
}
memset(h, -1, sizeof(h));
memset(f, 0, sizeof(f));
memset(a, 0, sizeof(a));
cnt = 0;
int b;
for (int i = 1; i <= n; i++) {
cin >> b >> a[i];
add(b, i);
}
dfs(0);
cout << f[0][m + 1] << endl; //最多选m + 1门课,因为还有虚点
cin >> n >> m;
return 0;
}


