[数据结构] [算法] [PEP总结] C++信奥常用模板总结

杂项模板

快读快写（__int128适用）

点击查看代码 
#include <iostream>
using namespace std;
typedef __int128 LLL;
LLL read() {
    LLL x = 0, f = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9') {
        if (ch == '-') f = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') {
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}

void out(LLL x) {
    if (x < 0) putchar('-'), x = -x;
    if (x > 9) out(x / 10);
    putchar(x % 10 + '0');
}
int n;
int main() {
	cin >> n;
	__int128 a, b;
	char c;
	for (int i = 1; i <= n; i++) {
		a = read();
		cin >> c;
		b = read();
		if (c == '+') {
			out(a + b);
			cout << endl;
		}
		if (c == '-') {
			out(a - b);
			cout << endl;
		}
	}
	return 0;
}

筛法求素数

点击查看代码 
//埃氏筛 O(n log log n); 

#include <iostream>
#include <cstring>
using namespace std;
int n;
int vis[100000005];
int main() {
	cin >> n;
	memset(vis, 0, sizeof(vis));
	for (int i = 2; i <= n; i++) {
		if (vis[i]) continue;
		cout << i << endl;
		for (int j = i; j <= n / i; j++) vis[i * j] = 1;
	}
	return 0;
}

//线性筛 O(n);

#include <iostream>
#include <cstdio>
using namespace std;
int pri[100000005], cnt;
bool vis[100000005];
void w(int x) {
	for (int i = 2; i <= x; i++) {
		if (!vis[i]) pri[++cnt] = i;
		for (int j = 1; j <= cnt && i * pri[j] <= x; j++) {
			vis[i * pri[j]] = true;
			if (i % pri[j] == 0) break;
		}
	}
	cout << cnt << endl;
	for (int i = 1; i <= cnt; i++) cout << pri[i] << ' ';
}
int main() {
	freopen("in.in", "r", stdin);
	freopen("out.out", "w", stdout);
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	w(100000000);
	return 0;
}

高精度

点击查看代码 
#include <iostream>
#include <string>
#include <cstring>
using namespace std;
char a[10005], b[10005];
int a1[10005], b1[10005], c[10005];
int lena, lenb, lenc;
int x; //进位；
void gao_jing_jia(int a1[], int b1[]) {
	memset(c, 0, sizeof(c));
	lenc = max(lena, lenb);
	x = 0;
	for (int i = 0; i <= lenc - 1; i++) {
		c[i] = a1[i] + b1[i] + x;
		x = c[i] / 10;
		c[i] %= 10;
	}
	if (x) {
		lenc++;
		c[lenc - 1] = x;
	}
}
void gao_jing_jian(int a1[], int b1[]) {
	memset(c, 0, sizeof(c));
	lenc = max(lena, lenb);
	x = 0;
	if ((lena < lenb) || ((lena == lenb) && a1[lena - 1] < b1[lenb - 1])) {
		cout << '-';
		for (int i = 0; i <= lenc - 1; i++) {
			if (b1[i] - a1[i] < 0) {
				b1[i + 1]--;
				b1[i] += 10;
			}
			c[i] = b1[i] - a1[i];
		}
		while(!c[lenc - 1]) {
			if (lenc - 1 == 0) break;
			lenc--;
		}
	} else {
		for (int i = 0; i <= lenc - 1; i++) {
			if (a1[i] - b1[i] < 0) {
				a1[i + 1]--;
				a1[i] += 10;
			}
			c[i] = a1[i] - b1[i];
		}
		while(!c[lenc - 1]) {
			if (lenc - 1 == 0) break;
			lenc--;
		}
	}
}
void gao_jing_cheng(int a1[], int b1[]) {
	if (((lena == 1) && a1[0] == 0) || ((lenb == 1) && b1[0] == 0)) {
		c[0] = 0;
		lenc = 1;
		return;
	}
	lenc = lena + lenb;
	for (int i = 0; i <= lena - 1; i++) {
		for (int j = 0; j <= lenb - 1; j++) {
			c[i + j] += a1[i] * b1[j];
			c[i + j + 1] += c[i + j] / 10;
			c[i + j] %= 10;
		}
	}
	while(!c[lenc - 1]) lenc--;
}
int main() {
	cin >> a >> b;
	lena = strlen(a);
	lenb = strlen(b);
	for (int i = 0; i < lena; i++) { //倒着存，方便进位； 
		a1[i] = a[lena - i - 1] - '0';
	}
	for (int i = 0; i < lenb; i++) {
		b1[i] = b[lenb - i - 1] - '0';
	}
//	gao_jing_jia(a1, b1);
//	gao_jing_jian(a1, b1);
//	gao_jing_cheng(a1, b1);
	for (int i = lenc - 1; i >= 0; i--) {
		cout << c[i];
	}
	return 0;
}

归并排序与逆序对

点击查看代码 
#include <iostream>
#include <cstdio>
using namespace std;
int a[5000005]; //待排序数组；
int r1[5000005]; //排好序数组；
int n;
long long ans; //注意long long；
void merge_sort(int l, int r) {
	if (l == r) return;
	int m = (l + r) >> 1;
	int i, j, k;
	merge_sort(l, m);
	merge_sort(m + 1, r);
	i = l;
	k = l;
	j = m + 1;
	while(i <= m && j <= r) {
		if (a[i] <= a[j]) { //注意等号，会影响下面的逆序对个数；
			r1[k] = a[i]; //r[k]每次都存较小的那一个；
			k++;
			i++;
		}
		if (a[i] > a[j]) {
			r1[k] = a[j];
			k++;
			j++;
			ans += m - i + 1; //逆序对个数，因为r数组已部分排好序（从中点出发），所以m - i + 1就是逆序对个数；
		}
	}
	while(i <= m) { //将左边剩余元素接入r数组中；
		r1[k] = a[i];
		i++;
		k++;
	}
	while(j <= r) { //将右边剩余元素接入r数组中；
		r1[k] = a[j];
		j++;
		k++;
	}
	for (int i = l; i <= r; i++) {
		a[i] = r1[i]; //将a数组排为有序；
	}
}
int main() {
	scanf("%d", &n); //不要用cin，否则可能会超时；
	for (int i = 1; i <= n; i++) {
		scanf("%d", &a[i]);
	}
	merge_sort(1, n);
	for (int i = 1; i <= n; i++) {
		cout << a[i] << ' ';
	}
	printf("\n");
	printf("%lld", ans);
	return 0;
}

二分查找与二分答案

点击查看代码 
#include <iostream>
using namespace std;
int a[10005];
int n;
int l, r;
int y;
bool check(int x) {
	if (a[x] >= y) return true;
	else return false;
}
int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	cin >> y; //待查找元素； 
	l = 1;
	r = n;
	while(l <= r) {
		int mid = (l + r) >> 1;
		if (check(mid)) {
			r = mid - 1;
		} else {
			l = mid + 1;
		}
	}
	if (a[l] != y) {
		cout << "No Answer!";
		return 0;
	}
	cout << l;
	return 0;
}

快速幂取模

输出 $ a^b \mod c $ 的值；

点击查看代码 
#include <iostream>
using namespace std;
long long a, b, c;
long long kuai_su_mi(long long a, long long b, long long c) {
	long long ans = 1;
	while (b > 0) {
		if (b & 1) {
			ans = (ans * a) % c;
		}
		a = a * a % c;
		b >>= 1;
	}
	return ans;
}
int main() {
	cin >> a >> b >> c;
	cout << kuai_su_mi(a, b, c);
	return 0;
}

图论模板

<1> 树基础

二叉树的前，中，后序遍历

点击查看代码 
#include <iostream>
using namespace std;
int n;
struct sss{ //树的存储；
	char v;
	int ls, rs; //节点值，左孩子（编号），右孩子（编号）；
}tr[100005];
void xian(int x) { //根左右；
	if (x != 0) {
		cout << tr[x].v;
		xian(tr[x].ls);
		xian(tr[x].rs);
	}
}
void zhong(int x) { //左根右；
	if (x != 0) {
		zhong(tr[x].ls);
		cout << tr[x].v;
		zhong(tr[x].rs);
	}
}
void hou(int x) { //左右根；
	if (x != 0) {
		hou(tr[x].ls);
		hou(tr[x].rs);
		cout << tr[x].v;
	}
}
int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> tr[i].v;
		cin >> tr[i].ls >> tr[i].rs;
	}
	xian(1);
	cout << endl;
	zhong(1);
	cout << endl;
	hou(1);
	cout << endl;
	return 0;
}

普通树转二叉树

点击查看代码 
#include <iostream>
using namespace std;
int n;
struct sss{
	char a;
	int ls, rs;
}e[100005];
void qian(int x) {
	if (x) {
		cout << e[x].a;
		qian(e[x].ls);
		qian(e[x].rs);
	}
}
void hou(int x) {
	if (x) {
		hou(e[x].ls);
		hou(e[x].rs);
		cout << e[x].a;
	}
}
int main() {
	cin >> n;
	int o = 1;
	int b;
	int p;
	for (int i = 1; i <= n; i++) {
		cin >> e[i].a;
		cin >> b;
		if (b != 0) {
			e[i].ls = b; //将与根节点链接的第一个节点作为此节点的左孩子； 
		}
		p = b;
		while (b != 0) {
			cin >> b;
			if (b != 0) { //有可能b == 0，所以要特判； 
				e[p].rs = b; //加边，原来的兄弟变为右孩子； （同时也删了边（兄弟和根节点的边））； 
			}
			p = b;
		}
	}
	qian(1);
	cout << endl;
	hou(1);
	return 0;
} //最后旋转处理（在纸上）就可得到一个二叉树；

已知中后求前

点击查看代码 
#include <iostream>
#include <string>
using namespace std;
string a, b;
void zhong_hou_qiou_qian(string x, string y) {
	int xl = x.size(), yl = y.size();
	cout << y[yl - 1];
	if (yl == 1) return; //只有根节点；
	int k = x.find(y[yl - 1], 0);
	if (k > 0) {
		string s1 = x.substr(0, k);
		string s2 = y.substr(0, k);
		zhong_hou_qiou_qian(s1, s2);
	}
	if (k < yl - 1) {
		string s3 = x.substr(k + 1, xl - k - 1);
		string s4 = y.substr(yl - s3.size() - 1, s3.size());
		zhong_hou_qiou_qian(s3, s4);
	}
}
int main() {
	cin >> a >> b;
	zhong_hou_qiou_qian(a, b);
	return 0;
}

已知前中求后

点击查看代码 
#include <iostream>
#include <string>
using namespace std;
string a, b;
int s;
void qian_zhong_qiou_hou(int l, int r) {
	if (l > r) return; //当l == r时还能再找根（下标为l）；不能写l >= r； 
	for (int i = l; i <= r; i++) {
		if (a[s] == b[i]) { //如果在b中找到根； 
			s++; //更新根； 
			qian_zhong_qiou_hou(l, i - 1);
			qian_zhong_qiou_hou(i + 1, r); //递归时不能再有此根； 
			cout << b[i]; //左右根； 
		}
	}
} 
int main() {
	cin >> a >> b;
	s = 0;
	qian_zhong_qiou_hou(0, a.size() - 1);
	return 0;
}

注：已知前后不能求中，因为树不是唯一确定的；

二叉排序树（中序遍历有序）

左子树的所有节点比此节点小，右子树的所有节点比此节点大

点击查看代码 
板子（无注释）：
#include <iostream>
using namespace std;
struct sss{
	int a;
	int ls, rs;
}e[1000005];
int n;
void zhong(int x) {
	if (x) {
		zhong(e[x].ls);
		cout << e[x].a << ' ';
		zhong(e[x].rs);
	}
}
void hou(int x) {
	if (x) {
		hou(e[x].ls);
		hou(e[x].rs);
		cout << e[x].a << ' ';
	}
}
int main() {
	cin >> n;
	int x = 0;
	int p = 0;
	for (int i = 1; i <= n; i++) {
		cin >> e[i].a;
		x = e[i].a;
		if (i == 1) continue;
		p = 1;
		while(1) {
			if (x < e[p].a) {
				if (e[p].ls != 0) {
					p = e[p].ls;
					continue;
				} else {
					e[p].ls = i;
					break;
				}
			} else {
				if (e[p].rs != 0) {
					p = e[p].rs;
					continue;
				} else {
					e[p].rs = i;
					break;
				}
			}
		}
	}
	zhong(1);
	cout << endl;
	hou(1);
	return 0;
}

最优二叉树（哈夫曼树 Huffman Tree）

带权路径长度之和达到最小的二叉树

点击查看代码 
板子（无注释）：

#include <iostream>
using namespace std;
long long n;
struct sss{
	long long a;
	long long ls, rs;
}e[100005];
sss eg[100005];
int k;
long long ma() {
	long long t = -1;
	for (int i = 1; i <= n; i++) {
		if (e[i].a > t) {
			t = e[i].a;
			k = i;
		}
	}
	e[k].a = -1;
	return t;
}
long long mi() {
	long long t = 0xfffffffffffff;
	for (int i = 1; i <= n; i++) {
		if (eg[i].a < t) {
			t = eg[i].a;
			k = i;
		}
	}
	eg[k].a = 0xfffffffffff;
	return t;
}
void ma_t() {
	for (int i = n + 1; i <= 2 * n - 1; i++) {
		e[i].ls = ma();
		e[i].rs = ma();
		e[i].a = e[i].ls * e[i].rs + 1;
		e[k].a = e[i].a;
	}
}
void mi_t() {
	for (int i = n + 1; i <= 2 * n - 1; i++) {
		eg[i].ls = mi();
		eg[i].rs = mi();
		eg[i].a = eg[i].ls * eg[i].rs + 1;
		eg[k].a = eg[i].a;
	}
}
int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> e[i].a;
		eg[i].a = e[i].a;
	}
	mi_t();
	ma_t();
	cout << eg[2 * n - 1].a << endl;
	cout << e[2 * n - 1].a << endl;
	cout << eg[2 * n - 1].a - e[2 * n - 1].a;
	return 0;
}

<2> 图的最短路（注意初始化）

邻接矩阵

点击查看代码 
#include <iostream>
using namespace std;
int n;
int a[1005][1005];
int main() {
	cin >> n;
	int x, y, w; //起点，终点，权值；
	for (int i = 1; i <= n; i++) {
		cin >> x >> y >> w;
		a[x][y] = w;
		a[y][x] = w; //双向边，若有向图则不用加； 
	}
	return 0;
}

链式前向星

点击查看代码 
#include <iostream>
using namespace std;
int n;
struct sss{
	int t, ne, w;
}e[100005];
int h[100005], cnt;
void add(int u, int v, int ww) {
	e[++cnt].t = v;
	e[cnt].ne = h[u];
	e[cnt].w = ww;
	h[u] = cnt;
}
int main() {
	cin >> n;
	int x, y, w; //起点，终点，权值；
	for (int i = 1; i <= n; i++) {
		cin >> x >> y >> w;
		add(x, y, w);
		add(y, x, w); //双向边，若有向图则不用加；
	}
	for (int i = 1; i <= n; i++) {
		cout << i << "连接的点";
		for (int j = h[i]; j; j = e[j].ne) {
			cout << e[j].t << ' ';
		}
		cout << endl; 
	} //遍历；
	return 0;
}

弗洛伊德（Floyd）

DP的思想，$ \Theta(n^3) $ 的做法；
多源最短路；

模板（邻接矩阵）：

点击查看代码 
#include <iostream>
#include <cstring>
using namespace std;
int n, m; //n个点，m条边； 
int a[1005][1005]; 
int main() {
	cin >> n >> m;
	memset(a, 0x3f, sizeof(a)); //后面要找min，所以初始化很大； 
	int x, y, w;
	for (int i = 1; i <= n; i++) a[i][i] = 0;
	for (int i = 1; i <= m; i++) {
		cin >> x >> y >> w;
		a[x][y] = a[y][x] = w;
	}
	for (int k = 1; k <= n; k++) { //先枚举中间点；
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= n; j++) {
				a[i][j] = min(a[i][j], a[i][k] + a[k][j]);
			}
		}
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			cout << a[i][j] << ' ';
		}
		cout << endl;
	}
	return 0;
}

Floyd求最小环

点击查看代码 
#include <iostream>
#include <cstring>
using namespace std;
int n, m; //n个点，m条边；
int a[1005][1005]; 
int dis[1005][1005];
int main() {
	cin >> n >> m;
	memset(dis, 0x3f, sizeof(dis)); //后面要找min，所以初始化很大； 
	int x, y, w;
	for (int i = 1; i <= n; i++) a[i][i] = 0;
	for (int i = 1; i <= m; i++) {
		cin >> x >> y >> w;
		a[x][y] = a[y][x] = w;
		dis[x][y] = dis[y][x] = w;
	}
	int ans = 0xfffffffffff;
	for (int k = 1; k <= n; k++) { //先枚举中间点；
		for (int i = 1; i <= k - 1; i++) {
			for (int j = i; j <= k - 1; j++) {
				ans = min(ans, dis[i][j] + a[j][k] + a[k][i]);
			}
		}
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= n; j++) {
				dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
			}
		}
	}
	cout << ans; //最小环长度； 
	return 0;
}

Dijstra

每次松弛一个点，一共松弛n次

朴素 $ O(n^2) $ 模板（邻接矩阵）；

点击查看代码 
#include <iostream>
#include <cstring>
using namespace std;
int n, m; //点数，边数；
int dis[100005];
bool vis[100005];
int a[1005][1005];
void Dijstra(int x) { //x为起点； 
	memset(dis, 0x3f, sizeof(dis));
	memset(vis, 0, sizeof(vis));
	dis[x] = 0;
	int t = -1;
	for (int i = 2; i <= n; i++) { //除去起点，只需松弛n - 1次；
		for (int j = 1; j <= n; j++) {
			if (!vis[x] && (t == -1 || dis[j] < dis[t])) t = j; //找到离源点最近的最优点； 
		}
		vis[t] = true;
		for (int j = 1; j <= n; j++) {
			if (dis[j] < dis[t] + a[t][j]) {
				dis[j] = dis[t] + a[t][j];
			}
		}
	}
	if (dis[m] == 0x3f3f3f3f) {
		cout << -1;
	} else cout << dis[m];
}
int main() {
	cin >> n >> m;
	int x, y, w;
	for (int i = 1; i <= n; i++) {
		cin >> x >> y >> w;
		a[x][y] = w;
		a[y][x] = w;
	}
	Dijstra(1);
	return 0;
}

堆优化 $ \Theta(m log m) $

点击查看代码 
#include <iostream>
#include <queue>
#include <cstring>
#include <cmath>
using namespace std;
int n, m, s; //点数，边数；
struct sss {
	int t, ne, w;
}e[10000005];
int h[10000005], cnt;
void add(int u, int v, int ww) {
	e[++cnt].w = ww;
	e[cnt].ne = h[u];
	e[cnt].t = v;
	h[u] = cnt;
}
int dis[10000005];
bool vis[10000005];
typedef pair<int, int> P;
void Dijstra_dui_you_hua(int x) {
	for (int i = 1; i <= n; i++) {
		dis[i] = pow(2, 31) - 1;
	}
	memset(vis, 0, sizeof(vis));
	dis[x] = 0;
	priority_queue<P, vector<P>, greater<P> > q; //权值在前，序号在后，队列里存的是已经松驰过的；
	q.push({0, x});
	while(!q.empty()) {
		int t = q.top().first;
		int xu = q.top().second;
		q.pop();
		if (vis[xu]) continue;
		vis[xu] = true;
		for (int i = h[xu]; i; i = e[i].ne) {
			int u = e[i].t;
			if (dis[u] > dis[xu] + e[i].w) {
				dis[u] = dis[xu] + e[i].w;
				q.push({dis[u], u});
			}
		}
	}
}
int main() {
	freopen("in.in", "r", stdin);
	freopen("out.out", "w", stdout);
	cin >> n >> m >> s;
	int x, y, w;
	for (int i = 1; i <= m; i++) {
		cin >> x >> y >> w;
		add(x, y, w);
	}
	Dijstra_dui_you_hua(s);
	for (int i = 1; i <= n; i++) {
		cout << dis[i] << ' ';
	}
	return 0;
}

拓扑排序求最长路

应用范围：有向无环图；

点击查看代码 
#include <iostream>
#include <cstdio>
#include <queue>
using namespace std;
int n, m;
struct sss{
	int t, ne;
	long long w;
}e[500005];
int h[500005], cnt;
void add(int u, int v, long long ww) {
	e[++cnt].t = v;
	e[cnt].ne = h[u];
	h[u] = cnt;
	e[cnt].w = ww;
}
int d[500005];
long long dis[500005];
void topu(int s) {
	for (int i = 1; i <= n; i++) dis[i] = -0x3f3f3f3f3f3f3f3f;
	queue<int> q;
	q.push(s);
	dis[s] = 0;
	d[s] = 0;
	for (int i = 1; i <= n; i++) {
		if (i == s) continue;
		if (d[i] == 0) {
			for (int j = h[i]; j; j = e[j].ne) {
				int u = e[j].t;
				d[u]--;
			}
		}
	}
	while(!q.empty()) {
		int t = q.front();
		q.pop();
		for (int i = h[t]; i; i = e[i].ne) {
			int u = e[i].t;
			dis[u] = max(dis[u], dis[t] + e[i].w);
			d[u]--;
			if (d[u] == 0) q.push(u);
		}
	}
}
int main() {
	freopen("in.in", "r", stdin);
	freopen("out.out", "w", stdout);
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> n >> m;
	int x, y;
	long long w;
	for (int i = 1; i <= m; i++) {
		cin >> x >> y >> w;
		add(x, y, w);
		d[y]++;
	}
	topu(1);
	if (dis[n] == -0x3f3f3f3f3f3f3f3f) cout << -1;
	else cout << dis[n];
	return 0;
}

Bellman_Ford 以及 SPFA

点击查看代码 
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
int n, m;
struct sss{
	int t, ne, w;
}e[100005];
int h[100005], cnt;
void add(int u, int v, int ww) {
	e[++cnt].t = v;
	e[cnt].w = ww;
	e[cnt].ne = h[u];
	h[u] = cnt;
}
int dis[100005];
bool vis[100005];
void SPFA(int x) {
	memset(dis, 0x3f, sizeof(dis));
	memset(vis, 0, sizeof(vis));
	dis[x] = 0;
	vis[x] = true;
	queue<int> q;
	q.push(x);
	while(!q.empty()) {
		int t = q.front();
		q.pop();
		vis[t] = false; //出队就false；
		for (int i = h[t]; i; i = e[i].ne) {
			int u = e[i].t;
			if (dis[u] > dis[t] + e[i].w) {
				dis[u] = dis[t] + e[i].w;
				if (!vis[u]) {
					q.push(u);
					vis[u] = true;
				}
			}
		}
	}
}
int backup[1005];
int Bellman_Ford(int x, int k, int m) { //k为到点n的最多经过的边数，m为总边数。正确性待检验； 
	memset(dis, 0x3f, sizeof(dis));
	dis[x] = 0;
	for (int i = 0; i < k; i++) {
		memcpy(backup, dis, sizeof(dis)); //备份，防止串联。 
		for (int j = 1; j <= m; j++) {
			int a = e[j].f, b = e[j].t, ww = e[j].w;
			dis[b] = min(dis[b], backup[a] + e[j].w);
		}
	}
	if (dis[n] < 0x3f3f3f3f / 2) {
		return dis[n];
	} else return -1;
}
int main() {
	cin >> n >> m;
	int x, y, w;
	for (int i = 1; i <= m; i++) {
		cin >> x >> y >> w;
		add(x, y, w);
		add(y, x, w);
	}
	Bellman_Ford(1);
	return 0;
}

SPFA判负环

因为SFPA的本质是Bellman-Ford的队列优化，其记录的是从源点到此点最多经过k条边的最短路，所以如果经过n-1次后还能更新，说明图中存在负环；

点击查看代码 
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
int f;
struct sss{
	int t, w, ne;
}e[100005];
int h[100005], cnt;
void add(int u, int v, int ww) {
	e[++cnt].ne = h[u];
	h[u] = cnt;
	e[cnt].t = v;
	e[cnt].w = ww;
}
int dis[100005];
bool vis[100005];
int n, m, w;
int cn[100005]; //c[i]代表第i个点到源点所需边数；
bool SPFA(int x, int n) {
	memset(dis, 0x3f, sizeof(dis));
	memset(vis, 0, sizeof(vis));
	memset(cn, 0, sizeof(cn)); 
	queue<int> q;
	for (int i = 1; i <= n; i++) {
		q.push(i);
		vis[i] = true;
	}
	while(!q.empty()) {
		int t = q.front();
		q.pop();
		vis[t] = false;
		for (int i = h[t]; i != 0; i = e[i].ne) {
			int to = e[i].t;
			if (dis[to] > dis[t] + e[i].w) {
				dis[to] = dis[t] + e[i].w;
				cn[to] = cn[t] + 1;
				if (cn[to] >= n) return true; //满足条件，直接return；
				if (!vis[to]) {
					q.push(to);
					vis[to] = true;
				}
			}
		}
	}
	return false;
}
int main() {
	cin >> f;
	for (int i = 1; i <= f; i++) {
		cin >> n >> m >> w;
		memset(h, 0, sizeof(h));
		for (int j = 1; j <= n; j++) {
			e[j].ne = 0;
			e[j].t = 0;
			e[j].w = 0;
		}
		cnt = 0;
		int u, v, ww;
		for (int j = 1; j <= m; j++) {
			cin >> u >> v >> ww;
			add(u, v, ww);
			add(v, u, ww);
		}
		for (int j = 1; j <= w; j++) {
			cin >> u >> v >> ww;
			add(u, v, -ww);
		}
		if (SPFA(1, n)) {
			cout << "YES" << endl; //有负环； 
		} else {
			cout << "NO" << endl; //无负环； 
		}
	}
	return 0;
}

<3> Tarjan

求强连通分量个数

点击查看代码 
#include <iostream>
#include <cstdio>
#include <stack>
using namespace std;
struct sss{
	int t, ne;
}e[1000005];
int h[1000005], cnt;
void add(int u, int v) {
	e[++cnt].ne = h[u];
	e[cnt].t = v;
	h[u] = cnt;
}
int dfn[1000005], low[1000005];
int num, su;
bool vis[1000005];
int belog[1000005];
stack<int> s;
int d[1000005];
int sum[1000005];
void tarjan(int x) {
	dfn[x] = low[x] = ++num;
	vis[x] = true;
	s.push(x);
	for (int i = h[x]; i; i = e[i].ne) {
		int u = e[i].t;
		if (!dfn[u]) {
			tarjan(u);
			low[x] = min(low[x], low[u]);
		} else if (vis[u]) {
			low[x] = min(low[x], dfn[u]);
		}
	}
	if (dfn[x] == low[x]) {
		su++;
		int t = 0;
		do {
			t = s.top();
			s.pop();
			sum[su]++;
			belog[t] = su;
			vis[t] = false;
		} while(t != x);
	}
}
int n, m;
int main() {
	scanf("%d %d", &n, &m);
	int x, y;
	for (int i = 1; i <= m; i++) {
		scanf("%d %d", &x, &y);
		add(x, y);
	}
	for (int i = 1; i <= n; i++) {
		if (!dfn[i]) tarjan(i);
	}
	printf("%d", su);
	return 0;
}

Tarjan缩点

例题：ATM， 受欢迎的牛；

以前者为例；

点击查看代码 
#include <iostream>
#include <cstdio>
#include <stack>
#include <cstring>
#include <vector>
#include <queue>
using namespace std;
int n, m, st, p;
struct sss{
	int t, ne;
}e[1000005], edge[1000005];
int h[1000005], cnt;
void add(int u, int v) {
	e[++cnt].ne = h[u];
	h[u] = cnt;
	e[cnt].t = v;
}
int he[1000005], ccnt;
void add_2(int u, int v) {
	edge[++ccnt].ne = he[u];
	he[u] = ccnt;
	edge[ccnt].t = v;
}
vector<int> vec;
bool v[1000005], vis[1000005];
int dfn[1000005], low[1000005];
int a[1000005];
int num, su;
int sum[1000005];
stack<int> s;
int start;
int belog[1000005];
void tarjan(int x) {
	dfn[x] = low[x] = ++num;
	vis[x] = true;
	s.push(x);
	for (int i = h[x]; i; i = e[i].ne) {
		int u = e[i].t;
		if (!dfn[u]) {
			tarjan(u);
			low[x] = min(low[x], low[u]);
		} else if (vis[u]) {
			low[x] = min(low[x], dfn[u]);
		}
	}
	if (dfn[x] == low[x]) {
		su++;
		int t = 0;
		do {
			t = s.top();
			s.pop();
			belog[t] = su;
			sum[su] += a[t];
			vis[t] = false;
			if (v[t]) vec.push_back(su);
			if (t == st) start = su;
		} while(t != x);
	}
}
int dis[1000005], vvis[1000005];
void SPFA(int x) {
	memset(vvis, 0, sizeof(vvis));
	queue<int> q;
	vvis[x] = true;
	q.push(x);
	while(!q.empty()) {
		int t = q.front();
		q.pop();
		vvis[x] = false;
		for (int i = he[t]; i; i = edge[i].ne) {
			int u = edge[i].t;
			if (dis[u] < dis[t] + sum[u]) { //不要吧u写成i！
				dis[u] = dis[t] + sum[u];
				if (!vvis[u]) {
					q.push(u);
					vvis[u] = true;
				}
			}
		}
	}
}
int main() {
	scanf("%d %d", &n, &m);
	int x, y;
	for (int i = 1; i <= m; i++) {
		scanf("%d %d", &x, &y);
		add(x, y);
	}
	for (int i = 1; i <= n; i++) {
		scanf("%d", &a[i]);
	}
	scanf("%d %d", &st, &p);
	for (int i = 1; i <= p; i++) {
		scanf("%d", &x);
		v[x] = true;
	}
	for (int i = 1; i <= n; i++) {
		if (!dfn[i]) tarjan(i);
	}
	for (int i = 1; i <= n; i++) {
		for (int j = h[i]; j; j = e[j].ne) {
			int u = e[j].t;
			if (belog[i] != belog[u]) {
				add_2(belog[i], belog[u]);
			}
		}
	}
	for (int i = 1; i <= su; i++) dis[i] = sum[i];
	SPFA(start);
	int ma = -1;
	for (int i = 0; i < vec.size(); i++) {
		ma = max(ma, dis[vec[i]]);
	}
	printf("%d", ma);
	return 0;
}

求割点

例题：备用交换机

点击查看代码 
#include <iostream>
#include <cstdio>
#include <cstring>
#include <stack>
using namespace std;
int n;
struct sss{
	int t, ne;
}e[10000005];
int h[10000005], cnt;
void add(int u, int v) {
	e[++cnt].ne = h[u];
	h[u] = cnt;
	e[cnt].t = v;
}
stack<int> s;
int dfn[1000005], low[1000005];
int d[1000005];
bool vis[1000005], cd[1000005];
int num;
int sum;
int root;
void tarjan(int x) {
	dfn[x] = low[x] = ++num;
	int son = 0;
	s.push(x);
	vis[x] = true;
	for (int i = h[x]; i; i = e[i].ne) {
		int u = e[i].t;
		if (!dfn[u]) {
			son++;
			tarjan(u);
			low[x] = min(low[x], low[u]);
			if (low[u] >= dfn[x]) {
				if (x != root || son > 1) cd[x] = true;
			}
		} else  {
			low[x] = min(low[x], dfn[u]);
		}
	}
	
}
int main() {
	scanf("%d", &n);
	int x, y;
	while(scanf("%d %d", &x, &y) != EOF) {
		add(x, y);
		add(y, x);
	}
	for (int i = 1; i <= n; i++) {
		if (!dfn[i]) {
			root = i;
			tarjan(i);
		}
	}
	for (int i = 1; i <= n; i++) {
		if (cd[i]) sum++;
	}
	printf("%d\n", sum);
	for (int i = 1; i <= n; i++) {
		if (cd[i]) printf("%d\n", i);
	}
	return 0;
}

求割点与乘法原理的结合

例题：BLO；

点击查看代码 
#include <iostream>
#include <cstdio>
#include <stack>
using namespace std;
int n, m;
struct sss{
	int t, ne;
}e[1000005];
int h[1000005], cnt;
void add(int u, int v) {
	e[++cnt].ne = h[u];
	h[u] = cnt;
	e[cnt].t = v;
}
int dfn[1000005], low[1000005];
int num;
stack<int> s;
bool vis[1000005];
long long ans[1000005];
long long sum[1000005];
bool cd[1000005];
void tarjan(int x) {
	dfn[x] = low[x] = ++num;
	vis[x] = true;
	s.push(x);
	int son = 0;
	sum[x] = 1;
	int su = 0;
	for (int i = h[x]; i; i = e[i].ne) {
		int u = e[i].t;
		if (!dfn[u]) {
			son++;
			tarjan(u);
			sum[x] += sum[u];
			low[x] = min(low[x], low[u]);
			if (low[u] >= dfn[x]) {
				su += sum[u];
				ans[x] += sum[u] * (n - sum[u]);
				if (x != 1 || son > 1) {
					cd[x] = true;
				}
			}
		} else if (vis[u]) {
			low[x] = min(low[x], dfn[u]);
		}
	}
	if (cd[x]) {
		ans[x] += (long long)(n - su - 1) * (su + 1) + n - 1;
	} else {
		ans[x] = (n - 1) << 1;
	}
	if (dfn[x] == low[x]) {
		int t = 0;
		do {
			t = s.top();
			s.pop();
			vis[t] = false;
		} while(t != x);
	}
}
int main() {
	scanf("%d %d", &n, &m);
	int x, y;
	for (int i = 1; i <= m; i++) {
		scanf("%d %d", &x, &y);
		add(x, y);
		add(y, x);
	}
	tarjan(1);
	for (int i = 1; i <= n; i++) {
		printf("%lld\n", ans[i]);
	}
	return 0;
}

求割边

例题：旅游航道；

点击查看代码 
#include <iostream>
#include <cstdio>
#include <cstring>
#include <stack>
using namespace std;
int n, m;
struct sss{
	int t, ne;
}e[1000005];
int h[1000005], cnt;
void add(int u, int v) {
	e[++cnt].ne = h[u];
	h[u] = cnt;
	e[cnt].t = v;
}
int dfn[1000005], low[1000005];
int num;
stack<int> s;
int ans;
bool vis[1000005];
bool bri[1000005];
void tarjan(int x, int fa) {
	dfn[x] = low[x] = ++num;
	vis[x] = true;
	s.push(x);
	bool first = true;
	for (int i = h[x]; i; i = e[i].ne) {
		int u = e[i].t;
		if (u == fa && first) {
			first = false;
			continue;
		}
		if (!dfn[u]) {
			tarjan(u, x);
			low[x] = min(low[x], low[u]);
			if (low[u] > dfn[x]) {
				ans++;
				bri[i] = bri[i ^ 1] = true;
			}
		} else if (vis[u]) {
			low[x] = min(low[x], dfn[u]);
		}
	}
	if (dfn[x] == low[x]) {
		int t = 0;
		do {
			t = s.top();
			s.pop();
			vis[t] = false;
		} while(t != x);
	}
}
int main() {
	scanf("%d %d", &n, &m);
	while(n != 0 && m != 0) {
		int x, y;
		memset(e, 0, sizeof(e));
		memset(h, 0, sizeof(h));
		memset(dfn, 0, sizeof(dfn));
		memset(low, 0, sizeof(low));
		memset(vis, 0, sizeof(vis));
		memset(bri, 0, sizeof(bri));
		num = 0;
		cnt = 0;
		ans = 0;
		while(!s.empty()) s.pop();
		for (int i = 1; i <= m; i++) {
			scanf("%d %d", &x, &y);
			add(x, y);
			add(y, x);
		}
		for (int i = 1; i <= n; i++) {
			if (!dfn[i]) tarjan(i, 0);
		}
		printf("%d\n", ans);
		scanf("%d %d", &n, &m);
	}
	return 0;
}

求边双并重新建没有桥的图

例题：Redundant Paths 分离的路径；

点击查看代码 
#include <iostream>
#include <cstdio>
#include <stack>
#include <vector>
using namespace std;
int n, m;
struct sss{
	int t, ne;
}e[1000005];
int h[1000005], cnt;
void add(int u, int v) {
	e[++cnt].ne = h[u];
	h[u] = cnt;
	e[cnt].t = v;
}
int dfn[1000005], low[1000005];
int num;
int d[1000005];
stack<int> s;
int su;
int belog[1000005];
vector<int> ed[1000005];
void tarjan(int x, int id) {
	dfn[x] = low[x] = ++num;
	s.push(x);
	for (int i = h[x]; i; i = e[i].ne) {
		int u = e[i].t;
		if (i == (id ^ 1)) continue;
		if (!dfn[u]) {
			tarjan(u, i);
			low[x] = min(low[x], low[u]);
		} else {
			low[x] = min(low[x], dfn[u]);
		}
	}
	if (dfn[x] == low[x]) {
		int t = 0;
		su++;
		do {
			t = s.top();
			s.pop();
			belog[t] = su;
			ed[t].push_back(t);
		} while(t != x);
	}
}
int main() {
	scanf("%d %d", &n, &m);
	int x, y;
	cnt = 1;
	for (int i = 1; i <= m; i++) {
		scanf("%d %d", &x, &y);
		add(x, y);
		add(y, x);
	}
	tarjan(1, 1);
	for (int i = 1; i <= n; i++) {
		for (int j = h[i]; j; j = e[j].ne) {
			int u = e[j].t;
			if (belog[i] != belog[u]) {
//				d[belog[i]]++;
				d[belog[u]]++; //无向边i和u强连通，所以只需加一次，且加哪个都行；
			}
		}
	}
	long long ans = 0;
	for (int i = 1; i <= su; i++) {
		if (d[i] == 1) ans++;
	}
	printf("%lld", (ans + 1) >> 1);
	return 0;
}

求边双

P8436 【模板】边双连通分量 ](https://www.luogu.com.cn/problem/P8436 "Luogu P8436 【模板】边双连通分量 ")

点击查看代码 
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;
int n, m;
struct sss{
	int t, ne;
}e[5000005];
int h[5000005], cnt;
void add(int u, int v) {
	e[++cnt].t = v;
	e[cnt].ne = h[u];
	h[u] = cnt;
}
int tot;
bool vis[500005];
vector<int> v[500005];
int dfn[500005], low[500005], dcnt;
bool bri[5000005];
void Tarjan(int x, int id) {
	dfn[x] = low[x] = ++dcnt;
	for (int i = h[x]; i; i = e[i].ne) {
		if (i == (id ^ 1)) continue;
		int u = e[i].t;
		if (!dfn[u]) {
			Tarjan(u, i);
			low[x] = min(low[x], low[u]);
			if (low[u] > dfn[x]) {
				bri[i] = bri[i ^ 1] = true;
			}
		} else {
			low[x] = min(low[x], dfn[u]);
		}
	}
}
void dfs(int x, int now) {
	vis[x] = true;
	v[now].push_back(x);
	for (int i = h[x]; i; i = e[i].ne) {
		int u = e[i].t;
		if (vis[u] || bri[i]) continue;
		dfs(u, now);
	}
}
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> n >> m;
	int x, y;
	cnt = 1;
	for (int i = 1; i <= m; i++) {
		cin >> x >> y;
		add(x, y);
		add(y, x);
	}
	for (int i = 1; i <= n; i++) {
		if (!dfn[i]) Tarjan(i, 1);
	}
	memset(vis, false, sizeof(vis));
	for (int i = 1; i <= n; i++) {
		if (!vis[i]) dfs(i, ++tot);
	}
	cout << tot << '\n';
	for (int i = 1; i <= tot; i++) {
		cout << v[i].size() << ' ';
		for (int j = 0; j < v[i].size(); j++) {
			cout << v[i][j] << ' ';
		}
		cout << '\n';
	}
	return 0;
}

求点双

Luogu P8435 【模板】点双连通分量

点击查看代码 
#include <iostream>
#include <cstdio>
#include <stack>
#include <vector>
using namespace std;
int n, m;
struct sss{
	int t, ne;
}e[5000005];
int h[5000005], cnt;
void add(int u, int v) {
	e[++cnt].t = v;
	e[cnt].ne = h[u];
	h[u] = cnt;
}
int dfn[500005], low[500005], dcnt;
bool vis[500005];
stack<int> s;
vector<int> v[500005];
int tot;
bool gd[500005];
void Tarjan(int x, int rt) {
	dfn[x] = low[x] = ++dcnt;
	s.push(x);
	vis[x] = true;
	bool vv = false;
	int son = 0;
	for (int i = h[x]; i; i = e[i].ne) {
		int u = e[i].t;
		if (u == x) continue;
		vv = true;
		if (!dfn[u]) {
			son++;
			Tarjan(u, rt);
			low[x] = min(low[x], low[u]);
			if (dfn[x] <= low[u]) {
				if (x != rt || son > 1) gd[x] = true;
				tot++;
				int t = 0;
				do {
					t = s.top();
					s.pop();
					v[tot].push_back(t);
				}while(t != u);
				v[tot].push_back(x);
			}
		} else if (vis[u]) {
			low[x] = min(low[x], dfn[u]);
		}
	}
	if (!vv) v[++tot].push_back(x);
}
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> n >> m;
	int x, y;
	for (int i = 1; i <= m; i++) {
		cin >> x >> y;
		add(x, y);
		add(y, x);
	}
	for (int i = 1; i <= n; i++) {
		if (!dfn[i]) Tarjan(i, i);
	}
	cout << tot << '\n';
	for (int i = 1; i <= tot; i++) {
		cout << v[i].size() << ' ';
		for (int j = 0; j < v[i].size(); j++) {
			cout << v[i][j] << ' ';
		}
		cout << endl;
	}
	return 0;
}

例题：矿场搭建题解；

数据结构模板

树状数组 2024-02-18 星期日

概念类知识

所谓树状数组，即像树的数组，一般应用于求多次前缀和以及区间前缀和的问题中；

其根据节点编号的二进制数的末尾0的个数划分层次，每个节点的管辖范围为2^k，其中k为此节点的二进制数末尾0的个数，并用lowbit实现跳父亲的操作；

所谓lowbit，就是一个数的二进制的从右往左数第一个1出现的位置和这个1右面所有0构成的数，如6 == 110, 则lowbit(6) == 10 == 2; 6 + lowbit(6) == 8 == 1000，则节点8是节点6的父亲（父亲由其儿子数值加和转移而来，具体见下图）；

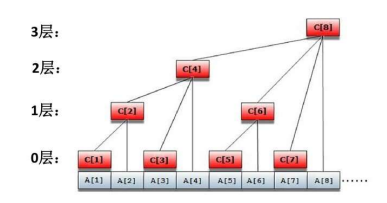
image

一维树状数组

树状数组的主要题目有三类：

1.单点修改，区间查询（树状数组操作的基础，后面的2个操作都是由它转变而来）；

对于单点修改，我们只需先修改它自己，然后一步步修改其父亲即可；

对于区间查询，根据上面的思路，我们可以知道，树状数组可以查询1i的区间和，如果要查询xy的区间和，只需用（1 ~ y） - （1 ~ x - 1）即可；

模板题

点击查看代码 
#include <iostream>
#include <string>
using namespace std;
int n, m;
int a[1000005];
int t[1000005];
string s;
int lowbit(int x) {
	return x & (-x);
}
void add_dian(int x, int k) { //对第x个数加k（单点修改）；
	while(x <= n) {
		t[x] += k;
		x += lowbit(x);
	}
}
int ask_he(int l, int r) { //查询区间和（区间查询）；
	int ans = 0;
	int i = l - 1;
	while(i > 0) {
		ans -= t[i];
		i -= lowbit(i);
	}
	i = r;
	while(i > 0) {
		ans += t[i];
		i -= lowbit(i);
	}
	return ans;
}
int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	for (int i = 1; i <= n; i++) {
		add_dian(i, a[i]);
	}
	cin >> m;
	int c, d;
	for (int i = 1; i <= m; i++) {
		cin >> s;
		cin >> c >> d;
		if (s == "ADD") {
			add_dian(c, d);
		}
		if (s == "SUM") {
			cout << ask_he(c, d) << endl;
		}
	}
	return 0;
}

2.区间修改，单点查询；

对于区间修改，我们如果遍历修改的话会TLE，所以我们要维护原数组的差分数组b，每次修改区间(x, y)时只需修改x 和 y + 1的值即可（将b[x] + k, b[y + 1] - k）；

对于单点查询i，我们只需求b的前缀和(1 ~ i）即可；

记得开long long!

模板题

点击查看代码 
#include <iostream>
#include <string>
using namespace std;
int n, m;
string s;
int a[1000005];
int b[1000005]; //a的差分数组；
int t[1000005]; //维护b的树状数组；
int lowbit(int x) {
	return x & (-x);
}
void add_dian(int x, int k) {
	while(x <= n) {
		t[x] += k;
		x += lowbit(x);
	}
}
//如要进行区间修改，只需将起点加k，终点 + 1减k（差分数组）；
long long ask_dian(int x) { //输出点（a数组中，x为位置）；
	long long ans = 0;
	while(x > 0) {
		ans += t[x];
		x -= lowbit(x);
	}
	return ans;
}
int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	for (int i = 1; i <= n; i++) {
		b[i] = a[i] - a[i - 1];
	}
	for (int i = 1; i <= n; i++) {
		add_dian(i, b[i]);
	}
	cin >> m;
	int c, d, e;
	for (int i = 1; i <= m; i++) {
		cin >> s;
		if (s == "ADD") {
			cin >> c >> d >> e;
			add_dian(c, e);
			add_dian(d + 1, -e);
		}
		if (s == "QUERY") {
			cin >> c;
			cout << ask_dian(c) << endl;
		}
	}
	return 0;
}

3.区间修改，区间查询；
这个比较麻烦，需要推公式，个人感觉最好用线段树做；

公式的推导：

设T(n) 为原数组的前缀和，S(n)为差分数组的前缀和；

则：

\[T(n) == S(1) + S(2) + ... + S(n) \]

\[== b1 + (b1 + b2) + (b1 + b2 + b3) + ... + (b1 + b2 + ... + bn) \]

\[== nb1 + (n - 1)b2 + ... + bn \]

\[== (n + 1)(b1 + b2 + ... + bn) - (b1 + 2b2 + 3b3 + ... + nbn) \]

\[== (n + 1)\sum^{i}_{i <= n} bi - \sum^i_{i <= n} i * bi \]

所以，我们只需维护两个树状数组（差分数组的和i*差分数组的）即可；

模板题

点击查看代码 
#include <iostream>
#include <string>
#include <cstring>
using namespace std;
int n, m;
string s;
int a[100005];
int b[100005]; //a的差分数组；
long long t[100005]; //维护b的树状数组；
long long t1[100005]; //
int lowbit(int x) {
	return x & (-x);
}
void add_dian(int x, long long k) {
	long long val = 1ll * k * x; //(x + a[i]) * y 和 a[i] * y 差 x * y；
	while(x <= n) {
		t[x] += k;
		t1[x] += val;
		x += lowbit(x);
	}
}
void add_dian1(int x, long long k) {
	while(x <= n) {
		t1[x] += k;
		x += lowbit(x);
	}
}
//如要进行区间修改，只需将起点加k，终点减k（差分数组）；
long long ask_sum(int x) {
	long long ans = 0;
	while(x > 0) {
		ans += t[x];
		x -= lowbit(x);
	}
	return ans;
}
long long ask_sum1(int x) {
	long long ans = 0;
	while(x > 0) {
		ans += t1[x];
		x -= lowbit(x);
	}
	return ans;
}
long long ask(int l, int r) {
	long long ans1 = ask_sum(r) * (r + 1) - ask_sum(l - 1) * l; //根据公式(x + 1) * ask_sum(x) - ask_sum1(x)得来（只不过前面的x + 1分开了）（以前是r 和 l - 1，因为公式(x + 1)，所以是(r + 1) 和 l；
	long long ans2 = ask_sum1(r) - ask_sum1(l - 1);
	return ans1 - ans2;
}
int main() {
	memset(t, 0, sizeof(t));
	memset(t1, 0, sizeof(t1));
	memset(a, 0, sizeof(a));
	memset(b, 0, sizeof(b));
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	for (int i = 1; i <= n; i++) {
		b[i] = a[i] - a[i - 1];
	}
	for (int i = 1; i <= n; i++) {
		add_dian(i, b[i]);
	}
	cin >> m;
	int c, d;
	long long e;
	for (int i = 1; i <= m; i++) {
		cin >> s;
		if (s == "ADD") {
			cin >> c >> d >> e;
			add_dian(c, e);
			add_dian(d + 1, -e);
		}
		else {
			cin >> c >> d;
			cout << ask(c, d) << endl;
		}
	}
	return 0;
}

最后，附上例题及题解，辅助理解；

HH的项链
校门外的树

二维树状数组

二维树状数组适用于矩阵，t[x][y]维护从点(1, 1)到点(x, y)的矩阵前缀和；

1.单点修改，区间查询；

前者很简单，只需将一维改为二维即可；

后者的意思是求点(x1, y1)到点(x2, y2)的和；

贴上图，辅助理解；

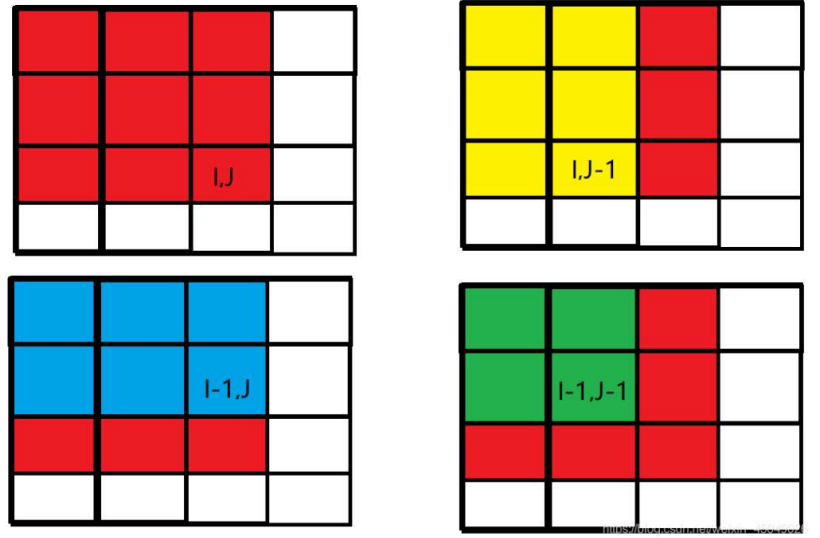
image

先从简单入手，如要求从点(1, 1)到点(x, y)的和，黄色和蓝色部分均已知（前面已经维护过了），则要求的红色部分由黄色 + 蓝色 - 绿色 + a[x][y]即可（a为原数组）；

所以

\[t[i][j] == t[i - 1][j] + t[i][j - 1] - t[i - 1][j - 1] + a[i][j] \]

同理，要求点(x1, y1) 到点(x2, y2)的和，只需将点(1, 1)等效替代为点(x1, y1)即可；

贴图：

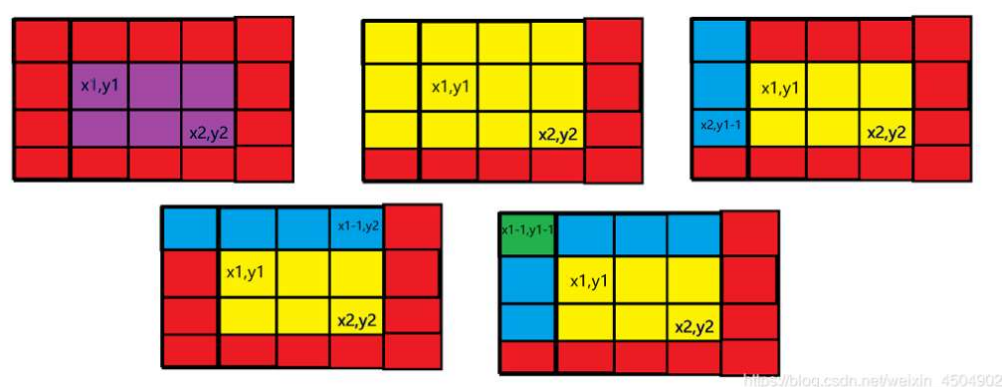
image

如图，已知黄色部分，要求紫色部分，只需用黄色 - 两个蓝色 + 一个绿色即可得出答案；

所以要求的区间和即为

\[t[x2][y2] - t[x2][y1 - 1] - t[x1 - 1][y2] + t[x1 - 1][y1 - 1] \]

模板题

点击查看代码 
#include <iostream>
using namespace std;
int k, a, b, c, d;
int n;
int lowbit(int x) {
	return x & (-x);
}
int t[5005][5005];
void add_dian(int x, int y, int k) { //将点(x, y)增加k；
	for (int i = x; i <= n; i += lowbit(i)) {
		for (int j = y; j <= n; j += lowbit(j)) {
			t[i][j] += k;
		}
	}
}
long long ask_he(int x, int y) { //查询从点(1, 1)到点(x, y)的和；
	long long ans = 0;
	for (int i = x; i > 0; i -= lowbit(i)) {
		for (int j = y; j > 0; j -= lowbit(j)) {
			ans += t[i][j];
		}
	}
	return ans;
}
long long ask(int x1, int y1, int x2, int y2) { //查询从点(x1, y1)到点(x2, y2)的和；
	return ask_he(x2 + 1, y2 + 1) - ask_he(x2 + 1, y1) - ask_he(x1, y2 + 1) + ask_he(x1, y1);
}
int main() {
	cin >> k;
	while(k != 3) {
		if (k == 0) {
			cin >> n;
		} else if (k == 1) {
			cin >> a >> b >> c;
			add_dian(a + 1, b + 1, c);
		} else if (k == 2) {
			cin >> a >> b >> c >> d;
			cout << ask(a, b, c, d) << endl;
		}
		cin >> k;
	}
	return 0;
}

2.区间修改，单点查询；

和一位一样，二维也需要维护一个差分数组；

思考我们维护差分数组的本质---求单点的值；

考虑a数组的前缀和t，由a求t的公式为

\[t[i][j] == t[i - 1][j] + t[i][j - 1] - t[i - 1][j - 1] + a[i][j] \]

设a的差分数组为d，我们知道，a是d的前缀和，则易得

\[a[i][j] == a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + d[i][j] \]

则

\[d[i][j] == a[i][j] - a[i - 1][j] - a[i][j - 1] + a[i - 1][j - 1] \]

这样就可以维护二维差分d了；

对于区间修改，贴上图

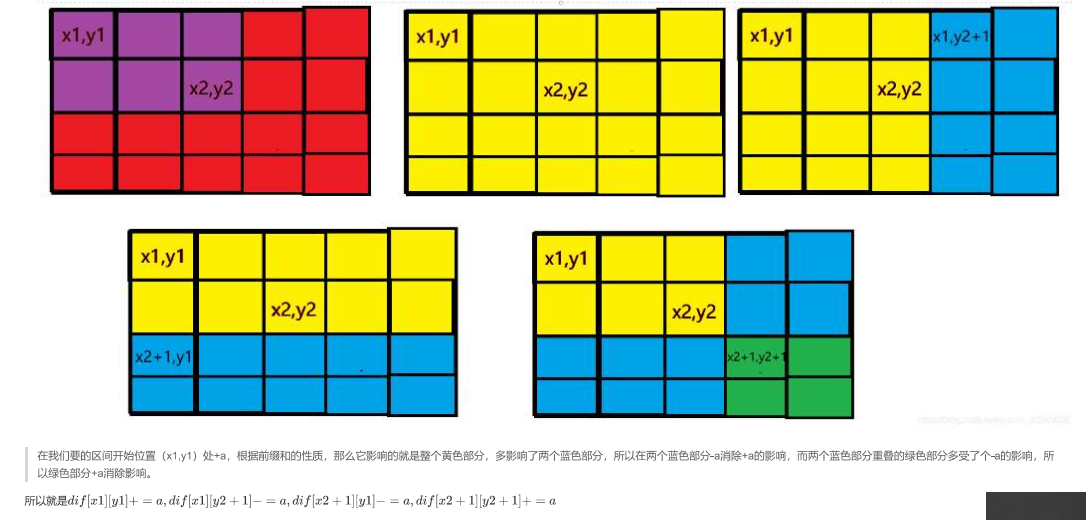
image

模板题

点击查看代码 
#include <iostream>
#include <cstring>
using namespace std;
int t1;
int n, m;
int t[1010][1010];
int lowbit(int x) {
	return x & (-x);
}
void add_dian(int x, int y, int k) { //点(x, y) + k；
	for (int i = x; i <= 1005; i += lowbit(i)) {
		for (int j = y; j <= 1005; j += lowbit(j)) {
			t[i][j] ^= k;
		}
	}
}
long long ask_sum(int x, int y) {
	long long ans = 0;
	for (int i = x; i > 0; i -= lowbit(i)) {
		for (int j = y; j > 0; j -= lowbit(j)) {
			ans ^= t[i][j];
		}
	}
	return ans;
}
int main() {
	cin >> t1;
	while(t1--) {
		cin >> n >> m;
		memset(t, 0, sizeof(t));
		char s;
		int a, b, c, d;
		for (int i = 1; i <= m; i++) {
			cin >> s;
			if (s == 'C') {
				cin >> a >> b >> c >> d;
				add_dian(a, b, 1);
				add_dian(c + 1, d + 1, 1);
				add_dian(c + 1, b, 1);
				add_dian(a, d + 1, 1);
			}
			if (s == 'Q') {
				cin >> a >> b;
				cout << ask_sum(a, b) << endl;
			}
		}
		cout << endl;
	}
	return 0;
}

3.区间修改，区间查询；

太麻烦，不想写了；

直接贴图；

image
image
image

图是从课件上截下来的，课件是image的

文字都是自己写的；

线段树

线段树是一棵二叉搜索树，它支持上述树状数组的全部操作，并支持树状数组外的其它例如求区间最值等的操作，既支持在线操作，也支持离线操作；

线段树与树状数组对比：

优点：线段树适用范围广，当你正确写出板子时，其它操作就变得很简单；

缺点：板子代码量大，容易打错且不易察觉；

常数比树状数组大；

查错麻烦（由于使用递归形式建树及更新值）；

线段树的每个点存储的是一段区间的信息，每个节点的编号是普通二叉树的编号；

所以，对于一个节点x，其左儿子的编号为x << 1；其右儿子的编号为(x << 1) + 1（或者写成更快的位运算x << 1 | 1，因为x << 1为偶数，x << 1 | 1就相当于(x << 1) + 1；

设节点x管辖区间为(l, r)，则定义左儿子管辖区间为(l, mid)，右儿子管辖区间为(mid + 1, r)；

对于一棵二叉树，我们通常使用递归形式建树，先从根节点出发分别递归左右儿子，最后回溯时更新值；

线段树同理，我们使用递归形式建树，先从根节点出发分别递归左右儿子，最后回溯时更新值（一般为区间最值和区间和）；

首先开一个结构体储存该点的区间左右端点，以及区间最值和区间和；

点击查看代码 
struct sss{
	int l, r, ma, sum; //左端点，右端点，区间最大值，区间和；
}tr[50000005]; //要开至少4倍空间，防炸；

建树部分代码：

点击查看代码 
void bt(int id, int l, int r) {
	tr[id].l = l;
	tr[id].r = r;
	if (l == r) {
		tr[id].ma = a[l];
		tr[id].sum = a[l];
		return;
	}
	int mid = (l + r) >> 1;
	bt(ls(id), l, mid);
	bt(rs(id), mid + 1, r);
	tr[id].sum = tr[ls(id)].sum + tr[rs(id)].sum;
	tr[id].ma = max(tr[ls(id)].ma, tr[rs(id)].ma);
}

建完了树，开始操作；

1.单点修改，区间查询；

这个挺简单；

模板题

点击查看代码 
#include <iostream>
#include <string>
using namespace std;
int n, m;
string s;
int a[100005];
struct sss{
	int l, r, ma, sum; //左端点，右端点，区间最大值，区间和；
}tr[50000005]; //要开4倍空间；
int ls(int x) { //x的左孩子编号；
	return x << 1;
}
int rs(int x) { //x的右孩子编号；
	return x << 1 | 1;
}
void bt(int id, int l, int r) {
	tr[id].l = l;
	tr[id].r = r;
	if (l == r) {
		tr[id].ma = a[l];
		tr[id].sum = a[l];
		return;
	}
	int mid = (l + r) >> 1;
	bt(ls(id), l, mid);
	bt(rs(id), mid + 1, r);
	tr[id].sum = tr[ls(id)].sum + tr[rs(id)].sum;
	tr[id].ma = max(tr[ls(id)].ma, tr[rs(id)].ma);
}
void add_dian(int id, int x, int k) { //单点修改，将位置为x的数加上k（id为现在找到的点编号）；
	if (tr[id].l == tr[id].r) {
		tr[id].ma = k;
		tr[id].sum += k; //加k操作； 
		return;
	}
	int mid = (tr[id].l + tr[id].r) >> 1;
	add_dian(x <= mid ? ls(id) : rs(id), x, k); //看看x在左子树还是右子树（注意中点在左子树）；
	tr[id].sum = tr[ls(id)].sum + tr[rs(id)].sum; //更新每个sum值；
	tr[id].ma = max(tr[ls(id)].ma, tr[rs(id)].ma);
}
int ask_sum(int id, int l, int r) { //查询区间(l, r)的和（id为现在找的点的编号）；
	if (tr[id].l >= l && tr[id].r <= r) {
		return tr[id].sum; //如果区间正好被包含就不用找了；
	}
	int mid = (tr[id].l + tr[id].r) >> 1;
	if (r <= mid) return ask_sum(ls(id), l, r);
	else if (l > mid) return ask_sum(rs(id), l, r);
	else return ask_sum(ls(id), l, mid) + ask_sum(rs(id), mid + 1, r);
}
int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	if (n != 0) bt(1, 1, n);
	cin >> m;
	int k, d;
	for (int i = 1; i <= m; i++) {
		cin >> s;
		cin >> k >> d;
		if (s == "ADD") {
			add_dian(1, k, d);
		}
		else if (s == "SUM") {
			cout << ask_sum(1, k, d) << endl;
		}
	}
	return 0;
}

2.区间修改，区间查询及单点查询；

对于区间修改，如果要全部修改的话，从该区间开始要一直修改到根，会TLE；

怎么办呢？

我们引入一个新的东西：懒惰标记；

所谓懒惰标记，即在更新时只更新到管辖此更新区间的子树的根，并将此根的懒惰标记 += 要更新的值，等查询时在下放标记更新它的子节点，这样就可以减少许多不必要的操作，进而避免TLE；

具体更新操作见下面的题；

对于后面的查询，单点查询可以理解成区间长度为1的查询，每次查询从mid递归寻找原区间，最后将答案合并即为最终答案；

模板题

点击查看代码 
#include <iostream> //要开long long, long long, long long!!!!!!!!!!!!!!!!!!!；
#include <string>
using namespace std;
int n, m;
string s;
long long a[10000005];
struct sss{
	int l, r;
	long long ma, sum, lazy; //左端点，右端点，区间最大值，区间和，懒惰标记；long long, long long, long long!!!!!!!!!!!!!!!!!!!!!!!!!；
}tr[50000005]; //要开4倍空间；
int ls(int x) { //x的左孩子编号；
	return x << 1;
}
int rs(int x) { //x的右孩子编号；
	return x << 1 | 1;
}
void bt(int id, int l, int r) {
	tr[id].l = l;
	tr[id].r = r;
	if (l == r) {
		tr[id].ma = a[l];
		tr[id].sum = a[l];
		return;
	}
	int mid = (l + r) >> 1;
	bt(ls(id), l, mid);
	bt(rs(id), mid + 1, r);
	tr[id].sum = tr[ls(id)].sum + tr[rs(id)].sum;
	tr[id].ma = max(tr[ls(id)].ma, tr[rs(id)].ma);
}
void push_down(int id) { //下放标记；
	tr[ls(id)].lazy += tr[id].lazy;
	tr[rs(id)].lazy += tr[id].lazy;
	tr[ls(id)].sum += tr[id].lazy * (tr[ls(id)].r - tr[ls(id)].l + 1);
	tr[rs(id)].sum += tr[id].lazy * (tr[rs(id)].r - tr[rs(id)].l + 1); //sum存储区间总和；
	tr[id].lazy = 0;
}
void add(int id, int a, int b, int l, int r, int k) { //区间修改，将区间(l, r)加k；
	if (l > b || r < a) return;
	if (a >= l && b <= r) {
		tr[id].sum += k * (b - a + 1);
		tr[id].lazy += k;
		return;
	}
	int mid = (a + b) >> 1; //以修改区间为基准，找被修改区间（原区间）；
	push_down(id);
	add(ls(id), a, mid, l, r, k);
	add(rs(id), mid + 1, b, l, r, k);
	tr[id].sum = tr[ls(id)].sum + tr[rs(id)].sum;
}
long long ask_he(int id, int a, int b, int l, int r) { //区间(l, r)查询和；
	if (a > r || b < l) return 0;
	if (a >= l && b <= r) return tr[id].sum;
	int mid = (a + b) >> 1; //同上；
	push_down(id);
	return ask_he(ls(id), a, mid, l, r) + ask_he(rs(id), mid + 1, b, l, r);
}
int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	if (n != 0) bt(1, 1, n);
	cin >> m;
	int k, d, c;
	for (int i = 1; i <= m; i++) {
		cin >> s;
		if (s == "ADD") {
			cin >> k >> d >> c;
			add(1, 1, n, k, d, c);
		} else if (s == "QUERY") {
			cin >> k;
			cout << ask_he(1, 1, n, k, k) << endl;
		}
	}
	return 0;
}

模板题

点击查看代码 
#include <iostream> //要开long long, long long, long long!!!!!!!!!!!!!!!!!!!；
#include <string>
using namespace std;
int n, m;
string s;
long long a[10000005];
struct sss{
	int l, r;
	long long ma, sum, lazy; //左端点，右端点，区间最大值，区间和，懒惰标记；long long, long long, long long!!!!!!!!!!!!!!!!!!!!!!!!!；
}tr[50000005]; //要开4倍空间；
int ls(int x) { //x的左孩子编号；
	return x << 1;
}
int rs(int x) { //x的右孩子编号；
	return x << 1 | 1;
}
void bt(int id, int l, int r) {
	tr[id].l = l;
	tr[id].r = r;
	if (l == r) {
		tr[id].ma = a[l];
		tr[id].sum = a[l];
		return;
	}
	int mid = (l + r) >> 1;
	bt(ls(id), l, mid);
	bt(rs(id), mid + 1, r);
	tr[id].sum = tr[ls(id)].sum + tr[rs(id)].sum;
	tr[id].ma = max(tr[ls(id)].ma, tr[rs(id)].ma);
}
void push_down(int id) { //下放标记；
	tr[ls(id)].lazy += tr[id].lazy;
	tr[rs(id)].lazy += tr[id].lazy;
	tr[ls(id)].sum += tr[id].lazy * (tr[ls(id)].r - tr[ls(id)].l + 1);
	tr[rs(id)].sum += tr[id].lazy * (tr[rs(id)].r - tr[rs(id)].l + 1); //sum存储区间总和；
	tr[id].lazy = 0;
}
void add(int id, int a, int b, int l, int r, int k) { //区间修改，将区间(l, r)加k；
	if (l > b || r < a) return;
	if (a >= l && b <= r) {
		tr[id].sum += k * (b - a + 1);
		tr[id].lazy += k;
		return;
	}
	int mid = (a + b) >> 1; //以修改区间为基准，找被修改区间（原区间）；
	push_down(id);
	add(ls(id), a, mid, l, r, k);
	add(rs(id), mid + 1, b, l, r, k);
	tr[id].sum = tr[ls(id)].sum + tr[rs(id)].sum;
}
long long ask_he(int id, int a, int b, int l, int r) { //区间(l, r)查询和；
	if (a > r || b < l) return 0;
	if (a >= l && b <= r) return tr[id].sum;
	int mid = (a + b) >> 1; //同上；
	push_down(id);
	return ask_he(ls(id), a, mid, l, r) + ask_he(rs(id), mid + 1, b, l, r);
}
int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	if (n != 0) bt(1, 1, n);
	cin >> m;
	int k, d, c;
	for (int i = 1; i <= m; i++) {
		cin >> s;
		cin >> k >> d;
		if (s == "ADD") {
			cin >> c;
			add(1, 1, n, k, d, c);
		} else if (s == "SUM") {
			cout << ask_he(1, 1, n, k, d) << endl;
		}
	}
	return 0;
}

总模板

点击查看代码 
#include <iostream> //要开long long, long long, long long!!!!!!!!!!!!!!!!!!!； 
#include <string>
using namespace std;
int n, m;
string s;
long long a[10000005];
struct sss{
	int l, r;
	long long ma, sum, lazy; //左端点，右端点，区间最大值，区间和，懒惰标记；long long, long long, long long!!!!!!!!!!!!!!!!!!!!!!!!!；
}tr[50000005]; //要开4倍空间；
int ls(int x) { //x的左孩子编号；
	return x << 1;
}
int rs(int x) { //x的右孩子编号；
	return x << 1 | 1;
}
void bt(int id, int l, int r) {
	tr[id].l = l;
	tr[id].r = r;
	if (l == r) {
		tr[id].ma = a[l];
		tr[id].sum = a[l];
		return;
	}
	int mid = (l + r) >> 1;
	bt(ls(id), l, mid);
	bt(rs(id), mid + 1, r);
	tr[id].sum = tr[ls(id)].sum + tr[rs(id)].sum;
	tr[id].ma = max(tr[ls(id)].ma, tr[rs(id)].ma);
}
void add_dian(int id, int x, int k) { //单点修改，将位置为x的数加上k（id为现在找到的点编号）；
	if (tr[id].l == tr[id].r) {
		tr[id].ma = k;
		tr[id].sum += k; //加k操作；
		return;
	}
	int mid = (tr[id].l + tr[id].r) >> 1;
	add_dian(x <= mid ? ls(id) : rs(id), x, k); //看看x在左子树还是右子树（注意中点在左子树）；
	tr[id].sum = tr[ls(id)].sum + tr[rs(id)].sum; //更新每个sum值；
	tr[id].ma = max(tr[ls(id)].ma, tr[rs(id)].ma);
}
long long ask_sum(int id, int l, int r) { //查询区间(l, r)的和（id为现在找的点的编号）；
	if (tr[id].l >= l && tr[id].r <= r) {
		return tr[id].sum; //如果区间被包含就不用找了；
	}
	int mid = (tr[id].l + tr[id].r) >> 1;
	if (r <= mid) return ask_sum(ls(id), l, r);
	else if (l > mid) return ask_sum(rs(id), l, r);
	else return ask_sum(ls(id), l, mid) + ask_sum(rs(id), mid + 1, r);
}
void push_down(int id) { //下放标记；
	tr[ls(id)].lazy += tr[id].lazy;
	tr[rs(id)].lazy += tr[id].lazy;
	tr[ls(id)].sum += tr[id].lazy * (tr[ls(id)].r - tr[ls(id)].l + 1);
	tr[rs(id)].sum += tr[id].lazy * (tr[rs(id)].r - tr[rs(id)].l + 1); //sum存储区间总和；
	tr[id].lazy = 0;
}
void add(int id, int a, int b, int l, int r, int k) { //区间修改，将区间(l, r)加k；
	if (l > b || r < a) return;
	if (a >= l && b <= r) {
		tr[id].sum += k * (b - a + 1);
		tr[id].lazy += k;
		return;
	}
	int mid = (a + b) >> 1; //以修改区间为基准，找被修改区间（原区间）；
	push_down(id);
	add(ls(id), a, mid, l, r, k);
	add(rs(id), mid + 1, b, l, r, k);
	tr[id].sum = tr[ls(id)].sum + tr[rs(id)].sum;
}
long long ask_he(int id, int a, int b, int l, int r) { //区间(l, r)查询和；
	if (a > r || b < l) return 0;
	if (a >= l && b <= r) return tr[id].sum;
	int mid = (a + b) >> 1; //同上；
	push_down(id);
	return ask_he(ls(id), a, mid, l, r) + ask_he(rs(id), mid + 1, b, l, r);
}
int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	if (n != 0) bt(1, 1, n);
	cin >> m;
	int k, d, c;
	for (int i = 1; i <= m; i++) {
		cin >> s;
		if (s == "ADD") {
			cin >> k >> d >> c;
			add(1, 1, n, k, d, c);
		} else if (s == "QUERY") {
			cin >> k;
			cout << ask_he(1, 1, n, k, k) << endl;
		}
	}
	return 0;
}

还有一篇写的不错的博客，可以参考参考（里面的图画的非常详细）；、

线段树合并

Luogu P4556 [Vani有约会] 雨天的尾巴 /【模板】线段树合并

看看板子理解一下，主要是复习用；

合并的过程就是暴力合并管辖相同范围的两棵树的两个节点，若两个节点中有一个没值，则返回另一个。若都有值，则继续向下递归直到叶子节点；

用的是动态开点线段树，时间复杂度约为单次 $ \Theta(\log n) $；

点击查看代码 
#include <iostream>
#include <cstdio>
using namespace std;
int n, m;
int tot;
struct sss{
	int t, ne;
}e[500005];
int h[500005], cnt;
int f[100005][35], dep[5000005], rt[5000005], sum[5000005], kind[5000005], ls[5000005], rs[5000005];
int ans[500005];
void add(int u, int v) {
	e[++cnt].t = v;
	e[cnt].ne = h[u];
	h[u] = cnt;
}
void dfs(int x, int fa) {
	f[x][0] = fa;
	dep[x] = dep[fa] + 1;
	for (int i = h[x]; i; i = e[i].ne) {
		int u = e[i].t;
		if (u == fa) continue;
		dfs(u, x);
	}
}
int lca(int x, int y) {
	if (x == y) return x;
	if (dep[x] < dep[y]) swap(x, y);
	for (int i = 30; i >= 0; i--) {
		if (dep[f[x][i]] >= dep[y]) x = f[x][i];
	}
	if (x == y) return x;
	for (int i = 30; i >= 0; i--) {
		if (f[x][i] != f[y][i]) {
			x = f[x][i];
			y = f[y][i];
		}
	}
	return f[x][0];
}
inline void push_up(int id) {
	if (sum[ls[id]] < sum[rs[id]]) {
		kind[id] = kind[rs[id]];
		sum[id] = sum[rs[id]];
		if (sum[id] == 0) kind[id] = 0;
	} else {
		kind[id] = kind[ls[id]];
		sum[id] = sum[ls[id]];
		if (sum[id] == 0) kind[id] = 0;
	}
}
int add(int id, int l, int r, int col, int k) {
	if (!id) id = ++cnt;
	if (l == r) {
		sum[id] += k;
		kind[id] = col;
		return id;
	}
	int mid = (l + r) >> 1;
	if (col <= mid) {
		ls[id] = add(ls[id], l, mid, col, k);
	} else {
		rs[id] = add(rs[id], mid + 1, r, col, k);
	}
	push_up(id);
	return id;
}
int merge(int x, int y, int l, int r) {
	if (!x || !y) return x + y;
	if (l == r) {
		sum[x] += sum[y];
		return x;
	}
	int mid = (l + r) >> 1;
	ls[x] = merge(ls[x], ls[y], l, mid);
	rs[x] = merge(rs[x], rs[y], mid + 1, r);
	push_up(x);
	return x;
}
void ansfs(int x) {
	for (int i = h[x]; i; i = e[i].ne) {
		int u = e[i].t;
		if (u == f[x][0]) continue;
		ansfs(u);
		rt[x] = merge(rt[x], rt[u], 1, 100000);
	}
	ans[x] = kind[rt[x]];
}
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> n >> m;
	int x, y;
	for (int i = 1; i <= n - 1; i++) {
		cin >> x >> y;
		add(x, y);
		add(y, x);
	}
	dfs(1, 0);
	for (int j = 1; j <= 33; j++) {
		for (int i = 1; i <= n; i++) {
			f[i][j] = f[f[i][j - 1]][j - 1];
		}
	}
	int z;
	for (int i = 1; i <= m; i++) {
		cin >> x >> y >> z;
		rt[x] = add(rt[x], 1, 100000, z, 1);
		rt[y] = add(rt[y], 1, 100000, z, 1);
		int lc = lca(x, y);
		rt[lc] = add(rt[lc], 1, 100000, z, -1);
		rt[f[lc][0]] = add(rt[f[lc][0]], 1, 100000, z, -1);
	}
	ansfs(1);
	for (int i = 1; i <= n; i++) cout << ans[i] << endl;
	return 0;
}

线段树分裂

分裂其实就是合并的逆过程，每次递归时把在需要分裂的区间的节点搞出来即可；

不要忘了最后要 $ push \ up $；

Luogu P5494 【模板】线段树分裂

点击查看代码 
#include <iostream>
#include <cstdio>
using namespace std;
int n, m;
int a[5000005];
int rt[5000005], ls[5000005], rs[5000005];
long long sum[5000005];
int idx, cnt, tot;
int cur[5000005];
inline void push_up(int id) {
	sum[id] = sum[ls[id]] + sum[rs[id]];
}
inline int neww() {
	return cnt ? cur[cnt--] : ++tot; //内存回收；
}
inline void del(int &id) {
	ls[id] = rs[id] = sum[id] = 0;
	cur[++cnt] = id;
	id = 0;
}
void bt(int &id, int l, int r) {
	if (!id) id = neww();
	if (l == r) {
		sum[id] = a[l];
		return;
	}
	int mid = (l + r) >> 1;
	bt(ls[id], l, mid);
	bt(rs[id], mid + 1, r);
	push_up(id);
}
void spilt(int &x, int &y, int l, int r, int L, int R) {
	if (r < L || l > R) return;
	if (!x) return;
	if (l >= L && r <= R) {
		y = x;
		x = 0;
		return;
	}
	if (!y) {
		y = neww();
	}
	int mid = (l + r) >> 1;
	spilt(ls[x], ls[y], l, mid, L, R);
	spilt(rs[x], rs[y], mid + 1, r, L, R);
	push_up(x);
	push_up(y);
}
int merge(int x, int y, int l, int r) {
	if (!x || !y) return x + y;
	if (l == r) {
		sum[x] += sum[y];
		del(y);
		return x;
	}
	int mid = (l + r) >> 1;
	ls[x] = merge(ls[x], ls[y], l, mid);
	rs[x] = merge(rs[x], rs[y], mid + 1, r);
	push_up(x);
	del(y);
	return x;
}
long long ask(int id, int l, int r, int L, int R) {
	if (!id) return 0;
	if (l >= L && r <= R) {
		return sum[id];
	}
	int mid = (l + r) >> 1;
	if (R <= mid) return ask(ls[id], l, mid, L, R);
	else if (L > mid) return ask(rs[id], mid + 1, r, L, R);
	else return ask(ls[id], l, mid, L, mid) + ask(rs[id], mid + 1, r, mid + 1, R);
}
void add(int &id, int l, int r, int pos, int d) {
	if (!id) id = neww();
	if (l == r) {
		sum[id] += d;
		return;
	}
	int mid = (l + r) >> 1;
	if (pos <= mid) add(ls[id], l, mid, pos, d);
	else add(rs[id], mid + 1, r, pos, d);
	push_up(id);
}
int ask_kth(int id, int l, int r, int k) {
	if (l == r) return l;
	int mid = (l + r) >> 1;
	if (sum[ls[id]] >= k) {
		return ask_kth(ls[id], l, mid, k);
	} else {
		return ask_kth(rs[id], mid + 1, r, k - sum[ls[id]]);
	}
}
int main() {
	cin >> n >> m;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	idx = 1;
	bt(rt[1], 1, n);
	int s, p, x, y;
	for (int i = 1; i <= m; i++) {
		cin >> s;
		if (s == 0) {
			cin >> p >> x >> y;
			spilt(rt[p], rt[++idx], 1, n, x, y);
		}
		if (s == 1) {
			cin >> p >> x;
			rt[p] = merge(rt[p], rt[x], 1, n);
		}
		if (s == 2) {
			cin >> p >> x >> y;
			add(rt[p], 1, n, y, x);
		}
		if (s == 3) {
			cin >> p >> x >> y;
			cout << ask(rt[p], 1, n, x, y) << endl;
		}
		if (s == 4) {
			cin >> p >> x;
			if (sum[rt[p]] < x) {
				cout << -1 << endl;
			} else {
				cout << ask_kth(rt[p], 1, n, x) << endl;
			}
		}
	}
	return 0;
}

线段树这东西很难调，一定一定要自己静下心来调；

李超线段树

维护在平面直角坐标系中若干条直线（或线段）与一条平行于 $ y $ 轴的直线的若干个交点的纵坐标的最大值；

显然，李超线段树可以应用于维护斜率优化；

好像也可以与树剖结合解决一些问题；

例题： Luogu P4097 【模板】李超线段树 / [HEOI2013] Segment

点击查看代码 
#include <iostream>
using namespace std;
const double eps = 1e-9;
int n;
int ss;
inline int ls(int x) {
	return x << 1;
}
inline int rs(int x) {
	return x << 1 | 1;
}
struct sss{
	double k, b;
}tr[10000005];
int s[10000005]; //维护以前的线段；
int cnt;
int cmp(double x, double y) {
	if (x - y > eps) return 1;
	else if (y - x > eps) return -1;
	else return 0;
}
double calc(int id, int d) {
	return tr[id].b + tr[id].k * d;
}
void add(int x0, int x1, int y0, int y1) { //新加一条线段；
	cnt++;
	if (x0 == x1) {
		tr[cnt].k = 0;
		tr[cnt].b = max(y0, y1);
	} else {
		tr[cnt].k = 1.0 * (y1 - y0) / (x1 - x0);
		tr[cnt].b = y0 - tr[cnt].k * x0;
	}
}
void add_line(int id, int zl, int zr, int u) { //在所找到的区间内判断最优；
	int &v = s[id];
	int mid = (zl + zr) >> 1;
	int bm = cmp(calc(u, mid), calc(v, mid));
	if (bm == 1 || (!bm && u < v)) swap(u, v);
	int bl = cmp(calc(u, zl), calc(v, zl));
	int br = cmp(calc(u, zr), calc(v, zr));
	if (bl == 1 || (!bl && u < v)) {
		add_line(ls(id), zl, mid, u);
	}
	if (br == 1 || (!br && u < v)) {
		add_line(rs(id), mid + 1, zr, u);
	}
}
void pos(int id, int zl, int zr, int l, int r, int u) { //确定直线所在值域；
	if (l <= zl && zr <= r) {
		add_line(id, zl, zr, u);
		return;
	}
	int mid = (zl + zr) >> 1;
	if (l <= mid) pos(ls(id), zl, mid, l, r, u);
	if (r > mid) pos(rs(id), mid + 1, zr, l, r, u);
}
pair<double, int> pm(pair<double, int> x, pair<double, int> y) {
	if (cmp(x.first, y.first) == -1) {
		return y;
	} else if (cmp(x.first, y.first) == 1) {
		return x;
	} else {
		return x.second < y.second ? x : y;
	}
}
pair<double, int> ask(int id, int zl, int zr, int d) {
	if (zl > d || zr < d) return {0, 0};
	int mid = (zl + zr) >> 1;
	double val = calc(s[id], d);
	if (zl == zr) return {val, s[id]};
	return pm({val, s[id]}, pm(ask(ls(id), zl, mid, d), ask(rs(id), mid + 1, zr, d)));
}
int main() {
	cin >> n;
	int ans = 0;
	int k;
	int x0, y0, x1, y1;
	for (int i = 1; i <= n; i++) {
		cin >> ss;
		if (ss == 0) {
			cin >> k;
			int x = (k + ans - 1 + 39989) % 39989 + 1;
			ans = ask(1, 1, 39989, x).second;
			cout << ans << endl;
		}
		if (ss == 1) {
			cin >> x0 >> y0 >> x1 >> y1;
			x0 = (x0 + ans - 1 + 39989) % 39989 + 1;
			x1 = (x1 + ans - 1 + 39989) % 39989 + 1;
			y0 = (y0 + ans - 1 + 1000000000) % 1000000000 + 1;
			y1 = (y1 + ans - 1 + 1000000000) % 1000000000 + 1;
			if (x0 > x1) swap(x0, x1), swap(y0, y1);
			add(x0, x1, y0, y1);
			pos(1, 1, 39989, x0, x1, cnt); //在值域上建立线段树；
		}
	}
	return 0;
}

下面这个模板比较好，但不是这道题的，求的是一次函数的最大和最小值；

点击查看代码 
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int n, m;
long long a[1000005], b[1000005], suma[1000005], sumb[1000005];
long long ansl[1000005], ansr[1000005];
struct sss{
	long long p, k;
	int id;
	inline bool operator <(const sss &A) const {
		return p < A.p;
	}
}q[1000005];
inline bool cmp(sss x, sss y) {
	return x.p > y.p;
}
inline bool cmpx(sss x, sss y) {
	return x.id < y.id;
}
namespace LCSEG{
	inline int ls(int x) {
		return x << 1;
	}
	inline int rs(int x) {
		return x << 1 | 1;
	}
	struct sss{
		int l, r;
		long long k, b;
	}tr[8000005];
	void bt(int id, int l, int r) {
		tr[id].l = l;
		tr[id].r = r;
		tr[id].k = 1e18;
		tr[id].b = 1e18;
		if (l == r) return;
		int mid = (l + r) >> 1;
		bt(ls(id), l, mid);
		bt(rs(id), mid + 1, r);
	}
	void add(int s, int id, long long k, long long b) {
		if (tr[id].k == 1e18) {
			tr[id].k = k;
			tr[id].b = b;
			if (tr[id].l == tr[id].r) return;
			add(s, ls(id), k, b);
			add(s, rs(id), k, b);
		}
		int mid = (tr[id].l + tr[id].r) >> 1;
		if (s == 0) {
			long long mtr = tr[id].k * mid + tr[id].b;
			long long mli = k * mid + b;
			if (mtr < mli) {
				swap(tr[id].k, k);
				swap(tr[id].b, b);
			}
			long long ltr = tr[id].k * tr[id].l + tr[id].b;
			long long lli = k * tr[id].l + b;
			long long rtr = tr[id].k * tr[id].r + tr[id].b;
			long long rli = k * tr[id].r + b;
			if (ltr < lli) add(s, ls(id), k, b);
			else if (rtr < rli) add(s, rs(id), k, b);
		} else if (s == 1) {
			long long mtr = tr[id].k * mid + tr[id].b;
			long long mli = k * mid + b;
			if (mtr > mli) {
				swap(tr[id].k, k);
				swap(tr[id].b, b);
			}
			long long ltr = tr[id].k * tr[id].l + tr[id].b;
			long long lli = k * tr[id].l + b;
			long long rtr = tr[id].k * tr[id].r + tr[id].b;
			long long rli = k * tr[id].r + b;
			if (ltr > lli) add(s, ls(id), k, b);
			else if (rtr > rli) add(s, rs(id), k, b);
		}
	}
	long long ask(int s, int id, long long x) {
		if (tr[id].l == tr[id].r) return tr[id].k * x + tr[id].b;
		int mid = (tr[id].l + tr[id].r) >> 1;
		long long val = tr[id].k * x + tr[id].b;
		if (s == 0) {
			if (x <= mid) return max(val, ask(s, ls(id), x));
			else return max(val, ask(s, rs(id), x));
		} else {
			if (x <= mid) return min(val, ask(s, ls(id), x));
			else return min(val, ask(s, rs(id), x));
		}
	}
}
using namespace LCSEG;
int main() {
	freopen("seq.in", "r", stdin);
	freopen("seq.out", "w", stdout);
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin >> n >> m;
	for (int i = 1; i <= n; i++) {
		cin >> a[i] >> b[i];
		suma[i] = suma[i - 1] + a[i];
		sumb[i] = sumb[i - 1] + b[i];
	}
	bt(1, -1000000, 1000000);
	for (int i = 1; i <= m; i++) {
		cin >> q[i].p >> q[i].k;
		q[i].id = i;
	}
	sort(q + 1, q + 1 + m);
	int ls = 0;
	for (int i = 1; i <= m; i++) {
		for (int j = ls; j < q[i].p; j++) {
			add(1, 1, -sumb[j], suma[j]);
		}
		ansl[q[i].id] = ask(1, 1, q[i].k) * (-1);
		ls = q[i].p;
	}
	sort(q + 1, q + 1 + m, cmp);
	ls = n - 1;
	bt(1, -1000000, 1000000);
	add(0, 1, -sumb[n], suma[n]);
	for (int i = 1; i <= m; i++) {
		for (int j = ls; j > q[i].p; j--) {
			add(0, 1, -sumb[j], suma[j]);
		}
		ansr[q[i].id] = ask(0, 1, q[i].k);
		ls = q[i].p;
	}
	sort(q + 1, q + 1 + m, cmpx);
	for (int i = 1; i <= m; i++) {
		cout << max(ansl[i] + ansr[i], suma[q[i].p] - q[i].k * sumb[q[i].p] + ansl[i]) << '\n';
	}
	return 0;
}

树链剖分

重链剖分

找重链，跳重链；

Luogu P3384 【模板】重链剖分/树链剖分

点击查看代码 
#include <iostream>
#include <cstdio>
using namespace std;
int n, m, r, p;
int a[1000005];
int fa[1000005], dfn[1000005], nfd[1000005], hson[1000005], htop[1000005], siz[1000005], dep[1000005], dcnt;
struct sss{
	int t, ne;
}e[1000005];
int h[1000005], cnt;
void add(int u, int v) {
	e[++cnt].t = v;
	e[cnt].ne = h[u];
	h[u] = cnt;
}
void dfs1(int x, int fat) {
	fa[x] = fat;
	dep[x] = dep[fat] + 1;
	siz[x] = 1;
	hson[x] = -1;
	for (int i = h[x]; i; i = e[i].ne) {
		int u = e[i].t;
		if (u == fat) continue;
		dfs1(u, x);
		siz[x] += siz[u];
		if (hson[x] == -1 || siz[hson[x]] < siz[u]) hson[x] = u;
	}
}
void dfs2(int x, int t) {
	htop[x] = t;
	dcnt++;
	dfn[x] = dcnt;
	nfd[dcnt] = x;
	if (hson[x] == -1) return;
	dfs2(hson[x], t);
	for (int i = h[x]; i; i = e[i].ne) {
		int u = e[i].t;
		if (u != fa[x] && u != hson[x]) dfs2(u, u);
	}
}
namespace seg{
	inline int ls(int x) {
		return x << 1;
	}
	inline int rs(int x) {
		return x << 1 | 1;
	}
	struct sss{
		int l, r, sum, lz;
	}tr[9000005];
	inline void push_up(int id) {
		tr[id].sum = (tr[ls(id)].sum + tr[rs(id)].sum) % p;
	}
	inline void push_down(int id) {
		if (tr[id].lz) {
			tr[ls(id)].lz = (tr[ls(id)].lz + tr[id].lz) % p;
			tr[rs(id)].lz = (tr[id].lz + tr[rs(id)].lz) % p;
			tr[ls(id)].sum = (tr[ls(id)].sum % p + tr[id].lz * (tr[ls(id)].r - tr[ls(id)].l + 1) % p) % p;
			tr[rs(id)].sum = (tr[rs(id)].sum % p + tr[id].lz * (tr[rs(id)].r - tr[rs(id)].l + 1) % p) % p;
			tr[id].lz = 0;
		}
	}
	void bt(int id, int l, int r) {
		tr[id].l = l;
		tr[id].r = r;
		if (l == r) {
			tr[id].sum = a[nfd[l]] % p;
			return;
		}
		int mid = (l + r) >> 1;
		bt(ls(id), l, mid);
		bt(rs(id), mid + 1, r);
		push_up(id);
	}
	void add(int id, int l, int r, int d) {
		if (tr[id].l >= l && tr[id].r <= r) {
			tr[id].sum = (tr[id].sum % p + d * (tr[id].r - tr[id].l + 1) % p) % p;
			tr[id].lz = (tr[id].lz + d) % p;
			return;
		}
		push_down(id);
		int mid = (tr[id].l + tr[id].r) >> 1;
		if (l <= mid) add(ls(id), l, r, d);
		if (r > mid) add(rs(id), l, r, d);
		push_up(id);
	}
	int ask(int id, int l, int r) {
		if (tr[id].l >= l && tr[id].r <= r) {
			return tr[id].sum % p;
		}
		push_down(id);
		int mid = (tr[id].l + tr[id].r) >> 1;
		if (r <= mid) return ask(ls(id), l, r);
		else if (l > mid) return ask(rs(id), l, r);
		else return (ask(ls(id), l, mid) + ask(rs(id), mid + 1, r)) % p;
	}
}
namespace tp{
	void add(int x, int y, int d) {
		while(htop[x] != htop[y]) {
			if (dep[htop[x]] < dep[htop[y]]) swap(x, y);
			seg::add(1, dfn[htop[x]], dfn[x], d);
			x = fa[htop[x]];
		}
		if (dep[x] > dep[y]) swap(x, y);
		seg::add(1, dfn[x], dfn[y], d);
	}
	int ask(int x, int y) {
		int ans = 0;
		while(htop[x] != htop[y]) {
			if (dep[htop[x]] < dep[htop[y]]) swap(x, y);
			ans = (ans % p + seg::ask(1, dfn[htop[x]], dfn[x]) % p) % p;
			x = fa[htop[x]];
		}
		if (dep[x] > dep[y]) swap(x, y);
		ans = (ans % p + seg::ask(1, dfn[x], dfn[y]) % p) % p;
		return ans;
	}
}
int main() {
	cin >> n >> m >> r >> p;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	int xx, yy;
	for (int i = 1; i <= n - 1; i++) {
		cin >> xx >> yy;
		add(xx, yy);
		add(yy, xx);
	}
	dep[r] = 1;
	dfs1(r, 0);
	dfs2(r, r);
	seg::bt(1, 1, dcnt);
	int s;
	int x, y, z;
	for (int i = 1; i <= m; i++) {
		cin >> s;
		if (s == 1) {
			cin >> x >> y >> z;
			tp::add(x, y, z);
		}
		if (s == 2) {
			cin >> x >> y;
			cout << tp::ask(x, y) % p << endl;
		}
		if (s == 3) {
			cin >> x >> y;
			seg::add(1, dfn[x], dfn[x] + siz[x] - 1, y);
		}
		if (s == 4) {
			cin >> x;
			cout << seg::ask(1, dfn[x], dfn[x] + siz[x] - 1) % p << endl;
		}
	}
	return 0;
}

平衡树

例题：Luogu P3369 【模板】普通平衡树

Splay

点击查看代码 
#include <iostream>
#include <cstdio>
using namespace std;
int rt, tot;
int n;
struct sss{
	int fa, ls, rs, val, cnt, sz;
}tr[10000005];
inline int ls(int x) {
	return tr[x].ls;
}
inline int rs(int x) {
	return tr[x].rs;
}
inline int fa(int x) {
	return tr[x].fa;
}
inline void mt(int id) {
	tr[id].sz = tr[ls(id)].sz + tr[rs(id)].sz + tr[id].cnt;
}
inline bool rson(int id) {
	return id == tr[fa(id)].rs;
}
inline void clear(int id) {
	tr[id].fa = tr[id].ls = tr[id].rs = tr[id].val = tr[id].cnt = tr[id].sz = 0;
}
void rotate(int id) {
	int y = tr[id].fa;
	int z = tr[fa(id)].fa;
	bool r = rson(id);
	if (r) {
		tr[y].rs = tr[id].ls;
	} else {
		tr[y].ls = tr[id].rs;
	}
	if (r) {
		if (tr[id].ls) {
			tr[ls(id)].fa = y;
		}
	} else {
		if (tr[id].rs) {
			tr[rs(id)].fa = y;
		}
	}
	if (r) {
		tr[id].ls = y;
	} else {
		tr[id].rs = y;
	}
	tr[y].fa = id;
	tr[id].fa = z;
	if (z) {
		bool ry = (tr[z].rs == y);
		if (ry) {
			tr[z].rs = id;
		} else {
			tr[z].ls = id;
		}
	}
	mt(y);
	mt(id);
}
void splay(int id, int goal) {
	if (goal == 0) rt = id;
	while(tr[id].fa != goal) {
		int f = tr[id].fa;
		int g = tr[fa(id)].fa;
		if (g != goal) {
			if (rson(f) == rson(id)) {
				rotate(f);
			} else {
				rotate(id);
			}
		}
		rotate(id);
	}
}
void add(int k) {
	if (!rt) {
		tot++;
		tr[tot].val = k;
		tr[tot].cnt++;
		rt = tot;
		mt(rt);
		return;
	}
	int now = rt;
	int f = 0;
	while(1) {
		if (tr[now].val == k) {
			tr[now].cnt++;
			mt(now);
			mt(f);
			splay(now, 0);
			break;
		}
		f = now;
		if (tr[now].val < k) {
			now = tr[now].rs;
		} else {
			now = tr[now].ls;
		}
		if (!now) {
			tot++;
			tr[tot].val = k;
			tr[tot].cnt++;
			tr[tot].fa = f;
			if (tr[f].val < k) {
				tr[f].rs = tot;
			} else {
				tr[f].ls = tot;
			}
			mt(tot);
			mt(f);
			splay(tot, 0);
			break;
		}
	}
}
int rk(int k) {
	int ans = 0;
	int now = rt;
	while(1) {
		if (k < tr[now].val) {
			now = tr[now].ls;
		} else {
			ans += tr[ls(now)].sz;
			if (!now) {
				return ans + 1;
			}
			if (k == tr[now].val) {
				splay(now, 0);
				return ans + 1;
			}
			ans += tr[now].cnt;
			now = tr[now].rs;
		}
	}
}
int ask_kth(int k) {
	int now = rt;
	while(1) {
		if (tr[now].ls && k <= tr[ls(now)].sz) {
			now = tr[now].ls;
		} else {
			k -= (tr[ls(now)].sz + tr[now].cnt);
			if (k <= 0) {
				splay(now, 0);
				return tr[now].val;
			}
			now = tr[now].rs;
		}
	}
}
int ask_pre() {
	int now = tr[rt].ls;
	if (!now) return now;
	while(tr[now].rs) now = tr[now].rs;
	splay(now, 0);
	return now;
}
int ask_nxt() {
	int now = tr[rt].rs;
	if (!now) return now;
	while(tr[now].ls) now = tr[now].ls;
	splay(now, 0);
	return now;
}
void del(int k) {
	rk(k);
	if (tr[rt].cnt > 1) {
		tr[rt].cnt--;
		mt(rt);
		return;
	}
	if (!tr[rt].ls && !tr[rt].rs) {
		clear(rt);
		rt = 0;
		return;
	}
	if (!tr[rt].ls) {
		int now = rt;
		rt = tr[rt].rs;
		tr[rt].fa = 0;
		clear(now);
		return;
	}
	if (!tr[rt].rs) {
		int now = rt;
		rt = tr[rt].ls;
		tr[rt].fa = 0;
		clear(now);
		return;
	}
	int now = rt;
	int x = ask_pre();
	tr[rs(now)].fa = x;
	tr[x].rs = tr[now].rs;
	clear(now);
	mt(rt);
}
int main() {
	#ifndef ONLINE_JUDGE
	freopen("in.in", "r", stdin);
	freopen("out.out", "w", stdout);
	#endif
	rt = 0;
	tot = 0;
	cin >> n;
	int s;
	int x;
	for (int i = 1; i <= n; i++) {
		cin >> s >> x;
		if (s == 1) {
			add(x);
		}
		if (s == 2) {
			del(x);
		}
		if (s == 3) {
			cout << rk(x) << endl;
		}
		if (s == 4) {
			cout << ask_kth(x) << endl;
		}
		if (s == 5) {
			add(x);
			cout << tr[ask_pre()].val << endl;
			del(x);
		}
		if (s == 6) {
			add(x);
			cout << tr[ask_nxt()].val << endl;
			del(x);
		}
	}
	return 0;
}

FHQ Treap

点击查看代码 
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <ctime>
using namespace std;
int n;
int rt, tot;
struct sss{
	int ls, rs, val, dat, sz;
}tr[10000005];
inline int ls(int x) {
	return tr[x].ls;
}
inline int rs(int x) {
	return tr[x].rs;
}
inline void mt(int x) {
	tr[x].sz = tr[ls(x)].sz + tr[rs(x)].sz + 1;
}
int neww(int k) {
	tot++;
	tr[tot].val = k;
	tr[tot].dat = rand();
	tr[tot].sz = 1;
	return tot;
}
void split(int id, int k, int &x, int &y) {
	if (!id) {
		x = 0;
		y = 0;
		return;
	}
	if (tr[id].val <= k) {
		x = id;
		split(tr[id].rs, k, tr[id].rs, y);
	} else {
		y = id;
		split(tr[id].ls, k, x, tr[id].ls);
	}
	mt(id);
}
int merge(int x, int y) {
	if (!x || !y) return x + y;
	if (tr[x].dat < tr[y].dat) {
		tr[x].rs = merge(tr[x].rs, y);
		mt(x);
		return x;
	} else {
		tr[y].ls = merge(x, tr[y].ls);
		mt(y);
		return y;
	}
}
int ask_kth(int now, int k) {
	if (!now) {
		return 0;
	}
	while(1) {
		if (k <= tr[ls(now)].sz) {
			now = tr[now].ls;
		} else {
			if (k == tr[ls(now)].sz + 1) {
				return now;
			} else {
				k -= (tr[ls(now)].sz + 1);
				now = tr[now].rs;
			}
		}
	}
}
int main() {
	#ifndef ONLINE_JUDGE
	freopen("in.in", "r", stdin);
	freopen("out.out", "w", stdout);
	#endif
	srand(time(0));
	cin >> n;
	int s, x;
	for (int i = 1; i <= n; i++) {
		cin >> s >> x;
		if (s == 1) {
			int r1 = 0, r2 = 0;
			split(rt, x, r1, r2);
			rt = merge(merge(r1, neww(x)), r2);
		}
		if (s == 2) {
			int r1 = 0, r2 = 0, r3 = 0;
			split(rt, x, r1, r2);
			split(r1, x - 1, r1, r3);
			r3 = merge(tr[r3].ls, tr[r3].rs);
			rt = merge(merge(r1, r3), r2);
		}
		if (s == 3) {
			int r1 = 0, r2 = 0;
			split(rt, x - 1, r1, r2);
			cout << tr[r1].sz + 1 << endl;
			rt = merge(r1, r2);
		}
		if (s == 4) {
			cout << tr[ask_kth(rt, x)].val << endl;
		}
		if (s == 5) {
			int r1 = 0, r2 = 0;
			split(rt, x - 1, r1, r2);
			cout << tr[ask_kth(r1, tr[r1].sz)].val << endl;
			rt = merge(r1, r2);
		}
		if (s == 6) {
			int r1 = 0, r2 = 0;
			split(rt, x, r1, r2);
			cout << tr[ask_kth(r2, 1)].val << endl;
			rt = merge(r1, r2);
		}
	}
	return 0;
}

ST表

$ \Theta(1) $ 查询 $ RMQ $；

Luogu P3865 【模板】ST 表

点击查看代码 
#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
int n, m;
int a[1000005];
int f[500005][35];
int lg[1000005];
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
	while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
	return x*f;
}
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	n = read();
	m = read();
	for (int i = 1; i <= n; i++) {
		a[i] = read();
	}
	lg[1] = 0;
	for (int i = 2; i <= n; i++) {
		lg[i] = lg[i >> 1] + 1;
	}
	int l;
	int r;
	for (int i = 1; i <= n; i++) {
		f[i][0] = a[i];
	}
	for (int j = 1; j <= lg[n]; j++) {
		for (int i = 1; i <= n - (1 << j) + 1; i++) {
			f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
		}
	}
	for (int i = 1; i <= m; i++) {
		l = read();
		r = read();
		int k = lg[r - l + 1];
		cout << max(f[l][k], f[r - (1 << k) + 1][k]) << '\n';
	}
	return 0;
}

字符串

字符串总结；

扩展欧几里得

求 $ ax + by = gcd(a, b) $ 的一组整数解 $ x, y $；

点击查看代码 
#include <iostream>
#include <cstdio>
using namespace std;
int exgcd(int a, int b, int &x, int &y) {
	if (b == 0) {
		y = 0;
		x = 1;
		return a;
	}
	int res = exgcd(b, a % b, x, y);
	int o = x;
	x = y;
	y = o - a / b * y;
	return res;
}
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);

	return 0;
}

对于通解，可以用如下式子：$ x = x_0 + \frac{b}{gcd(a, b)} \times t, \ \ y = y_0 - \frac{a}{gcd(a, b)} \times t $；

其中 $ t $ 为任意整数；

卡特兰数

有数列 1 1 2 5 14 42 132...，则其大概率满足卡特兰数；

通式：$ H(n) = \frac{C_{2n}^{n}}{n + 1} (n \geq 2) $；

欧拉路，欧拉回路（一笔画）

一个无向图有欧拉路，当其有两个奇点时（度为奇数的点），如果在有向图中，满足其他点的入度等于出度，但有一个点入度比出度小一，有另一个大一；

有欧拉回路，在无向图中当其无奇点时，在有向图中当所有点入度等于出度时；

所谓一笔画问题，即从某一个点走，不重复的经过每条边一次到一个点为止，如果回到原点，则这个路径叫欧拉回路；

找路径的话直接 dfs 即可，复杂度 $ \Theta(m) $，其中 $ m $ 为边数；

矩阵乘法

对于两个矩阵，它们两个可以相乘当前一个矩阵的行数等于后一个矩阵的列数时；

也就是说，一个 $ m \times p $ 和一个 $ n \times m $ 的矩阵可以相乘，最后得到一个 $ n \times p $ 的矩阵；

设前一个矩阵是 $ a $，后一个是 $ b $，设答案矩阵为 $ ans $，则 $ ans_{i, j} = \sum_{k = 1}^{m} a_{i, k} \times b_{k, j} $；

矩阵快速幂

对于一些线性递推算法（比如DP），状态转移方程一般是固定的，但当需要递推的次数很多时是不可接受的，这种情况下可以使用矩阵快速幂加速递推；

比如对于斐波那契数列 $ f_n = f_{n - 1} + f_{n - 2} $，求 $ f_{1e9} \mod p $；

当然可以用通项公式做，但如果要递推这么办呢？

发现要递推的项数很多，于是考虑转化为矩阵；

首先考虑转移到 $ f_n $，需要什么，需要 $ f_{n - 1}, f_{n - 2} $；

所以最终的矩阵中有 $ f_n $，初始矩阵中有 $ f_{n - 1}, f_{n - 2} $；

那么我们想要一个递推矩阵（这里的递推矩阵需要是正方形的，不然快速幂的时候形态会变），使得初始矩阵乘递推矩阵等于最终矩阵，然后对递推矩阵做快速幂即可解决这个问题；

考虑递推矩阵的构造，那么设其为 $ A $，那么我们发现， $ A_{1, 1} \times f_{n - 1} + A_{1, 2} \times f_{n - 2} = f_{n} \rightarrow A_{1, 1} = A_{1, 2} = 1 $；

然后最终矩阵还剩下一项，因为要继续递推，所以这一项是 $ f_{n - 1} $；

最后直接快速幂，复杂度 $ \log 1e9 $；

对于快速幂，其实和普通的无异，只不过是重载了乘法运算符；

那么对于这道题的矩阵转移为：

\[\begin{bmatrix} f_{n} \\ f_{n - 1} \\ \end{bmatrix} = \begin{bmatrix} f_{n - 1} \\ f_{n - 2} \\ \end{bmatrix} \times \begin{bmatrix} 1 \ 1 \\ 1 \ 0 \\ \end{bmatrix} \]

在实际情况中，我们要依据状态转移方程去适宜的选择我们矩阵的大小，一般从最终矩阵和初始矩阵入手，找递推矩阵；

To be continued...

posted @ 2024-02-15 15:05  Peppa_Even_Pig  阅读(40)  评论(1)  编辑  收藏  举报