并查集

 引子

在讲并查集之前，我们先分析一个问题：

A有一群职工，B也有一群职工，而B是A的职工，所以B的职工就成了A的职工，这时我们称A为A公司的老板。假设有很多公司，每个公司中有很多职工，询问指定的两个人所属的公司是否相同。

很容易想到一种朴素的算法：把在同一公司人标为一个颜色

 

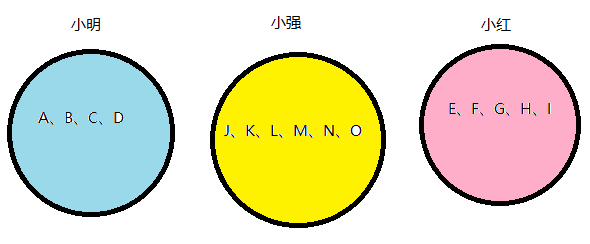
　当小明是小红的职工时，小红的职工就成了小明的职工，所以把他们标为同种颜色，即合并小明和小红的职工们

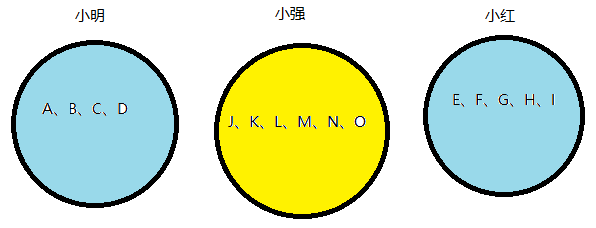
这样我们在判断两个人的是否属于同一公司时只需判断他们的颜色是否相同

so，那么问题来了，如何合并小明和小红的职工们呢？

暴力的搜索出小红的职工们，再把她的职工们变为小明的职工？

一共有n个公司，最坏情况会合并n-1次，时间复杂度为O（n^2），显然是不可接受的。

二、朴素的并查集

还是用这个例子解释

在最初的时候，1、2、3、4、5是五个毫无关系的人，所以他们的老板都只有他们自己

  

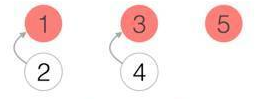
 有一天2加入1的公司，4加入3的公司

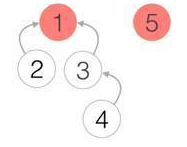
 不久3加入1的公司，所以4也成为了1公司的职工

以上就是并查集的合并操作，那么该如何查找呢？

我们用fa[]数组记录每个人的直接上司（如fa[4]=3,fa[3]=1,fa[2]=1,fa[1]=1）

当我们要找某个人公司的老板，就可以利用他的直接上司（fa数组）向上回溯，直到找到一个老板是自己的人（公司的大boss）

int find(int x)
{
    if(fa[x]==x)  return x;
    return find(fa[x]);
}

但是如果我们这样回溯会浪费时间，在最坏情况下，查找的时间复杂度为O(n)。如果遇到一些比较坑的题会超时，那该怎么办呢？

 

三、路径压缩

这时候，我们就要引入路径压缩这个概念 ，在查找A的老板时，顺便把A的所有上司的fa[]全部变为公司的大老板，这样在下次查找时可以把回溯的深度大大降低（不懂的可以往下看）

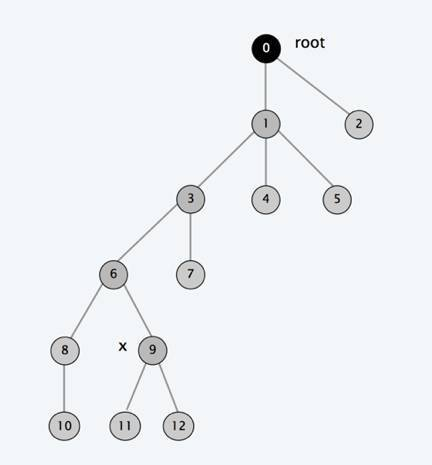
现在我们开始查找9所在公司的老板（fa[9]=6,fa[6]=3,fa[3]=1,fa[1]=0,fa[0]=0）

在我们查找到老板后把途径的所有上司的fa直接指向老板，于是这棵树就变成这样了

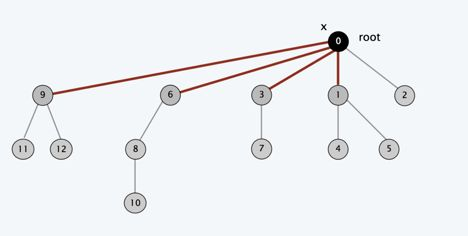
有人可能会问了，这样回溯一遍不是更慢吗。

当我们下次再寻找9所在公司的老板时（fa[9]=0,fa[0]=0）

搜索的深度瞬间缩小了，当这棵树是一条链时，每次查找时间都是O（n）的。但如果用了路径压缩，每次查找的时间复杂度会降低至一个很小的常数

int find(int x)
{
    int p=x,q;
    while(x!=fa[x])//不是根节点
      x=fa[x];
    while(p!=x)//路径压缩，将他们的fa指向根
    {
        q=fa[p];
        fa[p]=x;
        p=q;
    }
    return x;//返回根
}

四、习题（持续更新）

　　1.bzoj4195

　　　　离散化+并查集

　　　　

#include<stdio.h>
#include<algorithm>
#include<string.h>
#include<map>
using namespace std;
int fa[10000000],n,sum[10000000],tot,T;
map<int,int> old,tong;
struct node
{
    int x,y,c;
}a[10000000];
template<class T>void read(T &x)
{
    x=0;char ch=getchar();
    while(ch<'0'||ch>'9')  ch=getchar();
    while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
}
int find(int x)
{
    int p=x,q;
    while(x!=fa[x])
      x=fa[x];
    while(p!=x)
    {
        q=fa[p];
        fa[p]=x;
        p=q;
    }
    return x;
}
int main()
{
    read(T);
    while(T--)
    {
        old.clear();tong.clear();tot=0;bool flag=0;
        read(n);
        for(int i=1;i<=n;i++)
        {
            read(a[i].x);read(a[i].y);read(a[i].c);
            if(tong[a[i].x]==0)
            {   
                tong[a[i].x]=1;
                sum[++tot]=a[i].x;
            }
            if(tong[a[i].y]==0)
            {
                tong[a[i].y]=1;
                sum[++tot]=a[i].y;
            }   
        }
        sort(sum+1,sum+1+tot);
        for(int i=1;i<=tot;i++) old[sum[i]]=i;
        for(int i=1;i<=n;i++)
        {
            a[i].x=old[a[i].x];
            a[i].y=old[a[i].y];
        }       
        for(int i=1;i<=tot;i++) fa[i]=i; 
        for(int i=1;i<=n;i++)
        {
            int p=find(a[i].x),q=find(a[i].y);
            if(a[i].c==1&&p!=q) fa[p]=q;
            if(a[i].c!=1&&p==q){flag=1;break;}
        }
        if(flag==1){printf("NO\n");continue;}
        for(int i=1;i<=n;i++)
        {
            int p=find(a[i].x),q=find(a[i].y);
            if(a[i].c==1&&p!=q){flag=1;break;}
            if(a[i].c==0&&p==q){flag=1;break;}
        }
        if(flag==1)printf("NO\n");
        else printf("YES\n");
    }
    return 0;
}

　　2.poj1456

　　　　贪心+并查集

　　　

#include<stdio.h>
#include<algorithm>
#include<string.h>
using namespace std;
struct node{
    int w,t;
}sell[100007];
int fa[100007],n;
template<class T>void read(T &x)
{
    x=0;char ch=getchar();
    while(ch<'0'||ch>'9')  ch=getchar();
    while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
}
bool cmp(node x,node y)
{
    return x.w>y.w;
}
int find(int x)
{
    int p=x,q;
    while(fa[x]!=-1)
      x=fa[x];
    while(p!=x)
    {
        q=fa[p];
        fa[p]=x;
        p=q;
    }
    return x;
}
int main()
{
    while(scanf("%d",&n)!=EOF)
    {
        int ans=0;
        memset(fa,-1,sizeof(fa));
        for(int i=1;i<=n;++i)
        {
            read(sell[i].w);
            read(sell[i].t);
        }
        sort(sell+1,sell+n+1,cmp);
        for(int i=1;i<=n;++i)
        {
            int q=find(sell[i].t);
            if(q>0)
            {
                  ans+=sell[i].w;
                  fa[q]=q-1;
              }
        }
        printf("%d\n",ans);
    }
    return 0;
}