堆

2.5堆（Heap）的定义和性质

2.5.1堆的定义

优先队列：特殊的“队列”，取出元素的顺序是依照元素的优先权（关键字）大小，而不是元素进入队列的先后顺序。

 

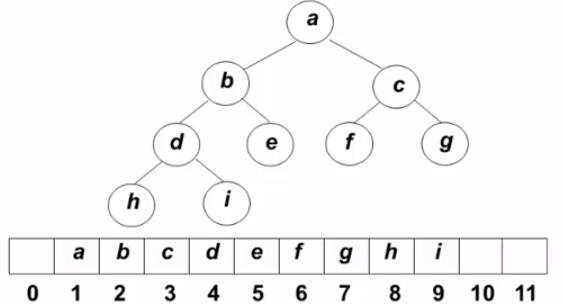
堆的两个特性：

• 结构性：用数组表示的完全二叉树

• 有序性：任一结点的关键字是其子树所有节点的最大值或最小值，最大堆（Max Heap），也称为大顶堆最小堆（Min Heap），也称为小顶堆

 2.5.2最大堆的创建（初始化空堆）

//用数组存储一个堆
typedef struct Heap* MaxHeap;
struct Heap {
    int* Elements;//指向存储堆元素的数组
    int Size;//堆的当前元素个数
    int Capacity;//堆的最大容量
};

MaxHeap Create(int MaxSize) {
    MaxHeap H = (MaxHeap)malloc(sizeof(Heap));
    //从下标为1的位置开始存放
    H->Elements = (int*)malloc((MaxSize + 1) * sizeof(int));
    H->Size = 0;
    H->Capacity = MaxSize;
    H->Elements[0] = MaxData;//"哨兵"，大于堆中所有元素的值
    return H;
}

 

 2.5.3最大堆的插入

将新增结点插入到从其父结点到根结点的有序序列中。

注意，因为有哨兵的存在，所以当i=1的时候循环必然会停止执行

//最大堆的插入 插入元素item
void InsertMaxHeap(MaxHeap H, int item) {
    int i;
    if (H->Size == MaxSize) {
        cout << "最大堆已满";
        return;
    }
    else {
        i = ++H->Size;//i指向插入后堆中最后一个元素的位置
        for (; H->Elements[i / 2] < item; i /= 2) {//如果父结点更小
            H->Elements[i] = H->Elements[i / 2];//将父结点的值赋给当前结点
        }
        H->Elements[i] = item;
    }
}

 

2.5.4最大堆的删除

取出根结点（最大值）元素，同时删除堆的一个结点（最后一个结点），等效于将最后一个结点的元素值替换最大的元素，然后调整成最大堆。

//最大堆的删除
int DeleteMaxHeap(MaxHeap H) {
    int parent, child;
    int MaxItem, tmp;
    if (Isempty(H)) {
        cout << "最大堆已空";
        return 0;
    }
    MaxItem = H->Elements[1];//第一个元素最大
    tmp = H->Elements[H->Size--];//记录最后一个元素
    for (parent = 1; parent * 2 <= H->Size; parent = child) {
        child = parent * 2;//左儿子
        //parent表示tmp当前的位置
        if (child != H->Size&&H->Elements[child] < H->Elements[child + 1])
            child++;
        if (tmp >= H->Elements[child])break;
        else
            H->Elements[parent] = H->Elements[child];
    }
    H->Elements[parent] = tmp;//返回的parent是tmp最终的位置
    return MaxItem;
}

 

2.5.5最大堆的建立

建立最大堆：将已经存在的N个元素按最大堆的要求存放在一个一维数组中

【注】：对于一组相同数据，插入建堆和调整建堆建出来的堆也许不一样

 

【例题】：

 

 

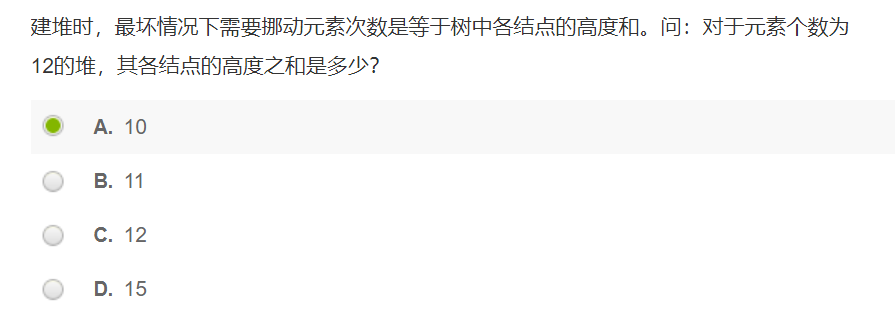
 【分析】：

                1
        2              3  
    4       5       6     7
  8   9  10  11  12

建堆的话，主要考虑下沉的次数，以此定义高度。
这样的话，8,9,10,11,12都是已经沉底的，要注意的是7也是在最底了。这些节点高度都是0。
4,5,6都是最多可以沉1次的，高度为1.
2,3最多能沉2次，高度为2.
1可以沉3次，高度为3.
1*3+2*2+3*1=3+4+3=10

2.5.5.1方法一：插入建堆

//插入建堆
#include "pch.h"
#include <iostream>
#include <cstdlib>
using namespace std;
#define MaxSize 100
#define MaxData 100

//用数组存储一个堆
typedef struct Heap* MaxHeap;
struct Heap {
    int* Elements;//指向存储堆元素的数组
    int Size;//堆的当前元素个数
    int Capacity;//堆的最大容量
};

MaxHeap Create() {
    MaxHeap H = (MaxHeap)malloc(sizeof(Heap));
    //从下标为1的位置开始存放
    H->Elements = (int*)malloc((MaxSize + 1) * sizeof(int));
    H->Size = 0;
    H->Capacity = MaxSize;
    H->Elements[0] = MaxData;//"哨兵"，大于堆中所有元素的值
    return H;
}

//最大堆的插入 插入元素item
void InsertMaxHeap(MaxHeap H, int item) {
    int i;
    if (H->Size == MaxSize) {
        cout << "最大堆已满";
        return;
    }
    else {
        i = ++H->Size;//i指向插入后堆中最后一个元素的位置
        for (; H->Elements[i / 2] < item; i /= 2) {//如果父结点更小
            H->Elements[i] = H->Elements[i / 2];//将父结点的值赋给当前结点
        }
        H->Elements[i] = item;
    }
}

//遍历输出
void HeapTraversal(MaxHeap H) {
    for (int i = 1; i <= H->Size; i++)
        cout << H->Elements[i] << " ";
}

int main() {
    MaxHeap H;
    H = Create();
    int n;
    cin >> n;
    for (int i = 0; i < n; i++) {
        int t;
        cin >> t;
        InsertMaxHeap(H,t);
    }
    HeapTraversal(H);
    return 0;
}

 

2.5.5.2方法二：调整建堆

从最后一个有孩子结点的结点开始，其本身结点和孩子结点共同构成"子最大堆"，借助前面删除的想法，对每个"子最大堆"排序，最后一层层的整合，最后最大堆建成。

#include <iostream>
#include <cstdlib>
using namespace std;
#define MaxSize 100
#define MaxData 100

//用数组存储一个堆
typedef struct Heap* MaxHeap;
struct Heap {
    int* Elements;//指向存储堆元素的数组
    int Size;//堆的当前元素个数
    int Capacity;//堆的最大容量
};

MaxHeap Create() {
    MaxHeap H = (MaxHeap)malloc(sizeof(Heap));
    //从下标为1的位置开始存放
    H->Elements = (int*)malloc((MaxSize + 1) * sizeof(int));
    H->Size = 0;
    H->Capacity = MaxSize;
    H->Elements[0] = MaxData;//"哨兵"，大于堆中所有元素的值
    return H;
}
//将以i为根结点的子堆进行排序
void SortHeap(MaxHeap H,int i) {
    int parent, child;
    int tmp = H->Elements[i];//保存将要进行调整的结点
    for (parent = i;parent*2<=H->Size; parent = child) {
        child = parent * 2;
        if (child != H->Size&&H->Elements[child] < H->Elements[child + 1])
            child++;//找到左右儿子中更大的一个
        if (tmp > H->Elements[child])break;
        else 
            H->Elements[parent] = H->Elements[child];
    }
    H->Elements[parent] = tmp;
}

//调整
void adjust(MaxHeap H) {
    for (int i = H->Size / 2; i > 0; i--)
        SortHeap(H, i);
}


void HeapTraversal(MaxHeap H) {
    for (int i = 1; i <= H->Size; i++)
        cout << H->Elements[i] << " ";
}

int main() {
    MaxHeap H;
    H = Create();
    int n;
    cin >> n;
    for (int i = 0; i < n; i++) {
        cin >> H->Elements[i+1];
        H->Size++;
    }
    adjust(H);
    HeapTraversal(H);
    return 0;
}