平衡二叉树
2.4平衡二叉树
背景:平衡二叉树首先是二叉排序树。基于二叉排序树,发现树越矮查找效率越高,进而发明了二叉平衡树
2.4.1平衡二叉树的定义
平衡因子(BF Balance factor):BF(T)=hL-hR,其中hL和hR分别为T的左、右子树的高度。
平衡二叉树(Balanced Binary Tree)(AVL树):空树或者任一结点左、右子树高度差的绝对值不超过1,即|BF(T)<=1|。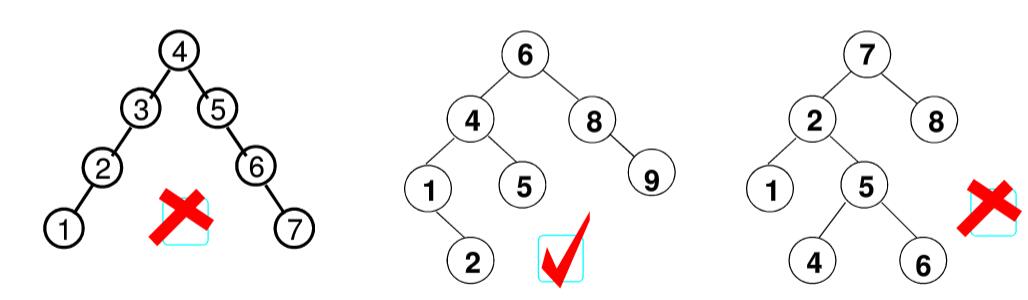
2.4.2平衡二叉树的调整
- 调整之后保证仍然是搜索树
- 从离插入结点最近的结点调整
2.4.2.1RR旋转、
定义:
“麻烦结点(BR的孩子)”在“发现者(A)”右子树的右边,因而叫RR插入,需要RR旋转。
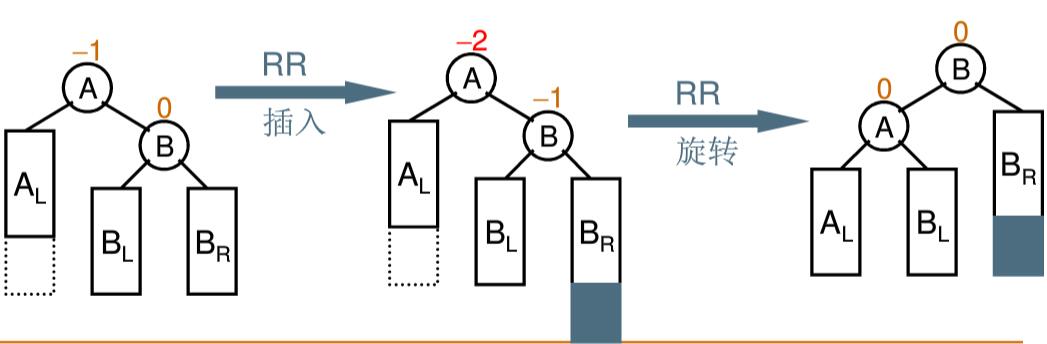
示例:
代码:
1 typedef struct TreeNode* AVLTree; 2 struct TreeNode 3 { 4 int data; 5 AVLTree left; 6 AVLTree right; 7 }; 8 9 AVLTree RR(AVLTree A) { 10 AVLTree B = A->right; 11 A->right = B->left; 12 B->left = A; 13 return B; 14 }
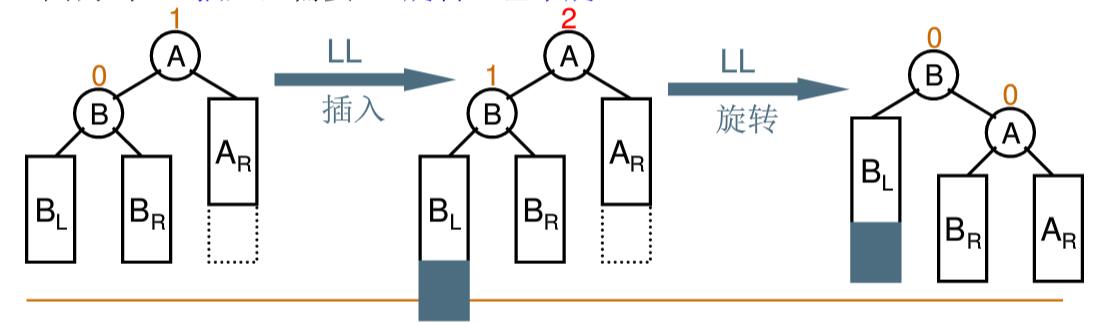
2.4.2.2LL旋转
定义:
“麻烦结点(BL的孩子)”在“发现者(A)”左子树的左边,因而叫LL插入,需要LL旋转。
代码:
1 AVLTree LL(AVLTree A) { 2 AVLTree B = A->left; 3 A->left = B->right; 4 B->right = A; 5 return B;//新的根结点 6 }
2.4.2.3LR旋转
定义:
“麻烦结点(CL或者CR或者两者的孩子)”在"发现结点(A)"的左子树的右边,因而叫LR插入,需要LR旋转。
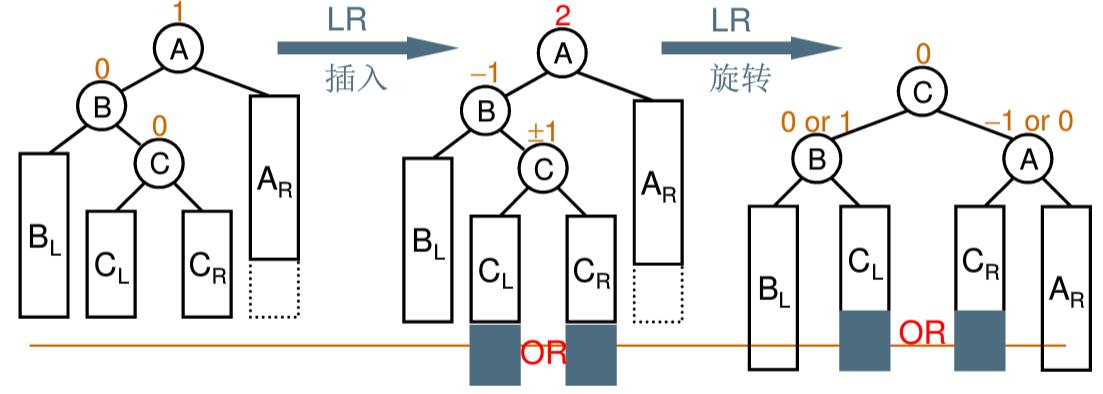
示例:
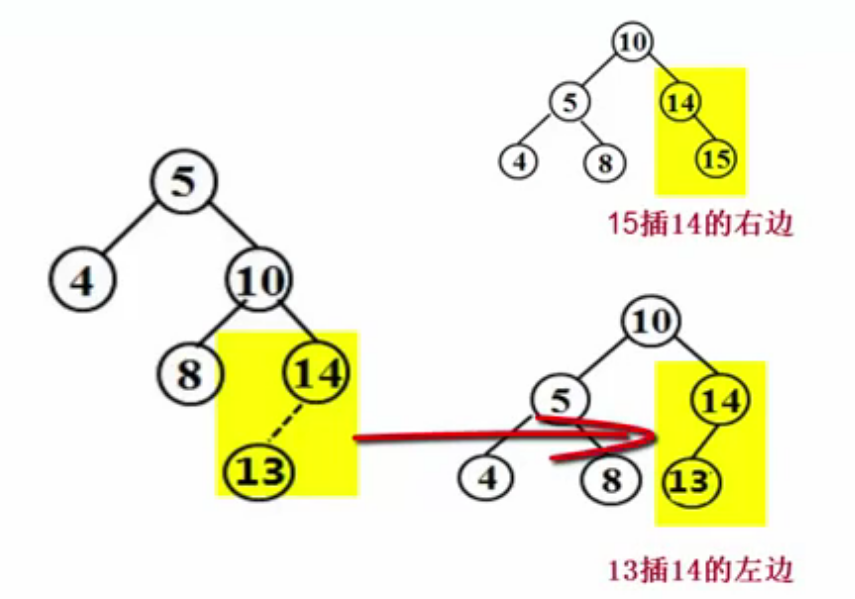
【分析】插入3之后1、4、6的平衡都被破坏了,但是1是距离3最近的结点,故以1为准,3在结点1右子树的右边做RR旋转。

2.4.2.4RL旋转
定义:
“麻烦结点(CL或者CR或者两者的孩子)”在"发现结点(A)"的右子树的左边,因而叫LR插入,需要LR旋转。
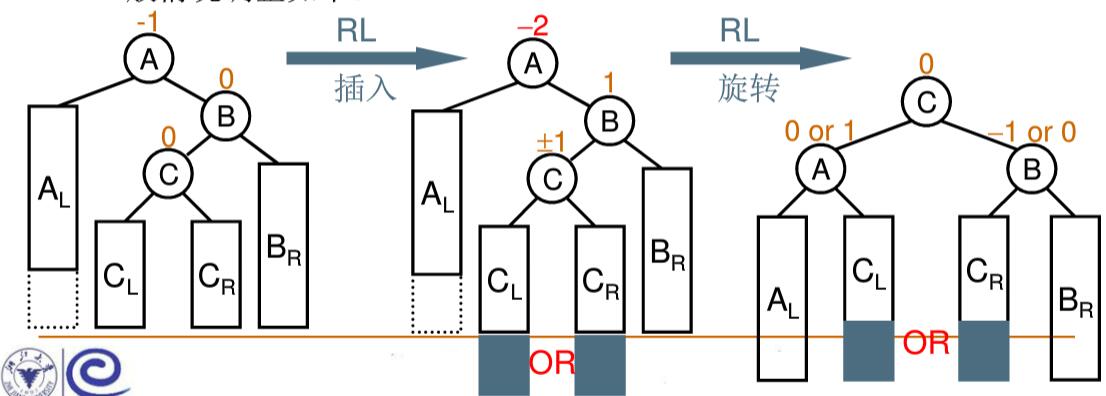
平衡二叉树的实现可见 https://blog.csdn.net/qq_29762941/article/details/81040916
作者:PennyXia
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。


