二叉搜索树

2.4树的应用——二叉搜索树

2.4.1二叉搜索树（Binary Search Tree）的定义与性质

也称为二叉排序树或者二叉搜索树

性质：

  • 非空左子树的所有键值小于其根结点的键值
  • 非空右子树的所有键值大于其根结点的键值
  • 左、右子树都是二叉搜索树

2.4.2二叉搜索树的查找

 1 typedef struct TreeNode* BinTree;
 2 struct TreeNode {
 3     int data;
 4     BinTree left;
 5     BinTree right;
 6 };
 7 
 8 //递归查找 查找元素x
 9 BinTree Find(int x, BinTree BST) {
10     if(BST) {
11         if (x < BST->data)
12             return Find(x, BST->left);
13         else if (x > BST->data)
14             return Find(x, BST->right);
15         else
16             return BST;        
17     }
18     return 0;
19 }
20 //非递归查找，将尾递归函数转化为迭代函数
21 BinTree InterFind(int x, BinTree BST) {
22     if (BST) {
23         if (x < BST->data)
24             BST = BST->left;
25         else if (x > BST->data)
26             BST = BST->right;
27         else
28             return BST;
29     }
30     return 0;
31 }

归纳：查找的效率取决于树的高度

 

查找最大/最小元素：最大元素一定在树的最右边；最小元素一定在树的最左边。

 1 //查找最小元素的递归函数
 2 BinTree FindMin(BinTree BST) {
 3     if (BST) {
 4         if (!BST->left)
 5             return BST;
 6         else
 7             return FindMin(BST->left);
 8     }
 9     return NULL;
10 }
11 //查找最大元素的迭代函数
12 BinTree FinfMax(BinTree BST) {
13     if (BST) {
14         while (BST->right)
15             BST = BST->right;
16         return BST;
17     }
18     return NULL;
19 }

 

2.4.3二叉搜索树的插入

关键是要找到元素应该插入的位置，但是和Find函数不同的是每次要记住插入结点所在子树的根结点，通过递归的方法把下一层的结构返回，然后连接在一起

 1 BinTree Insert(int x, BinTree BST) {
 2     if (!BST) {//如果树为空
 3         BST = (BinTree)malloc(sizeof(TreeNode));
 4         BST->data = x;
 5         BST->left = NULL;
 6         BST->right = NULL;
 7     }
 8     else {
 9         if (x < BST->data)
10             BST->left = Insert(x, BST->left);//在左子树中插入，并且将根结点指向被改变的左子树
11         else
12             BST->right = Insert(x, BST->right);
13     }
14     return BST;//返回的是根结点
15 }

 

2.4.4二叉搜索树的删除

考虑三种情况：

  • 要删除的是叶结点：直接删除，并修改其父结点指针——置为NULL；
  • 要删除的结点只有一个孩子结点：将其父结点的指针指向要删除结点的孩子结点，即其孙子结点；
  • 要删除的结点有左、右两棵树：用另一个结点替代被删除结点，即右子树的最小元素或者左子树的最大元素。其实就是转化成前两种情况，因为最小（最大）元素，一定在最左（最右），一定是叶结点或者只有一个孩子的结点。

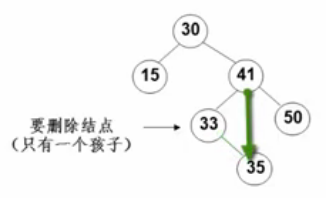
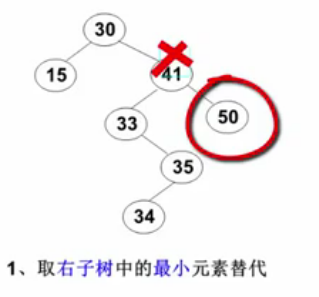
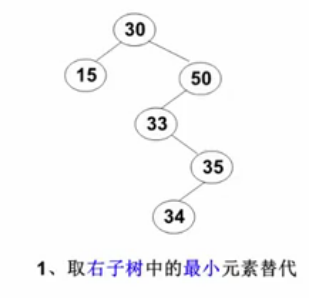
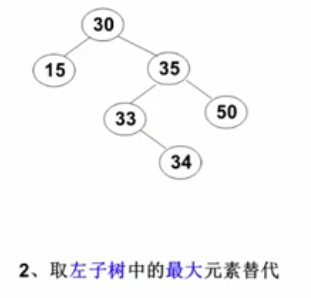
 1 BinTree Delete(int x, BinTree BST) {
 2     BinTree tmp;
 3     //如果是空树
 4     if (!BST)cout << "要删除的元素未找到";
 5     //如果没找到待删除结点
 6     else if (x < BST->data)
 7         //将左子树删除之后的新的根结点挂在左边
 8         BST->left = Delete(x, BST->left);
 9     else if (x > BST->data)
10         BST->right = Delete(x, BST->right);
11     //如果找到待删除结点
12     else {
13         //如果待删除结点有两个孩子
14         if (BST->left&&BST->right) {
15             tmp = FindMin(BST->right);
16             BST->data = tmp->data;//将右子树的最小值的元素覆盖待删除结点
17             BST->right = Delete(tmp->data, BST->right);//删除替代待删除结点的右子树最小值
18         }
19         //如果有一个还是或者没有孩子
20         else {
21             tmp = BST;//直接删除待删除结点
22             //如果没有右孩子，意味着只有左孩子或者没有孩子
23             if (!BST->right)
24                 BST = BST->left;
25             //如果没有左孩子
26             else if (!BST->left)
27                 BST = BST->right;
28             free(tmp);
29         }
30     }
31     return BST;
32 }

 

posted @ 2020-04-03 10:20  PennyXia  阅读(209)  评论(0)  编辑  收藏  举报