树的基本概念
2.1树
2.1.1树(Tree)的定义和性质
n(n>=0)个节点构成的有限集合;当n=0时,称为空树。
对于任何一刻非空树,它具备以下性质:
- 树中有一个称为“根(Root)”的特殊结点,用r表示;
- 其余结点可分为m(m>0)个互不相交的有限集合T1、T2...Tm,其中每个集合本身又是一棵树,称为原来树的“子树”【递归思想】。
- 子树是不相交的
- 除了根结点外,每个结点有且仅有一个父结点
- 一棵N个结点的树有N-1条边
2.1.2树的基本术语
- 结点的度(Degree):结点的子树个数
- 树的度:树的所有结点中最大的度数
- 叶节点(Leaf):度为0的结点
- 父结点(Parent):有子树的结点是其子树的根结点的父结点
- 子结点(Child):若 A 结点是 B 结点的父结点,则称 B 结点是 A 结点的子结点,也称孩子结点
- 兄弟结点(Sibling):具有同一父结点的各个结点彼此是兄弟结点
- 路径和路径长度:从结点n1到nk的路径为一个结点序列n1、n2...nk,路径所包含边的个数为路径长度
- 祖先结点(Ancestor):沿树根到某一结点路径上的所有结点都是这个结点的祖先结点
- 子孙结点(Descendant):某一结点的子树中的所有结点是这个结点的子孙
- 结点的层次(Level):规定根结点在 1 层,其他任一结点的层数是其父结点的层数加一
- 树的深度(Depth):树中所有结点中的最大层次是这棵树的深度
2.1.3树的表示
儿子-兄弟表示法
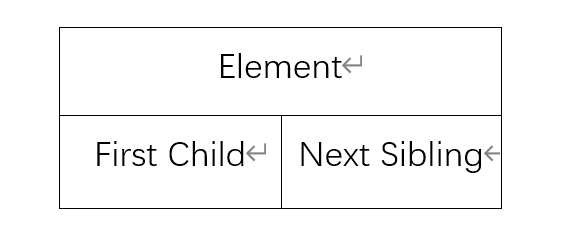
- Element:结点的值
- First Child:指向第一个儿子
- Next Sibling:指向兄弟
二叉树表示法
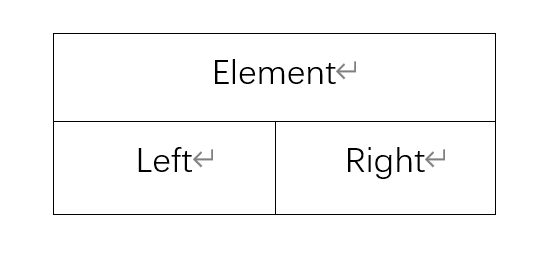
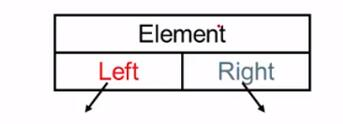
- Element:结点的值
- Left:指向左子树
- Right:指向右子树
2.2二叉树
2.2.1二叉树(Binary Tree)的定义和性质
- 一个有穷的结点集合,可为空;若不为空,则他用根结点和称为其左子树TL和右子树TR的两个不相交二叉树组成。
- 五种具体形态:∅和以下四种
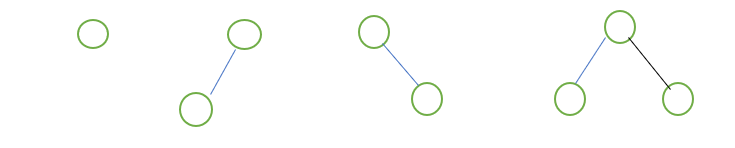
- 二叉树的子树有左右之分
2.2.2特殊二叉树
(1)斜二叉树
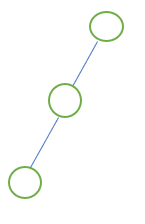
(2)完美/满二叉树:两个子树;叶结点对齐
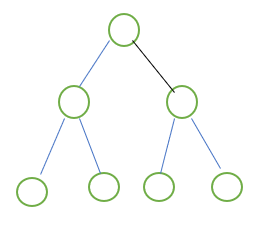
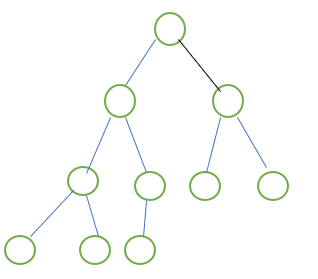
(3)完全二叉树
有 n 个结点的二叉树,对树中结点按从上至下、从左到右顺序进行编号,编号为 i(1 ≤ i ≤ n)结点与满二叉树中编号为 i 结点在二叉树中位置相同
2.2.3二叉树的几个重要性质
- 一个二叉树第i层的最大结点数为2i-1,i>=1
- 深度为k的二叉树有最大结点总数为2k-1,k>=1
- 对于任意非空二叉树T,若n0表示叶结点的个数,n2是度为2的非叶结点的个数,那么n0=n2+1(证明:利用总结点个数和总边数的关系)。
2.2.4二叉树的存储结构
顺序存储结构(将二叉树看成是完全二叉树,没有结点的地方空出来)
- 非根结点(序号 i > 1)的父结点的序号是 ⌊i/2⌋(向下取整)
- 结点(序号为 i)的左孩子结点的序号是 2i(若 2 i ≤ n,否则没有左孩子
- 结点(序号为 i)的右孩子结点的序号是 2i+1(若 2 i +1 ≤ n,否则没有右孩子

链表存储
- Element:结点的值
- Left:指向左子树
- Right:指向右子树
1 typedef struct TreeNode *BinTree; 2 struct TreeNode{ 3 Element Data; // 存值 4 BinTree Left; // 左儿子结点 5 BinTree Right; // 右儿子结点 6 }
作者:PennyXia
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。


