伸展树(splay)

作者：Vamei 出处：http://www.cnblogs.com/vamei 欢迎转载，也请保留这段声明。谢谢！

我们讨论过，树的搜索效率与树的深度有关。二叉搜索树的深度可能为n，这种情况下，每次搜索的复杂度为n的量级。AVL树通过动态平衡树的深度，单次搜索的复杂度为log(n) (以上参考纸上谈兵 AVL树)。我们下面看伸展树(splay tree)，它对于m次连续搜索操作有很好的效率。

伸展树会在一次搜索后，对树进行一些特殊的操作。这些操作的理念与AVL树有些类似，即通过旋转，来改变树节点的分布，并减小树的深度。但伸展树并没有AVL的平衡要求，任意节点的左右子树可以相差任意深度。与二叉搜索树类似，伸展树的单次搜索也可能需要n次操作。但伸展树可以保证，m次的连续搜索操作的复杂度为mlog(n)的量级，而不是mn量级。

具体来说，在查询到目标节点后，伸展树会不断进行下面三种操作中的一个，直到目标节点成为根节点（注意，祖父节点是指父节点的父节点）

1. zig: 当目标节点是根节点的左子节点或右子节点时，进行一次单旋转，将目标节点调整到根节点的位置。

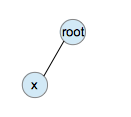
zig

2. zig-zag: 当目标节点、父节点和祖父节点成"zig-zag"构型时，进行一次双旋转，将目标节点调整到祖父节点的位置。

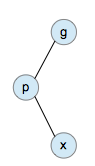
zig-zag

3. zig-zig：当目标节点、父节点和祖父节点成"zig-zig"构型时，进行一次zig-zig操作，将目标节点调整到祖父节点的位置。

zig-zig

单旋转操作和双旋转操作见AVL树。下面是zig-zig操作的示意图:

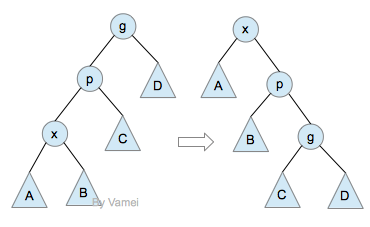
zig-zig operation

在伸展树中，zig-zig操作(基本上)取代了AVL树中的单旋转。通常来说，如果上面的树是失衡的，那么A、B子树很可能深度比较大。相对于单旋转(想一下单旋转的效果)，zig-zig可以将A、B子树放在比较高的位置，从而减小树总的深度。

下面我们用一个具体的例子示范。我们将从树中搜索节点2：

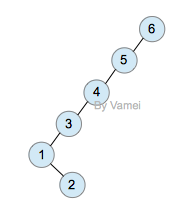
Original

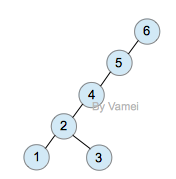
zig-zag (double rotation)

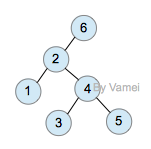
zig-zig

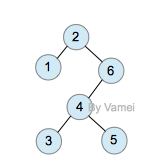
zig (single rotation at root)

上面的第一次查询需要n次操作。然而经过一次查询后，2节点成为了根节点，树的深度大减小。整体上看，树的大部分节点深度都减小。此后对各个节点的查询将更有效率。

伸展树的另一个好处是将最近搜索的节点放在最容易搜索的根节点的位置。在许多应用环境中，比如网络应用中，某些固定内容会被大量重复访问(比如江南style的MV)。伸展树可以让这种重复搜索以很高的效率完成。

伸展树的C实现

  1 /* By Vamei */
  2 /* Splay Tree */
  3 #include <stdio.h>
  4 #include <stdlib.h>
  5 
  6 typedef struct node *position;
  7 typedef int ElementTP;
  8 
  9 struct node {
 10     position parent;
 11     ElementTP element;
 12     position lchild;
 13     position rchild;
 14 };
 15 
 16 /* pointer => root node of the tree */
 17 typedef struct node *TREE;
 18 
 19 TREE find_value(TREE, ElementTP);
 20 position insert_value(TREE, ElementTP);
 21 
 22 static void splay_tree(TREE, position);
 23 static position search_value(TREE, ElementTP);
 24 static void with_grandpa(TREE, position);
 25 
 26 static void insert_node_to_nonempty_tree(TREE, position);
 27 static TREE left_single_rotate(TREE);
 28 static TREE left_double_rotate(TREE);
 29 static TREE right_single_rotate(TREE);
 30 static TREE right_double_rotate(TREE);
 31 static TREE left_zig_zig(TREE);
 32 static TREE right_zig_zig(TREE);
 33 
 34 void main(void) 
 35 {
 36     TREE tr;
 37     tr = NULL;
 38     tr = insert_value(tr, 6);
 39     tr = insert_value(tr, 5);
 40     tr = insert_value(tr, 4);
 41     tr = insert_value(tr, 3);
 42     tr = insert_value(tr, 1); 
 43     tr = insert_value(tr, 2); 
 44 
 45     tr = find_value(tr, 2);
 46     printf("%d\n", tr->rchild->lchild->element);
 47 }
 48 
 49 /* 
 50  * insert a value into the tree
 51  * return root address of the tree
 52  */
 53 position insert_value(TREE tr, ElementTP value) 
 54 {
 55     position np;
 56     /* prepare the node */
 57     np = (position) malloc(sizeof(struct node));
 58     np->element = value;
 59     np->parent  = NULL;
 60     np->lchild  = NULL;
 61     np->rchild  = NULL;
 62  
 63     if (tr == NULL) tr = np;
 64     else {
 65         insert_node_to_nonempty_tree(tr, np);
 66     }
 67     return tr;
 68 }
 69 
 70 
 71 /*
 72  *
 73  * return NUll if not found 
 74  */
 75 TREE find_value(TREE tr, ElementTP value)
 76 {
 77     position np;
 78 
 79     np = search_value(tr, value);
 80     if (np != NULL && np != tr) {
 81         splay_tree(tr, np);
 82     }
 83     return np;
 84 }
 85 
 86 /*
 87  * splaying the tree after search
 88  */
 89 static void splay_tree(TREE tr, position np)
 90 {
 91     while (tr->lchild != np && tr->rchild != np) {
 92         with_grandpa(tr, np);
 93     }
 94     if (tr->lchild == np) {
 95         right_single_rotate(tr);
 96     }
 97     else if (tr->rchild == np) {
 98         left_single_rotate(tr);
 99     }
100 }
101 
102 /*
103  * dealing cases with grandparent node
104  */
105 static void with_grandpa(TREE tr, position np)
106 {
107     position parent, grandPa;
108     int i,j; 
109 
110     parent  = np->parent;
111     grandPa = parent->parent;
112  
113     i = (grandPa->lchild == parent) ? -1 : 1;
114     j = (parent->lchild == np) ? -1 : 1;
115     if (i == -1 && j == 1) {
116         right_double_rotate(grandPa);
117     }
118     else if (i == 1 && j == -1) {
119         left_double_rotate(grandPa);
120     }
121     else if (i == -1 && j == -1) {
122         right_zig_zig(grandPa);
123     }
124     else {
125         left_zig_zig(grandPa);
126     }
127 }
128 
129 /*
130  * search for value
131  */
132 static position search_value(TREE tr, ElementTP value) 
133 {
134     if (tr == NULL) return NULL; 
135 
136     if (tr->element == value) {
137         return tr;
138     }
139     else if (value < tr->element) {
140         return search_value(tr->lchild, value);
141     }
142     else {
143         return search_value(tr->rchild, value);
144     }
145 }
146 
147 /* 
148  * left single rotation 
149  * return the new root
150  */
151 static TREE left_single_rotate(TREE tr) 
152 {
153     TREE newRoot, parent;
154     parent  = tr->parent;
155     newRoot = tr->rchild;
156     /* detach & attach */ 
157     if (newRoot->lchild != NULL) newRoot->lchild->parent = tr;
158     tr->rchild = newRoot->lchild;
159    
160     /* raise new root node */
161     newRoot->lchild = tr;
162     newRoot->parent = parent;
163     if (parent != NULL) {
164         if (parent->lchild == tr) {
165         parent->lchild = newRoot;
166     }
167     else {
168         parent->rchild = newRoot;
169     }
170     }
171     tr->parent = newRoot;
172     return newRoot;
173 }
174 
175 /* 
176  * right single rotation 
177  * return the new root
178  */
179 static TREE right_single_rotate(TREE tr) 
180 {
181     TREE newRoot, parent;
182     parent  = tr->parent;
183     newRoot = tr->lchild;
184 
185     /* detach & attach */
186     if (newRoot->rchild != NULL) newRoot->rchild->parent = tr;
187     tr->lchild = newRoot->rchild;
188   
189     /* raise new root node */
190     newRoot->rchild = tr;
191     newRoot->parent = parent;
192     if (parent != NULL) {
193         if (parent->lchild == tr) {
194         parent->lchild = newRoot;
195     }
196     else {
197         parent->rchild = newRoot;
198     }
199     }
200     tr->parent = newRoot;
201     return newRoot;
202 }
203 
204 /*
205  * left double rotation
206  * return
207  */
208 static TREE left_double_rotate(TREE tr) 
209 {
210     right_single_rotate(tr->rchild);
211     return left_single_rotate(tr);
212 }
213 
214 /*
215  * right double rotation
216  * return
217  */
218 static TREE right_double_rotate(TREE tr) 
219 {
220     left_single_rotate(tr->lchild);
221     return right_single_rotate(tr);
222 }
223 
224 /*
225  * insert a node to a non-empty tree
226  * called by insert_value()
227  */
228 static void insert_node_to_nonempty_tree(TREE tr, position np)
229 {
230     /* insert the node */
231     if(np->element <= tr->element) {
232         if (tr->lchild == NULL) {
233             /* then tr->lchild is the proper place */
234             tr->lchild = np;
235             np->parent = tr;
236             return;
237         }
238         else {
239             insert_node_to_nonempty_tree(tr->lchild, np);
240         }
241     }
242     else if(np->element > tr->element) {
243         if (tr->rchild == NULL) {
244             tr->rchild = np;
245             np->parent = tr;
246             return;
247         }
248         else {
249             insert_node_to_nonempty_tree(tr->rchild, np);
250         }
251     }
252 }
253 
254 /*
255  * right zig-zig operation
256  */
257 static TREE right_zig_zig(TREE tr)
258 {
259     position parent,middle,newRoot;
260     parent  = tr->parent;
261     middle  = tr->lchild;
262     newRoot = tr->lchild->lchild;
263 
264     tr->lchild = middle->rchild;
265     if (middle->rchild != NULL) middle->rchild->parent = tr;
266 
267     middle->rchild = tr;
268     tr->parent     = middle;
269 
270     middle->lchild = newRoot->rchild;
271     if (newRoot->rchild != NULL) newRoot->rchild->parent = middle;
272 
273     newRoot->rchild = middle;
274     middle->parent  = newRoot;
275 
276     newRoot->parent = parent;
277     if (parent != NULL) {
278         if (parent->lchild == tr) {
279         parent->lchild = newRoot;
280     }
281     else {
282         parent->rchild = newRoot;
283     }
284     }
285     return newRoot;  
286 }
287 
288 /*
289  * left zig-zig operation
290  */
291 static TREE left_zig_zig(TREE tr)
292 {
293     position parent,middle,newRoot;
294     parent  = tr->parent;
295     middle  = tr->rchild;
296     newRoot = tr->rchild->rchild;
297 
298     tr->rchild = middle->lchild;
299     if (middle->lchild != NULL) middle->lchild->parent = tr;
300 
301     middle->lchild = tr;
302     tr->parent     = middle;
303 
304     middle->rchild = newRoot->lchild;
305     if (newRoot->lchild != NULL) newRoot->lchild->parent = middle;
306 
307     newRoot->lchild = middle;
308     middle->parent  = newRoot;
309 
310     newRoot->parent = parent;
311     if (parent != NULL) {
312         if (parent->rchild == tr) {
313         parent->rchild = newRoot;
314     }
315     else {
316         parent->lchild = newRoot;
317     }
318     }
319     return newRoot;  
320 }

posted @ 2016-08-12 21:59 Penn000 阅读(204) 评论(0) 编辑收藏举报

刷新页面返回顶部

Penn000

每一个不曾起舞的日子，都是对生命的辜负

伸展树(splay)

伸展树的C实现

公告