某 dp 题单题解 0116
1 甲虫
Problem
给定一个数轴,现在有一只甲虫在原点。有 \(n\) 滴露水,坐标分别为 \(x_1,x_2,\dots,x_n\),每滴露水有 \(m\) 的价值。甲虫每秒可以移动一步,它在 \(t\) 时刻所能获得的露水的价值为 \(\max(m-t,0)\)。求甲虫最多能喝到多少水。
\(0\le n\le 300,1\le m\le 10^6,|x_i|\le 10^4\),保证 \(x_i\) 互不相同。
时空限制:4s,15.63MB。
Sol
经典的区间 dp。考虑 \(f_{i,j,0/1}\) 表示吃完 \([i,j]\) 的露水,在 \(i/j\) 的最大值。然后发现这东西还要考虑时间,类似于 ABC219H,考虑费用提前计算。这样的话还要枚举吃多少露水,答案转移时更新即可。
不能单独记录一个 \(g_{i,j,0/1}\) 的原因是可能存在一段 \([i,j]\) 的最优策略花的时间更长,却需要尽快的去取旁边的露水,就是这个 \(g\) 只保证了局部的最优性,所以是错的。
时间复杂度:\(\mathcal{O}(n^3)\)。
code
#include<bits/stdc++.h>
using namespace std;
#define Fin(file) freopen(file,"r",stdin)
#define Fout(file) freopen(file,"w",stdout)
#define L(i,j,k) for(int i=(j);i<=(k);++i)
#define R(i,j,k) for(int i=(j);i>=(k);--i)
#define ll long long
int n,m;
int a[310];
ll f[310][310][2];
int main(){
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m;
ll ans=0;
L(i,1,n)cin>>a[i];
sort(a+1,a+n+1);
L(len,1,n){
memset(f,0,sizeof(f));
L(i,1,n)ans=max(ans,f[i][i][0]=f[i][i][1]=m-abs(a[i])*len);
L(i,2,len)L(l,1,n-i+1){
int r=l+i-1,tmp=len-r+l;
f[l][r][0]=max(f[l+1][r][0]-abs(a[l+1]-a[l])*tmp,f[l+1][r][1]-abs(a[r]-a[l])*tmp)+m;
f[l][r][1]=max(f[l][r-1][0]-abs(a[r]-a[l])*tmp,f[l][r-1][1]-abs(a[r]-a[r-1])*tmp)+m;
ans=max(ans,max(f[l][r][0],f[l][r][1]));
}
}
cout<<ans<<"\n";
return 0;
}
2 粉刷匠
Problem
有 \(n\) 条木板,每条木板有 \(m\) 个格子,每个格子需要被涂成红色或蓝色,初始时没有颜色。每次操作可以给一条木板的某一段连续的格子上色,同一个格子不能被多次上色。如果只能操作 \(T\) 次,求最多能正确粉刷的格子数量。
\(1\le n,m\le 50,0\le T\le 2500\)。
时空限制:1s,125MB。
Sol
发现每一条木板之间互不影响,于是先只考虑一条木板。
定义 \(f_{i,j}\) 表示前 \(i\) 个格子,操作 \(j(j>0)\) 次的最大数量。则有 \(f_{i,j}=\max\limits_{k<i}(f_{i-1,j},f_{k,j-1}+\max(cnt(k+1,i,0),cnt(k+1,i,1)))\),其中 \(cnt(l,r,v)\) 表示 \([l,r]\) 中,\(v\) 出现了多少次。这里,红色和蓝色分别对应 \(0/1\)。
然后多条木板的话就很简单了,再上一个背包就行了。记 \(v_{i,j}\) 表示第 \(i\) 条木板操作 \(j\) 次的最大数量,\(g_{i,j}\) 表示前 \(i\) 条木板操作 \(j\) 次的最大数量。则有 \(g_{i,j}=\max\limits_{k<j}\{g_{i-1,k}+v_{i,j-k}\}\)。显然操作次数越多越好,所以最后答案就是 \(g_{n,T}\)。
若将 \(n,m\) 视为同级,则时间复杂度为 \(\mathcal{O}(n^4)\)。
Code
#include<bits/stdc++.h>
using namespace std;
#define Fin(file) freopen(file,"r",stdin)
#define Fout(file) freopen(file,"w",stdout)
#define L(i,j,k) for(int i=(j);i<=(k);++i)
#define R(i,j,k) for(int i=(j);i>=(k);--i)
int n,m,c;
int a[55][55],s[55][55],f[55][55],g[55][2510],h[55][55];
int main(){
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m>>c;
L(i,1,n)L(j,1,m){
char c;cin>>c;
a[i][j]=c-'0';
s[i][j]=a[i][j]+s[i][j-1];
}
L(x,1,n){
memset(f,0,sizeof(f));
f[1][1]=1;
L(i,2,m)L(j,1,i)L(k,0,i-1){
int v=s[x][i]-s[x][k];
if(!a[x][i])v=i-k-v;
f[i][j]=max(f[i][j],f[k][j-1]+v);
}
L(i,1,m)L(j,i,m)h[x][i]=max(h[x][i],f[j][i]);
}
L(i,1,n)L(j,1,min(i*m,c))L(x,0,min(j,m))g[i][j]=max(g[i][j],g[i-1][j-x]+h[i][x]);
int ans=0;
L(i,1,c)ans=max(ans,g[n][i]);
cout<<ans<<"\n";
return 0;
}
3 Don't Be a Subsequence
Problem
输入一个只有小写字母构成的字符串 \(S\),求不是它的子序列的最短串。如果有多个,输出字典序最小的。
\(1\le |S|\le 2\times 10^5\)。
时空限制:2s,256MB。
Sol
定义 \(f_i\) 表示只考虑前 \(i\) 个时最短串的长度。则有 \(f_i=1+\min\limits_{c=0}^{25}\{ f_{pre_{i,c}-1}\}\),\(pre_{i,c}\) 表示第 \(i\) 个位置之前的最靠后的是 \(c\) 的位置,这里的 \(c\) 指的是 第几个小写字母。
但是这个题还要求字典序最小,如果把 \(f\) 数组变为 string 的话是会 MLE 的,于是就只能枚举 \(T\) 的第 \(i\) 位能否取某一个字符的话,但这个并不好判断,因为不知道取 \(i\) 的时候能否取到最短。所以这个时候倒序 dp 就很显然了,令 \(f_{i}\) 表示只考虑后 \(i\) 个时最短串的长度,则有 \(f_{i}=1+\min\limits_{c=0}^{25}\{f_{nxt_{i,c}+1}\}\)。方案反过来求就行了,这个可以通过逆推得到。
时空复杂度:\(\mathcal{O}(n|\Sigma|)\),\(|\Sigma|\) 表示字符集大小,这里是 \(26\)。
Code
#include<bits/stdc++.h>
using namespace std;
#define Fin(file) freopen(file,"r",stdin)
#define Fout(file) freopen(file,"w",stdout)
#define L(i,j,k) for(int i=(j);i<=(k);++i)
#define R(i,j,k) for(int i=(j);i>=(k);--i)
int n;
int f[200010],nxt[200010][26];
string s;
int main(){
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>s;n=s.size();
s=" "+s;
R(i,n,1)L(j,0,25)nxt[i][j]=(s[i]-'a'==j)?i:nxt[i+1][j];
memset(f,0x3f,sizeof(f));
f[n+1]=1;
R(i,n,1)L(j,0,25)if(!nxt[i][j])f[i]=1;else f[i]=min(f[i],f[nxt[i][j]+1]+1);
int now=1,ans=f[1];
while(ans>1){
L(i,0,25)if(f[now]==f[nxt[now][i]+1]+1){
cout<<(char)(i+'a');
now=nxt[now][i]+1;
break;
}
--ans;
}
L(i,0,25)if(!nxt[now][i]){cout<<(char)(i+'a');break;}
cout<<"\n";
return 0;
}
4 Ribbons on Tree
Sol
Code
E. Yes or No
Problem
有 \(n + m\) 个问题,其中有 \(n\) 个问题的答案是 Yes,有 \(m\) 个问题的答案是 No。每次只有回答完一个问题后才能知道这个问题的答案,求最优策略下期望对多少,答案对质数 \(P\) 取模。
\(1\le n, m\le 5\times 10^5\)。
时空限制:2s,256MB。
Sol
先考虑一个 \(\mathcal{O}(n^2)\) 的 dp:记 \(f_{i, j}\) 表示猜了 \(i + j\) 个问题,其中有 \(i\) 个问题的答案是 Yes 的最优期望。
转移显然:
因为剩下的问题中如果 Yes 的数量 \(\ge\) No 的数量,肯定就选 Yes,否则选 No。
发现这个过程很像走折线,可以向组合数的方向考虑。
这里借用一张图:
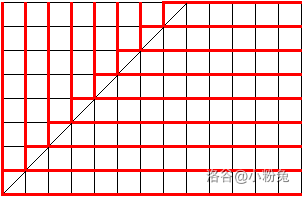
若令左下角为最终答案,对于折线图上的 \((i, j)\) 显然是只能像 左 / 下走(可以发现图中的每一个点 \((i, j)\) 向 左 / 下 的线只有一条,当 \(i \neq j\) 的时候显然路径唯一,方向与 \(i, j\) 的大小关系有关,对于 \(i = j\) 的情况,我们可以钦定向左),那么每次猜的答案显然是确定的,所以最终的答案也可以表示为一条折线,那么最终的期望就等于 所有答案红线与图中红线的方向相同 的段数 再除以总的方案数,总方案数显然为 \(\binom{n + m}{m}\)。但是这个走势相同的次数要对每一个 \(i\) 单独求,比较麻烦。发现麻烦的原因是不知道答案折线在 \(x = i\) 的时候的位置是位于斜线的上方还是下方。
那么我们可以考虑强制将某一个部分的强行翻折以便于统计,此时不妨令 \(n\ge m\),则可以把斜线上方的翻折下来,考虑此时的统计的信息是否会有变化,发现只有在 \((i, i)\) 处的点的连出去的线的选择状态会发生改变,于是统计 经过 \((i, i)\) 的 恰好向左走的 答案折线数量 即可,表示出来即为 \(\sum\limits_{i = 1}^{m}F(i - 1, i)\times F(n - i, m - i)\)。其中 \(F(i, j)\) 表示 \((0, 0) \to (i, j)\) 只向 上 / 右 走的方案数之和,即为 \(\binom{i + j}{i}\),即选 \(i\) 条竖着的直线在第几根,后面的 \(F(n - i, m - i)\) 指的是 \((i, j)\to (n, m)\) 的方案数,和上一个差不多。
Code
#include<bits/stdc++.h>
#define ll long long
#define sz(a) ((int) (a).size())
#define vi vector < int >
#define pb emplace_back
using namespace std;
const int mod = 998244353;
int n, m;
ll fac[1000010], ifac[1000010], inv[1000010];
ll binom(int n, int m) {
if(n < 0 || m < 0 || n < m)
return 0;
return fac[n] * ifac[m] % mod * ifac[n - m] % mod;
}
ll power(ll a, int b) {
ll res = 1;
for(; b; b >>= 1, a = a * a % mod)
if(b & 1)
res = res * a % mod;
return res;
}
ll calc(int x, int y) {
return binom(x + y, x);
}
int main() {
ios :: sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> n >> m;
if(n < m)
swap(n, m);
fac[0] = fac[1] = ifac[0] = ifac[1] = inv[1] = 1;
for(int i = 2; i <= n + m; ++i)
fac[i] = fac[i - 1] * i % mod, inv[i] = (mod - mod / i) * inv[mod % i] % mod, ifac[i] = ifac[i - 1] * inv[i] % mod;
ll ans = 0;
for(int i = 1; i <= m; ++i)
(ans += calc(i - 1, i) * calc(n - i, m - i)) %= mod;
ans = ans * power(calc(n, m) % mod, mod - 2) % mod;
cout << n + ans << "\n";
return 0;
}

