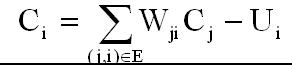神经网络 （codevs 1088） 题解

【问题描述】

    人工神经网络（Artificial Neural Network）是一种新兴的具有自我学习能力的计算系统，在模式识别、函数逼近及贷款风险评估等诸多领域有广泛的应用。对神经网络的研究一直是当今的热门方向，兰兰同学在自学了一本神经网络的入门书籍后，提出了一个简化模型，他希望你能帮助他用程序检验这个神经网络模型的实用性。

    在兰兰的模型中，神经网络就是一张有向图，图中的节点称为神经元，而且两个神经元之间至多有一条边相连，下图是一个神经元的例子：神经元〔编号为1）

   图中，X1—X3是信息输入渠道，Y1－Y2是信息输出渠道，C1表示神经元目前的状态，Ui是阈值，可视为神经元的一个内在参数。神经元按一定的顺序排列，构成整个神经网络。在兰兰的模型之中，神经网络中的神经元分为几层；称为输入层、输出层，和若干个中间层。每层神经元只向下一层的神经元输出信息，只从上一层神经元接受信息。上图是一个简单的三层神经网络的例子。兰兰规定，Ci服从公式：（其中n是网络中所有神经元的数目）

公式中的Wji（可能为负值）表示连接j号神经元和 i号神经元的边的权值。当 Ci大于0时，该神经元处于兴奋状态，否则就处于平静状态。当神经元处于兴奋状态时，下一秒它会向其他神经元传送信号，信号的强度为Ci。如此．在输入层神经元被激发之后，整个网络系统就在信息传输的推动下进行运作。现在，给定一个神经网络，及当前输入层神经元的状态（Ci），要求你的程序运算出最后网络输出层的状态。

【样例输入】

    5 6

    1 0

    1 0

    0 1

    0 1

    0 1

    1 3 1

    1 4 1

    1 5 1

    2 3 1

    2 4 1 

    2 5 1

【样例输出】 

    3 1

    4 1

    5 1

【解题思路】

     本题为NOIP2003提高组第一题，看了很多题解，包括官方给出的该题考查的知识点，很多都写着拓扑排序，为什么我没用拓扑排序呢？（我不会告诉你们我对拓扑排序还不熟练的）其实这道题完全不需要用拓扑排序，直接一个简单的搜索（或者叫枚举）就够了，不用剪枝，不用递归，不用回溯，直接从1开始把所有点搜一遍，然后把输出层的点记录下来。计算公式的时候有几个很关键的地方，最后的Ui只要减一次，因为∑后面-Ui没有打括号……被坑了一次（如果只减了一次Ui，恭喜你，得20分）……还有就是输入层不需要减Ui（如果没减，恭喜你，得40分），其次就是对于最后的输出层的点如果它的C值小于0应当做0处理（如果处理了，当年的省一到手），最后一个最坑的也是最难以引人注目的但是在问题描述中摆在最起眼的位置，同时也是得满分最关键的一点就是：只有Ci大于0的才会往下传……（本人这里没注意少了20分）下面上程序。

【代码实现】

var a:array[1..200,1..200] of longint;
    i,j,n,p,q,w:longint;
    f:array[1..200] of boolean;
    c,u:array[1..200] of longint;
    flag:boolean;
    b:array[1..200] of longint;
begin
 fillchar(f,sizeof(f),true);
 readln(n,p);
 for i:=1 to n do
  readln(c[i],u[i]);
 for i:=1 to n do
  for j:=1 to n do
   a[i,j]:=-maxint;
 for i:=1 to p do
  begin
   read(q,w);
   read(a[q,w]);
  end;
 for i:=1 to n do
  begin
   flag:=true;
   for j:=1 to n do
    if a[j,i]<>-maxint then
     if c[j]>0 then//大于0的才会往下传
      begin
       flag:=false;
       f[j]:=false;
       c[i]:=c[i]+a[j,i]*c[j];
      end;
   if not flag then//输出层不要-Ui，同时只要减一次Ui
    c[i]:=c[i]-u[i];
  end;
 w:=0;flag:=true;
 for i:=1 to n do
  if f[i] then
   begin
    inc(w);
    b[w]:=i;
    if c[i]>0 then
     flag:=false;
   end;
 if flag then
  writeln('NULL')
 else
  for i:=1 to w do
   if c[b[i]]>0 then//大于0的才要输出
    writeln(b[i],' ',c[b[i]]);
end.