联考题解
24/9/27
龙(dragon)#
难点:
(1)删边后如何寻找新的最短路。
(2)A,B两方的决策互相影响十分复杂。
(3)如何统计每个起点的ans。
解题:
(3)解决这类多起点一终点的问题,可以想到dp。
(1)解决这类最短路转移的问题,可以考虑最短路树。
(2)解决这类博弈问题,可以设计两个dp数组,分别维护影响前后的ans,在转移到最终的答案数组。
24/9/26
拆除炸弹(youyou)#
难点:
(1)如何维护与判断一个二分图(没有奇环)。
(2)维护一个区间并要将其排序,时间复杂度大。
(3)区间内含有的信息量过大。
解题:
(1)判断二分图,可以用并查集。
(2)需要维护并排序区间,可以用线段树,但要注意信息量与合并复杂度。
(3)对于这类问题,可以:1.对部分信息记忆化并离线改变区间的查询顺序。2.分析性质去掉无用信息。
(3‘)关于并查集(树)的连通性问题,只有n-1条树边起关键作用。
赖教(lai)#
难点:
(1)“赖教”势力的扩散不好处理。
(2)使最终的“赖教”消失难维护。
(3)如何使军队花费最优。
解题:
(1)对于这类会扩散的问题,可以逆思考空区间的缩减,并将其绘成形如等腰三角的图。
(2)使最终无法扩散,即"赖教"消失,会发现就是诸多等腰三角形的拼接清空完1到n。
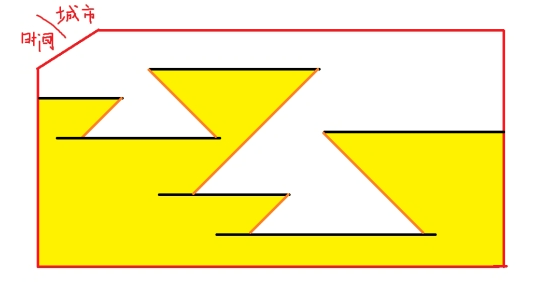
(3)区间覆盖的最优性问题,可以考虑最短路算法(以区间为点的点去最短路)。
(3‘)点权最短路寻找出度困难时,可以使用线段树维护出度,暴力log查,由于是点权最短路(第一次入队即最优),所以查询后就删除,保证时间复杂度。
24/10/8
交换(swap)#
难点:
(1)题目的转化。
(2)拓扑序计数。
(3)对于序列上,有关多组偏序关系统计的方案数(例:序列上要求一些(a_i< a_j)一些(a_i > a_j))。
解题:
(1)先将某个值的位置交换转化为点之间的连边,序列变图论问题。
(2)这是一个NP问题,完全没法做,所以再次转话题意,发现每个点只会与相邻的两点连边,所以图论再变序列问题。
(3)dp的设计需维护排名,二维状态表示考虑了前i位,i的排名为j。每次转移即为在前i个数的序列中插入一个新的数,再考虑排名变化和与i-1的偏序关系。
匹配子串(brackets)#
难点:
(1)“?”难处理,合法的括号区间难处理。
(2)多个条件限制难维护。
(3)区间查询困难。
解题:
(1)合法括号序列的充要条件为:
1.对于所有前缀, ( 和 ? 的总数大于等于 ) 的数量。
2.对于所有后缀, ) 和 ? 的总数大于等于 ( 的数量。
3.长度为偶数。
(2 )扫描线+线段树,扫描线在 i 的时候给 a_i 加 1 ,在 f_i 的时候给 a_i 减一。对于右端点为i的合法区间数即为\sum\limits_{j=g_i}^{i}a_j,用线段树维护单点加和区间查就行了。
(3)我们将区间权值放在左端点上(即维护左端点为i的合法区间数),即将之前的区间查改为区间加,每次查询就查区间和就行了。但因为要查区间内所有合法子区间,所以要历史版本和。
24/10/7
图(graph)#
难点:
(1)连通块之间的连边和起始边数分讨复杂。
(2)连通块的大小奇偶性分讨复杂。
(3)必胜策略难找。
解题:
(1)考虑最终状态,\dfrac{n(n−1)}{2}-m − k(n − k),k与n-k表示最终剩下的两个连通块的大小。
对于这种过程复杂的题目,可以从最终状态出发倒着考虑。
(2)只需维护最终两个连通块的奇偶性就行了,就是将所有两个连通块分为两个集合(1与n分别位于不同集合)。
(3)必胜策略其中一种原因是,先手总是可以完全抵消后手的操作并控制最终结果





【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 为DeepSeek添加本地知识库
· 精选4款基于.NET开源、功能强大的通讯调试工具
· DeepSeek智能编程
· 大模型工具KTransformer的安装
· [计算机/硬件/GPU] 显卡