算法描述》关于二分的两三事
关于二分
二分,是一种流氓算法,这种方法适用于直接算(猜、蒙、试)答案,然后直接得出最优解,
这一方法,对于可以轻易证明答案是否可行(o(n)、o(1))的题目有奇效,
(在NOIP2015考试的时候出了这么一道题,放倒一推蒟蒻(包括我))
二分的使用条件
1.如上文所说,对于轻易证明答案是否可行的题目有奇效,来一道解决一道,对于子问题有这一性质的,也可以同样用这种方法解决,奇效。(以下有相关内容)
2.对于所查询区间值为递增或递减的问题来说,这也是一种极其可行的方法,
关于写法以及STL若干事
每一位神犇几乎都有自己有个性的二分写法,因为这个东西可以有所差异的地方实在太多,但究其本身,还都是同一种道理。
1.关于<algorithm>中,STL的写法
在c++的库函数里,有两个二分函数,分别叫upper_bound和lower_bound。
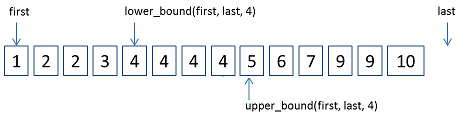
upper_bound
这一库函数的定义是:在当前传来的非降序列两个地址中间,return第一个大于当前传来的值的地址。
使用格式为:upper_bound(a+1,a+n+1,num);
其中a数组为我们所要查询的非降数组,而1、n+1分别为我们要查找的区间地址(也即数组变量名+查询的开始 / 结束位置),num为我们所要查询的值。
具体库函数代码如下
1 int upper_bound(int *array, int size, int key) 2 { 3 int first = 0, len = size-1; 4 int half, middle; 5 6 while(len > 0){ 7 half = len >> 1; 8 middle = first + half; 9 if(array[middle] > key) //中位数大于key,在包含last的左半边序列中查找。 10 len = half; 11 else{ 12 first = middle + 1; //中位数小于等于key,在右半边序列中查找。 13 len = len - half - 1; 14 } 15 } 16 return first; 17 }
lower_bound
这一库函数的定义是:在当前传来的非降序列两个地址间,return第一个大于等于当前传来的值的地址。
使用格式:lower_bound(a+1,a+n+1,num);
各数组意义的定义和上面的基本一致
库函数代码如下
1 int lower_bound(int *array, int size, int key) 2 { 3 int first = 0, middle; 4 int half, len; 5 len = size; 6 7 while(len > 0) { 8 half = len >> 1; 9 middle = first + half; 10 if(array[middle] < key) { 11 first = middle + 1; 12 len = len-half-1; //在右边子序列中查找 13 } 14 else 15 len = half; //在左边子序列(包含middle)中查找 16 } 17 return first; 18 }
2.关于个人代码习惯
这里有两种,分别是preyW和szl两神犇的不同二分写法习惯,在这里供参考
1 int prey_BS(int l, int r, int key) 2 { 3 while( l < r - 1 ) 4 { 5 m = (l+r)>>1; 6 if(a[m] < key) 7 l = m + 1; 8 else 9 r = m; 10 } 11 return l; 12 }
1 int zl_BS(int l, int r, int key) 2 { 3 int ans; 4 while(l < = r) 5 { 6 m = (l + r)>>1; 7 if(a[m] < key) 8 l = middle + 1; 9 else{ 10 r = m - 1; 11 ans = r; 12 } 13 } 14 return ans; 15 }
这两种方法可能和神犇亲手写的有出入,不过大概就是这样
总的来说,二分还是一种解题利器,如果对于写法不够明确的看官,可以用以上的STL以及神犇写法来代替自己原本的,可能效果会更好
然后例题就是全部openjudge以及codevs的二分题
祝大家刷的开心




