算法技巧讲解》关于对于递推形DP的前缀和优化
这是在2016在长沙集训的第三天,一位学长讲解了“前缀和优化”这一技巧,并且他这一方法用的很6,个人觉得很有学习的必要。
这一技巧能使线性递推形DP的速度有着飞跃性的提升,从O(N2)优化到O(N)也不是不可能。
这一技巧的主要思想是使要加和的数据完全储存,并且在下一次计算中直接调用,所以你的对于DP当前项的查询无论是N还是logN,这一方法都能直接解决。
以一道题来作为我们的例子;
openjudge9277 (cf 295D跟这题差不多,只是对比于这道题要加个高度,但不用优化)
分享出题目
9277:Logs Stacking堆木头
- 总时间限制: 1000ms
- 内存限制: 131072kB
- 描述
-
Daxinganling produces a lot of timber. Before loading onto trains, the timberjacks will place the logs to some place in the open air first. Looking from the sideway, the figure of a logs stack is as follows:
We have known that the number of logs in each layer is fewer than the lower layer for at least one log, and that in each layer the logs are connected in a line. In the figure above, there are 12 logs in the bottom layer of the stack. Now, given the number of logs in the bottom layer, the timberjacks want to know how many possible figures there may be.
给出在最底层的木头的个数,问有多少种堆放木头的方式,当然你的堆放方式不能让木头掉下来.
在堆放的时候木头必须互相挨着在一起. - 输入
-
The first line of input contains the number of test cases T (1 <= T <= 1000000). Then T lines follow. Every line only contains a number n (1 <= n <= 200000) representing the number of logs in the bottom layer.
- 输出
-
For each test case in the input, you should output the corresponding number of possible figures. Because the number may be very large, just output the number mod 10^5.
- 样例输入
-
4 1 2 3 5 - 样例输出
-
1 2 5 34 - 提示
-
当输入3时,有5种方式
第一种:上面一个也不放
第二种:上面放一根,放在最左边
第三种:上面放一根,放在最右边
第四种:上面放二根
第五种:上面先放二根,然后在二根的上面放一根那么对于这样一道比较裸的递推题,只要理解题意,推推样例画画图即可得动态转移方程:
![]()
但是,这道题的数据范围是20w,直接n2递推肯定过不了,所以我们通过计算前缀和可以得到一个更优的方法。
我们先来判断一下每一组答案是怎么来的
f[i]=f[i-1]*1+f[i-2]*2+f[i-3]*3+.....+f[1]*(i-1)
f[i+1]=f[i]*1+f[i-1]*2+f[i-2]*3+.......+f[1]*i
我们发现,f[i+1]只是在f[i]的基础上加了一组f[1]到f[i]的和,通过动态维护这一个和的结果,我们可以O(1)得出当前解。
所以现在只用考虑动态维护就好
来看张图
![]()
我们用f数组来计算当前解,用s数组来计算前缀和,这样就可以轻易的得出解啦
所以,在一般考试遇到这种题的时候,正常人花一定的时间都能算出简单的递推式,那么出题人也不傻,数据量会给的比较大,所以,这种前缀和优化就变得至关重要。决定了你究竟是那AC还是只拿暴力分。
下面给出代码
![]() View Code
View Code1 #include<stdio.h> 2 int f[230000],s,T,n; 3 int main() 4 { 5 int i,j; 6 f[1]=1,f[2]=2,s=1; 7 for(i=3;i<=200000;++i) 8 { 9 s+=f[i-1]; 10 s%=100000; 11 f[i]+=f[i-1]+s; 12 f[i]%=100000; 13 } 14 scanf("%d",&T); 15 while(T--) 16 { 17 scanf("%d",&n); 18 printf("%d\n",f[n]); 19 } 20 return 0; 21 }


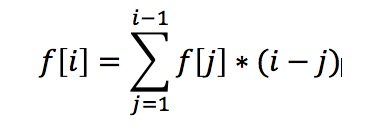




 浙公网安备 33010602011771号
浙公网安备 33010602011771号