数据结构》关于线段树两三事(新手向)(工具向)
今天我们来安利线段树,这个东西一段时间不写的话就很容易忘(@可能看到这篇博客的某人),这是一个关于O(logn)级别的更改与查询(期望)的数据结构,
那么,对于线段树的裸题,有多种,分为(1.区间修改区间查询,2.单点修改区间查询,3.区间修改单点查询)(问我怎么没有单点修改单点查询的,请自裁)
但总而言之,线段树分为查询与修改两种操作。
那么现在我们来说说线段树的基本结构。
首先,对于基本的单点修改与查询来说,我们的数组定义一般就只有题目数据大小(O(m)),但是对于线段树来说,因为线段树从结构来看是一颗二叉树,如果你写的好,理想化空间只需要O(2m-1),但是对于一般的裸题与模板(与习惯),我们要开4倍空间,原因下面的(关于线段树空间与时间复杂度)会讲。
那么首先,我们来看一张关于线段树的图片。
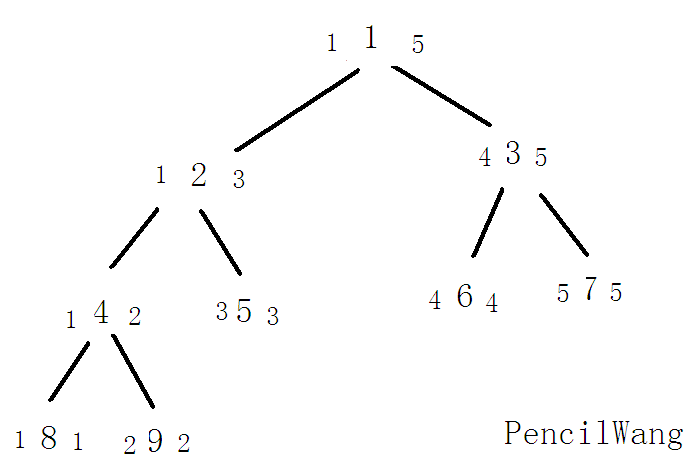
那么很明显,既然我们现在研究的数据结构叫线段树,那么无疑它是树形结构的,那么对于每个线段树的每个点,他都有三个基本数据,分别是当前点左边开头节点元素坐标、右边结尾节点元素坐标、以及我们要求的从左起始点到右结尾点的一个我们所需的值(可以是求和、可以是平均值、可以是最大值)。
那么对于线段树这种数据结构,如上图,上图中每三个数字为一组,中间的数字代表这个元素在数组上的位置,左边的1和右边的5分别代表我们当前记录的这个我们所需的值是从哪个区间求来的(例如最上面的1 1 5代表这个元素在数组位置是1,记录某个我们所需要的值是从1到5取得的)。
那么接下来,因为线段树是二叉树,我们分开左节点和右节点的方法为:假设当前节点元素位置为K,左起始点为L,右结尾点为R,然后先算出一个(L+R)/2,作为一个中间值,然后当前节点的左儿子的数组位置就为K*2,起始点坐标和父亲一样是L,而结尾坐标则是中间值,而右儿子的数组坐标就为K*2+1,起始节点坐标就为中间值+1,结尾点坐标就为R。那么如果当前坐标左起始节点等于了右终止节点,那么就说明我们找到了一个叶子节点,直接在叶子节点上赋值就可以了,当然如果这个节点不是叶节点,那么就要同时加上左子树和右子树的值了,这是一个递归的过程。
到这里,想必建这棵线段树的方法大家都知道了(不清楚可以结合代码理解),下面就华丽的贴出代码:

1 void bulid_tree_sum(int K,int L,int R)//K表示该节点的下标值,L、R分别表示区间的左右端点 2 { 3 if(L==R) 4 { 5 cin>>tree_sum[K]; 6 return ; 7 } 8 9 int mid=(L+R)>>1; 10 11 build_tree_sum(K<<1,L,mid);//建立左儿子 12 build_tree_sum(K<<1|1,mid+1,R);//建立右儿子 13 14 tree_sum[K]=tree_sum[K<<1]+tree_sum[K<<1|1];//更新父亲节点 15 }
关于修改
修改其实就是改变你某个(或某段)位置上,基本元素的大小,对于不同的题目,就有不同的递归搜索返回值的方式,例如为了做区间修改和区间查询,我们需要一个标记数组,所以在返回的时候不知要改变这棵树原来的每点数值大小,还要做一个标记数组,如果理解了上面的建树,这里应该很好以理解,就是:如果当前查询点的左端点以及右端点在所需要修改区间内就可以完全对于当前节点做修改,不然就选择继续选择查询左子树或右子树。那么下面华丽的贴出代码。

1 void update(int k,int l,int r,int pos,int val) 2 { 3 if(l==r&&l==pos) 4 { 5 tree_sum[k]=val; 6 return ; 7 } 8 9 int mid=(l+r)>>1; 10 11 if(pos<=mid) 12 update(root<<1,l,mid,pos,val); 13 else 14 update(k<<1|1,mid+1,r,pos,val); 15 tree_sum[k]=tree_sum[k<<1]+tree_sum[k<<1|1]; 16 }
关于查询
查询应该是最简单的一步,我们只需要按照题目每个问题所给的区间,来求我们在修改操作里已经做过的操作的结果就行了。也是按照区间,查询当前端点是否完全包括,是就得出值,不是就继续向有关的儿子节点查找。然后直接华丽的贴出代码。

1 int query(int k,int l,int r,int L,int R) 2 { 3 if(L<=l&&r<=R) 4 { 5 return tree_sum[k]; 6 } 7 8 int mid=(l+r)>>1,sum=0; 9 10 if(L<=mid) 11 sum+=query(k<<1,l,mid,L,R); 12 if(mid<R) 13 sum+=query(k<<1|1,mid+1,r,L,R); 14 return sum; 15 }
关于线段树的时间与空间复杂度
关于时间复杂度,应该是比较容易的,因为每个节点的两个子节点,都被强制分为两个大小相差小于等于1的两个,所以基本可以判断,线段树不论是查询还是搜索,它的复杂度都是O(logn)的。
关于空间复杂度,其实看上面的图我们不难发现,即使我们的线段树是颗满二叉树,叶节点为m,那最多节点数量也在2m-1的范围内,但是为什么很多人在写的过程中要开4倍空间才能不CE捏。原因很简单,因为如果你的程序对于每次深搜的结束判断很糟糕的话,那么就是说,你即使对于叶节点也判断为有两个子节点的地址,这时候你再向下去搜,那当然不开4倍就会炸。






