2019-08-12 纪中NOIP模拟B组
T1 [JZOJ4879] 少女觉
题目描述
“在幽暗的地灵殿中,居住着一位少女,名为古明地觉。”
“据说,从来没有人敢踏入过那座地灵殿,因为人们恐惧于觉一族拥有的能力——读心。”
“掌控人心者,可控天下。”
人的记忆可以被描述为一个黑块 $B$ 与白块 $W$ 的序列,其中情感值被定义为序列中黑块数量与白块数量之比。
小五口在发动读心术时,首先要解析人的记忆序列,因此,需要将序列分割为一些段,并且要求每一段记忆序列的情感值都相等。
下面给出两个例子:
BWWWBB -> BW + WWBB $(Ratio=1:1)$
WWWBBBWWWWWWWWWB -> WWWB + BBWWWWWW + WWWB $(Ratio=3:1)$
现在小五手上有一个人的记忆序列,她想要知道,如何将手中的记忆序列分成尽可能多的段呢?
数据范围
对于 $10 \%$ 的数据,$N \leq 15$
对于 $20 \%$ 的数据,$N \leq 500$
另有 $30 \%$ 的数据,$K=1$
另有 $30 \%$ 的数据,$K \leq 50$
对于 $100 \%$ 的数据,$N \leq 10^5$,序列长度不超过 $10^9$
分析
显然每段序列的黑白块之比都等于总序列的黑白块之比
所以只要在每加入一段相同颜色的连续方块时,判断是否能组成一段新的合法序列

#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> using namespace std; #define ll long long #define inf 0x3f3f3f3f #define N 100005 int T, n, ans; int s[N][2], sum[2], last[2]; char c; int gcd(int a,int b) { return !b ? a : gcd(b, a % b); } int main() { freopen("silly.in", "r", stdin); freopen("silly.out", "w", stdout); scanf("%d", &T); while (T--) { ans = sum[0] = sum[1] = last[0] = last[1] = 0; scanf("%d", &n); for (int i = 1; i <= n; i++) { scanf("%d %c", &s[i][1], &c); if (c == 'B') s[i][0] = 0, sum[0] += s[i][1]; if (c == 'W') s[i][0] = 1, sum[1] += s[i][1]; } if (!sum[0]) {printf("%d\n", sum[1]); continue;} if (!sum[1]) {printf("%d\n", sum[0]); continue;} int g = gcd(sum[0], sum[1]); sum[0] /= g; sum[1] /= g; for (int i = 1; i <= n; i++) { int now = s[i][0]; if (!last[now ^ 1] || last[now ^ 1] % sum[now ^ 1]) { last[now] += s[i][1]; continue; } int need = last[now ^ 1] / sum[now ^ 1] * sum[now] - last[now]; if (need < 0) last[now] += s[i][1]; else if (s[i][1] < need) last[now] += s[i][1]; else last[now] = s[i][1] - need, last[now ^ 1] = 0, ans++; } printf("%d\n", ans); } return 0; }
T2 [JZOJ4883] 灵知的太阳信仰
题目描述
“在炽热的核熔炉中,居住着一位少女,名为灵乌路空。”
“据说,从来没有人敢踏入过那个熔炉,因为人们畏缩于空所持有的力量——核能。”
“核焰,可融真金。”
每次核融的时候,空都会选取一些原子,排成一列。然后,她会将原子序列分成一些段,并将每段进行一次核融。
一个原子有两个属性:质子数和中子数。
每一段需要满足以下条件:
1. 同种元素会发生相互排斥,因此,同一段中不能存在两个质子数相同的原子。
2. 核融时,空需要对一段原子加以防护,防护罩的数值等于这段中最大的中子数。换句话说,如果这段原子的中子数最大为 $x$,那么空需要付出 $x$ 的代价建立防护罩。求核融整个原子序列的最小代价和。
数据范围
对于 $20\%$ 的数据,$1 \leq N \leq 100$
对于 $40\%$ 的数据,$1 \leq N \leq 1000$
对于 $100\%$ 的数据,$1 \leq N \leq 10^5$
分析
考场上的想法是记录每个数作为区间末端时可以达到的区间最前端,用 $ST$ 表维护区间最大值,然后在可行范围内枚举断点 $DP$ 得到答案
这样的做法是 $O(n^2)$ 的,所以考虑在枚举断点时如何优化
我们发现每个位置的 $f$ 值只可能从中子数大于等于自身的位置的前一个原子或者是可以达到的最前端位置的前一个原子处转移过来,所以可以维护一个中子数非严格递减的单调队列,将队列中的每个位置对应的答案放入 $set$ 中,这样就便于插入删除元素和查找最小值,操作时间复杂度 $O(log \; n)$

#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <set> using namespace std; #define ll long long #define inf 0x3f3f3f3f #define N 100005 int n, l = 1, r = 0; int a[N], b[N], pos[N], pre[N]; int f[N], q[N], p[N]; multiset<int> s; int main() { freopen("array.in", "r", stdin); freopen("array.out", "w", stdout); scanf("%d", &n); for (int i = 1; i <= n; i++) { scanf("%d%d", a + i, b + i); pre[i] = max(pre[i - 1], pos[a[i]] + 1); pos[a[i]] = i; } memset(f, 0x3f, sizeof f); f[0] = 0; for (int i = 1; i <= n; i++) { while (l <= r && p[l] < pre[i]) s.erase(q[l]), l++; while (l <= r && b[p[r]] < b[i]) s.erase(q[r]), r--; p[++r] = i; q[r] = f[p[r - 1]] + b[i]; s.insert(q[r]); s.erase(q[l]); s.insert(q[l] = f[pre[i] - 1] + b[p[l]]); f[i] = *s.begin(); } printf("%d\n", f[n]); return 0; }
T3 [JZOJ4882] 多段线性函数
题目描述
数据范围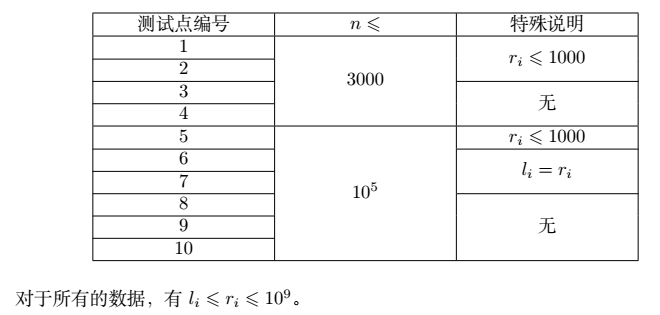
分析
通过人类智慧发现,$f_{min}(y)$ 是一个单峰函数,所以可以三分查找
但是,这题有一个优美的解法,就是把所有端点一起排序后取中间两个点为答案
同时,我有一个通俗易懂的证明
对于该答案区间,区间左右两侧的点数量一定相同
而题目中所给的所有区间,与答案区间一共有三种关系,分别是在答案区间左侧,在答案区间右侧,和包含答案区间
由于包含答案区间的区间的两端点一定分别在答案区间两侧,所以对两侧点数量关系没有影响
所以剩下的点一定是在答案区间左/右侧的区间的端点
这就很显然了,左右两侧的区间数量一定是相等的
对于一个动点,如果两侧区间数相等,那么它到所有区间的距离之和一定是不变的
当它向一侧不断移动时,与移动方向相同的一侧的区间数减少,反方向一侧的区间数增多,那么它到所有区间的距离之和是在不断变大的
所以,中间两点组成的区间一定是答案最优的区间

#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> using namespace std; #define ll long long #define inf 0x3f3f3f3f #define N 100005 int n; int p[2 * N]; int main() { freopen("linear.in", "r", stdin); freopen("linear.out", "w", stdout); scanf("%d", &n); for (int i = 1; i <= n; i++) scanf("%d%d", p + (i << 1) - 1, p + (i << 1)); sort(p + 1, p + (n << 1) + 1); printf("%d %d\n", p[n], p[n + 1]); return 0; }
T4 [JZOJ3430] DY引擎
题目描述
$BOSS$ 送给小唐一辆车。小唐开着这辆车从 $PKU$ 出发去 $ZJU$ 上课了。
众所周知,天朝公路的收费站超多的。经过观察地图,小唐发现从 $PKU$ 出发到 $ZJU$ 的所有路径只会有 $N$ 个不同的中转点,其中有 $M$ 个点是天朝的收费站。$N$ 个中转点标号为$1...N$,其中 $1$ 代表 $PKU$,$N$ 代表 $ZJU$。中转点之间总共有 $E$ 条双向边连接。
每个点还有一个附加属性,用 $0/1$ 标记,$0$ 代表普通中转点,$1$ 代表收费站。当然,天朝的地图上面是不会直接告诉你第 $i$ 个点是普通中转点还是收费站的。地图上有 $P$ 个提示,用 $[u, v, t]$ 表示:$[u, v]$ 区间的所有中转点中,至少有 $t$ 个收费站。数据保证由所有提示得到的每个点的属性是唯一的。
车既然是 $BOSS$ 送的,自然非比寻常了。车子使用了世界上最先进的 $DaxiaYayamao$ 引擎,简称 $DY$ 引擎。$DY$ 引擎可以让车子从 $U$ 瞬间转移到 $V$,只要 $U$ 和 $V$ 的距离不超过 $L$,并且 $U$ 和 $V$ 之间不能有收费站(小唐良民一枚,所以要是经过收费站就会停下来交完钱再走)。
$DY$ 引擎果然是好东西,但是可惜引擎最多只能用 $K$ 次。
小唐想知道从 $PZU$ 开到 $ZJU$ 用的最短距离(瞬间转移距离当然是按 $0$ 来计算的)。
数据范围
对于 $30\%$ 的数据,$2 \leq N \leq 30$,$max(0,N-10) \leq M \leq N$,$0 \leq K \leq 10$
对于 $100\%$ 的数据,$2 \leq N \leq 300$,$max(0,N-100) \leq M \leq N$,$E \leq 5 \times 10^4$,$1 \leq P \leq 3 \times 10^3$,$1 \leq L \leq 10^6$,$0 \leq K \leq 30$
分析
B组题难度果然有所提高啊 还有这个D(a)Y(a)??
这题一共分为两个部分,一个是找出所有收费站的位置连这种信息都不给我感到很遗憾,一个是找出最短路
首先题目给定了某两个站点间的收费站数量,这相当于一个差分约束系统
设 $s[i]$ 为从源点到 $i$ 之间的收费站数量,对于每个条件 $[u,v,t]$,有 $s[v]-s[u-1] \geq t$,即 $s[u-1]-s[v] \leq -t$
同时还有一些隐含条件 $s[i]-s[i-1] \geq 0$,即 $s[i-1]-s[i] \leq 0$;$s[i]-s[i-1] \leq 1$
对于每个形如 $v-u \leq w$ 的不等式,就连一条由 $u$ 指向 $v$ 权值为 $w$ 的有向边,然后在图上跑一边 $spfa$
最后得到的 $s[i]-s[i-1]$ 若等于 $1$ ,则说明 $i$ 位置上为收费站,否则为普通中转站
然后在原图上用 $floyd$ 处理出所有点之间不经过收费站的最短路,再把图分为 $K+1$ 层,在相邻两层图之间把最短路小于等于 $L$ 的两点用边权为 $0$ 的有向边连起来,最后用 $spfa$ 找出 $1$ 到 $n$ 的最短路即可

#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> using namespace std; #define ll long long #define inf 0x3f3f3f3f #define N 302 #define M 50002 #define K 32 int n, m, e, p, l, t, tot, ans = inf; int to[(M << 1) * K], len[(M << 1) * K], nxt[(M << 1) * K], head[N * K]; int edge[M][3], f[N][N], dis[N * K], vis[N * K]; void add(int u, int v, int w) { to[++tot] = v; len[tot] = w; nxt[tot] = head[u]; head[u] = tot; } void spfa(int x, int y) { memset(dis, 0x3f, sizeof dis); memset(vis, 0, sizeof vis); queue<int> q; dis[x] = y; q.push(x); while (!q.empty()) { int now = q.front(); q.pop(); vis[now] = 0; for (int i = head[now]; i; i = nxt[i]) if (dis[to[i]] > dis[now] + len[i]) { dis[to[i]] = dis[now] + len[i]; if (!vis[to[i]]) { vis[to[i]] = 1; q.push(to[i]); } } } } void floyd() { for (int k = 1; k <= n; k++) if (!(dis[k] - dis[k - 1])) for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) if (i != j && i != k && j != k) f[i][j] = min(f[i][j], f[i][k] + f[k][j]); } int main() { scanf("%d%d%d%d%d%d", &n, &m, &e, &p, &l, &t); memset(f, 0x3f, sizeof f); for (int i = 1; i <= e; i++) { int u, v, w; scanf("%d%d%d", &u, &v, &w); edge[i][0] = u; edge[i][1] = v; edge[i][2] = w; f[u][v] = f[v][u] = min(f[u][v], w); } for (int i = 1; i <= p; i++) { int u, v, w; scanf("%d%d%d", &u, &v, &w); add(v, u - 1, -w); } for (int i = 2; i <= n; i++) add(i, i - 1, 0), add(i - 1, i, 1); spfa(n, m); floyd(); memset(head, 0, sizeof head); tot = 0; for (int i = 1; i <= e; i++) for (int k = 0; k <= t; k++) { add(k * n + edge[i][0], k * n + edge[i][1], edge[i][2]); add(k * n + edge[i][1], k * n + edge[i][0], edge[i][2]); } for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) if (i != j && f[i][j] <= l) for (int k = 0; k < t; k++) add(k * n + i, (k + 1) * n + j, 0); spfa(1, 0); for (int k = 0; k <= t; k++) ans = min(ans, dis[k * n + n]); printf("%d\n", ans); return 0; }




