2019-08-05 纪中NOIP模拟B组
T1 [JZOJ1432] 输油管道
题目描述
请你帮忙设计一个从城市 $M$ 到城市 $Z$ 的输油管道,现在已经把整个区域划分为 $R$ 行 $C$ 列,每个单元格可能是空的也可能是以下 $7$ 种基本管道之一:
油从城市 $M$ 流向 $Z$,'$+$' 型管道比较特殊,因为石油必须在两个方向(垂直和水平)上传输,如下图所示:
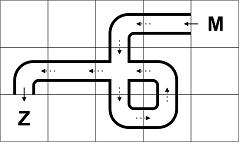
现在恐怖分子弄到了输油管道的设计图,并把其中一个单元格中的管道偷走了,请你帮忙找到偷走的管道的位置以及形状。
数据保证石油的流向是唯一的,只有一个管道跟 $M$ 和 $Z$ 相连,除此此外,保证没有多余的管道,也就是说所有的管道在加进被偷的管道后一定都会被用上。
数据保证有解而且是唯一的。
数据范围
$1 \leq R,C \leq 25$
分析
开局打150行搜索的我就是个铁憨憨,这题浪费了好多时间啊...
由于起点和终点之间的管道是唯一的,所以只要枚举每个单元格中的管道,如果管道通向了空地,那么这片空地就是被拆除管道的位置
然后通过判断该位置需要连接的方向,就可以得到管道形状
如果是起点或终点旁边的管道被拆除,就需要进行一些特判

#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> using namespace std; #define ll long long #define inf 0x3f3f3f3f #define N 30 int n, m, x, y, x1, y1, x2, y2, s, e; int book[4], d[4][2] = {0, 1, 1, 0, 0, -1, -1, 0}; char g[N][N]; void check(int i, int j, int dir) { int dx = i + d[dir][0], dy = j + d[dir][1]; if (g[dx][dy] == '.') x = dx, y = dy, book[(dir + 2) % 4] = 1; else if (g[dx][dy] == 'M') s = 1; else if (g[dx][dy] == 'Z') e = 1; } int main() { scanf("%d%d", &n, &m); for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) { scanf(" %c", &g[i][j]); if (g[i][j] == 'M') x1 = i, y1 = j; if (g[i][j] == 'Z') x2 = i, y2 = j; } for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) { if (g[i][j] == '|') check(i, j, 1), check(i, j, 3); else if (g[i][j] == '-') check(i, j, 0), check(i, j, 2); else if (g[i][j] == '+') check(i, j, 0), check(i, j, 1), check(i, j, 2), check(i, j, 3); else if (g[i][j] == '1') check(i, j, 0), check(i, j, 1); else if (g[i][j] == '2') check(i, j, 0), check(i, j, 3); else if (g[i][j] == '3') check(i, j, 2), check(i, j, 3); else if (g[i][j] == '4') check(i, j, 1), check(i, j, 2); } if (!s && !e) { if (x1 == x2) printf("%d %d -", x1, (y1 + y2) >> 1); else printf("%d %d |", (x1 + x2) >> 1, y1); } else { if (!s) { for (int i = 0; i < 4; i++) if (x1 + d[i][0] == x && y1 + d[i][1] == y) book[(i + 2) % 4] = 1; } else if (!e) { for (int i = 0; i < 4; i++) if (x2 + d[i][0] == x && y2 + d[i][1] == y) book[(i + 2) % 4] = 1; } if (book[0] && book[1] && book[2] && book[3]) printf("%d %d +", x, y); else if (book[1] && book[3]) printf("%d %d |", x, y); else if (book[0] && book[2]) printf("%d %d -", x, y); else if (book[0] && book[1]) printf("%d %d 1", x, y); else if (book[0] && book[3]) printf("%d %d 2", x, y); else if (book[2] && book[3]) printf("%d %d 3", x, y); else if (book[1] && book[2]) printf("%d %d 4", x, y); } return 0; }
T2 [JZOJ1433] 数码问题
题目描述
$Alice$ 有一个 $N \times N$ 的格子,把 $1 \sim N^2$ 按照从上到下从左到右的顺序填进表格中,允许在表格上进行两种操作:
(1) 旋转行——这一行的数向右移动一个位置,而最后一列的数会移到第一列;
(2) 旋转列——这一列的数向下移动一个位置,最后一行的数会移到第一行。
$Alice$ 想把数 $X$ 移到 $(R,C)$ 处可以采用以下方法:
• 如果 $X$ 不在 $C$ 这一列,通过旋转行操作把 $X$ 移到 $C$ 这一列;
• 如果 $X$ 不在 $R$ 这一行,通过旋转列操作把 $X$ 移到 $R$ 这一行。
$Alice$ 现在想采用上述方法,依次把 $K$ 个数移到各自的目标位置,编程计算每个数需要几次操作。
数据范围
$1 \leq N \leq 10^4$,$1 \leq K \leq 10^3$
分析
如果每次都将整个矩阵移动,那么 $O(nk)$ 不仅会 $TLE$ 的,还会 $MLE$
实际上真正需要用到的数字只有 $K$ 个,其他数字在题中其实是无效的
所以只需要记录这 $K$ 个数字的位置,每次把他们移动就可以了

#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> using namespace std; #define ll long long #define inf 0x3f3f3f3f #define N 1005 int n, m, k, l1, l2, ans; int x[N], y[N], r[N], c[N]; int main() { scanf("%d%d", &n, &k); for (int i = 1; i <= k; i++) { scanf("%d%d%d", &m, r + i, c + i); x[i] = (m + n - 1) / n; y[i] = m - (x[i] - 1) * n; } for (int i = 1; i <= k; i++) { l1 = (c[i] - y[i] + n) % n; for (int j = 1; j <= k; j++) if (x[i] == x[j]) { y[j] += l1; if (y[j] > n) y[j] -= n; } l2 = (r[i] - x[i] + n) % n; for (int j = 1; j <= k; j++) if (y[i] == y[j]) { x[j] += l2; if (x[j] > n) x[j] -= n; } printf("%d\n", l1 + l2); } return 0; }
T3 [JZOJ1434] 灌水
题目描述
学生都很喜欢灌水,第一天只有 $Alice$ 给她的每个朋友灌了一次水,从第二天开始,所有学生(包括 $Alice$)将会有规律地去灌水:
• 如果前一天被灌了奇数次的水,他们将会给每个朋友灌一次水;
• 如果前一天被灌了偶数次的水,他们将会给每个朋友灌两次水。
学生编号为 $1$ 到 $N$,$Alice$ 为 $1$ 号,学生之间的朋友关系会给出。
计算 $H$ 天后一共灌了几次水。
数据范围
对于 $50 \%$ 的数据,$1 \leq H \leq 10^3$
对于 $100 \%$ 的数据,$1 \leq N \leq 20$,$1 \leq H \leq 10^9$
分析
看这个数据范围,显然状压,$0$ 表示前一天被灌了偶数次水,$1$ 表示前一天被灌了奇数次水
然后如果是一天天推过去,只能得到 $50 \, pts$
但其实状压的所有状态只有 $2^n$ 种,所以在 $2^n$ 天内一定会出现至少一次循环
所以只需要找出这个循环节,就不用把每一天的状态都推出来了
时间复杂度就优化为了 $O(2^n n)$

#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> using namespace std; #define ll long long #define inf 0x3f3f3f3f #define N 21 ll ans, pre[1 << N]; int n, h, k, t, last, now; int g[N], book[1 << N], cnt[N]; char c[25]; int main() { scanf("%d%d", &n, &h); for (int i = 1; i <= n; i++) { scanf("%s", c + 1); for (int j = n; j >= 1; j--) { if (c[j] == '0') g[i] <<= 1; else g[i] = (g[i] << 1) | 1, cnt[i]++; } } ans += cnt[1]; now = g[1]; pre[1] = ans; book[now] = 1; for (k = 2; k <= h; k++) { last = now; now = 0; for (int i = 1; i <= n; i++) { if (last & (1 << i - 1)) { ans += cnt[i]; now ^= g[i]; } else ans += cnt[i] * 2; } pre[k] = ans; if (book[now]) break; book[now] = k; } if (k >= h) {printf("%lld\n", ans); return 0;} t = (h - book[now]) / (k - book[now]); ans += (t - 1) * (pre[k] - pre[book[now]]); k += (t - 1) * (k - book[now]) + 1; for (; k <= h; k++) { last = now; now = 0; for (int i = 1; i <= n; i++) { if (last & (1 << i - 1)) { ans += cnt[i]; now ^= g[i]; } else ans += cnt[i] * 2; } } printf("%lld\n", ans); return 0; }
T4 [JZOJ1435] 开花
题目描述
在遥远的火星上,上面的植物非常奇怪,都是长方形的,每个植物用三个数来描述:左边界 $L$、右边界 $R$ 以及高度 $H$,如下图所示描述一个植物:$L=2$,$R=5$ 和 $H=4$。
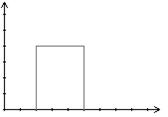
每天都有一个新植物长出来,第一天的植物高度为 $1$,后面每天长出的植物比前一天的高 $1$。
当一个新植物长出来的时候,跟其他植物的水平线段相交处会长出一朵小花(前提是之前没有长出花朵),如果线段交于端点,是不会长花的。
下面为示意图:
给出每天的植物的坐标,计算每天长出多少新花。
数据范围
$1 \leq N \leq 10^5$,$1 \leq L \leq R \leq 10^5$
分析
线段树区间修改+单点查询

#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> using namespace std; #define ll long long #define inf 0x3f3f3f3f #define N 100005 #define lc (p << 1) #define rc ((p << 1) | 1) #define mid ((l + r) >> 1) int n, m; int L[N], R[N], sum[N]; struct Tree { int val, mark; } t[4 * N]; void build(int p, int l, int r) { t[p].val = t[p].mark = 0; if (l == r) return; build(lc, l, mid); build(rc, mid + 1, r); } void pushDown(int p, int l, int r) { if (t[p].mark) { t[lc].val += t[p].mark * (mid - l + 1); t[rc].val += t[p].mark * (r - mid); t[lc].mark += t[p].mark; t[rc].mark += t[p].mark; t[p].mark = 0; } } void update(int p, int l, int r, int ql, int qr) { if (l > qr || r < ql) return; if (l >= ql && r <= qr) { t[p].val += (r - l + 1); t[p].mark += 1; return; } pushDown(p, l, r); update(lc, l, mid, ql, qr); update(rc, mid + 1, r, ql, qr); t[p].val = t[lc].val + t[rc].val; } int query(int p, int l, int r, int q) { if (l > q || r < q) return 0; if (l == r) return t[p].val; pushDown(p, l, r); return query(lc, l, mid, q) + query(rc, mid + 1, r, q); } int main() { scanf("%d", &n); for (int i = 1; i <= n; i++) { scanf("%d%d", L + i, R + i); m = max(m, R[i]); } build(1, 1, m); for (int i = 1; i <= n; i++) { int v1, v2; if (R[i] - L[i] > 1) update(1, 1, m, L[i] + 1, R[i] - 1); v1 = query(1, 1, m, L[i]); v2 = query(1, 1, m, R[i]); printf("%d\n", v1 - sum[L[i]] + v2 - sum[R[i]]); sum[L[i]] = v1; sum[R[i]] = v2; } return 0; }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号