并查集
板子
int find(int x);
void uniona(int x, int y);
------------------------------------------------------------
int p[N]; //p是父亲数组
for(int i = 1; i <= n; i++) p[i] = i; //初始化
int p1 = find(a), p2 = find(b); //单独写出来,避免多次调用函数;p1是a的根节点,p2是b的根节点
if(p1 == p2); //在一个集合中
else uniona(p1, p2); //不在一个集合中
int find(int x) //寻找根节点 + 路径压缩
{
int a = x; //保存x的值,为下面路径压缩做准备
while(a != p[a]) a = p[a]; //递推寻找根节点
int b = x;
while(b != a) //写p[b] != a也可以,因为是根节点的时候,p[b] = b
{
int c = p[b];
p[b] = a;
b = c; //为下一次循环将b原来的父亲的父亲设为根节点做准备
}
return a;
}
void uniona(int x, int y)
{
p[find(x)] = find(y);
}
p[x] = y ; //x的父亲是y
路径压缩
将每个点的父亲都设为根节点,这样会更加方便
用递推 ——> 递归可能会导致溢出栈
>1【模板】并查集
题目描述
如题,现在有一个并查集,你需要完成合并和查询操作。
输入格式
第一行包含两个整数 \(N,M\) ,表示共有 \(N\) 个元素和 \(M\) 个操作。
接下来 \(M\) 行,每行包含三个整数 \(Z_i,X_i,Y_i\) 。
当 \(Z_i=1\) 时,将 \(X_i\) 与 \(Y_i\) 所在的集合合并。
当 \(Z_i=2\) 时,输出 \(X_i\) 与 \(Y_i\) 是否在同一集合内,是的输出
Y ;否则输出 N 。
输出格式
对于每一个 \(Z_i=2\) 的操作,都有一行输出,每行包含一个大写字母,为 Y 或者 N 。
样例
4 7
2 1 2
1 1 2
2 1 2
1 3 4
2 1 4
1 2 3
2 1 4
N
Y
N
Y
提示
对于 \(100\%\) 的数据,\(1\le N \le 10^4\),\(1\le M \le 2\times 10^5\),\(1 \le X_i, Y_i \le N\),\(Z_i \in \{ 1, 2 \}\)。
代码
#include <iostream>
using namespace std;
const int N = 1e4 + 10;
int p[N];
int find(int x);
void uniona(int x, int y);
int main()
{
int n, m; cin >> n >> m;
for(int i = 1; i <= n; i++) p[i] = i;
while(m--)
{
int z, x, y; cin >> z >> x >> y;
int p1 = find(x), p2 = find(y);
if(z == 1) uniona(p1, p2);
else
{
if(p1 == p2) cout << "Y" << endl;
else cout << "N" << endl;
}
}
}
int find(int x)
{
int a = x;
while(a != p[a]) a = p[a];
int b = x;
while(b != a)
{
int c = p[b];
p[b] = a;
b = c;
}
return a;
}
void uniona(int x, int y)
{
p[x] = y;
}
>2 亲戚
题目背景
若某个家族人员过于庞大,要判断两个是否是亲戚,确实还很不容易,现在给出某个亲戚关系图,求任意给出的两个人是否具有亲戚关系。
题目描述
规定:\(x\) 和 \(y\) 是亲戚,\(y\) 和 \(z\) 是亲戚,那么 \(x\) 和 \(z\) 也是亲戚。如果 \(x\),\(y\) 是亲戚,那么 \(x\) 的亲戚都是 \(y\) 的亲戚,\(y\) 的亲戚也都是 \(x\) 的亲戚。
输入格式
第一行:三个整数 \(n,m,p\),(\(n,m,p \le 5000\)),分别表示有 \(n\) 个人,\(m\) 个亲戚关系,询问 \(p\) 对亲戚关系。
以下 \(m\) 行:每行两个数 \(M_i\),\(M_j\),\(1 \le M_i,~M_j\le n\),表示 \(M_i\) 和 \(M_j\) 具有亲戚关系。
接下来 \(p\) 行:每行两个数 \(P_i,P_j\),询问 \(P_i\) 和 \(P_j\) 是否具有亲戚关系。
输出格式
\(p\) 行,每行一个 Yes 或 No。表示第 \(i\) 个询问的答案为“具有”或“不具有”亲戚关系。
样例
6 5 3
1 2
1 5
3 4
5 2
1 3
1 4
2 3
5 6
Yes
Yes
No
代码
#include <iostream>
using namespace std;
const int N = 5010;
int p[N];
int find(int x);
void uniona(int x, int y);
int main()
{
int n, m, q; cin >> n >> m >> q;
for(int i = 1; i <= n; i++) p[i] = i;
while(m--)
{
int x, y; cin >> x >> y;
uniona(find(x), find(y));
}
while(q--)
{
int x, y; cin >> x >> y;
if(find(x) == find(y)) cout << "Yes" << endl;
else cout << "No" << endl;
}
}
int find(int x)
{
int a = x;
while(a != p[a]) a = p[a];
int b = x;
while(b != a)
{
int c = p[b];
p[b] = a;
b = c;
}
return a;
}
void uniona(int x, int y)
{
p[x] = y;
}
>3 朋友
题目背景
小明在 A 公司工作,小红在 B 公司工作。
题目描述
这两个公司的员工有一个特点:一个公司的员工都是同性。
A 公司有 \(N\) 名员工,其中有 \(P\) 对朋友关系。B 公司有 \(M\) 名员工,其中有 \(Q\) 对朋友关系。朋友的朋友一定还是朋友。
每对朋友关系用两个整数 \((X_i,Y_i)\) 组成,表示朋友的编号分别为 \(X_i,Y_i\)。男人的编号是正数,女人的编号是负数。小明的编号是 \(1\),小红的编号是 \(-1\)。
大家都知道,小明和小红是朋友,那么,请你写一个程序求出两公司之间,通过小明和小红认识的人最多一共能配成多少对情侣(包括他们自己)。
输入格式
输入的第一行,包含 \(4\) 个空格隔开的正整数 \(N,M,P,Q\)。
之后 \(P\) 行,每行两个正整数 \(X_i,Y_i\)。
之后 \(Q\) 行,每行两个负整数 \(X_i,Y_i\)。
输出格式
输出一行一个正整数,表示通过小明和小红认识的人最多一共能配成多少对情侣(包括他们自己)。
样例
4 3 4 2
1 1
1 2
2 3
1 3
-1 -2
-3 -3
2
提示
对于 \(100 \%\) 的数据,\(N,M \le 10^4\),\(P,Q \le 2 \times 10^4\)。
代码
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e4 + 10;
int pa[N], pb[N], cnta[N], cntb[N]; //分开统计男女朋友数,最小值就是所求
int finda(int x);
int findb(int x);
int main()
{
int n, m, k, h; cin >> n >> m >> k >> h;
for(int i = 1; i <= n; i++) pa[i] = i, cnta[i] = 1;
for(int i = 1; i <= m; i++) pb[i] = i, cntb[i] = 1; //将负值变为正值更方便
while(k--)
{
int x, y; cin >> x >> y;
int p1 = finda(x), p2 = finda(y);
if(p1 != p2) //将1作为男生总的根节点
{
if(p1 == 1) pa[p2] = p1, cnta[p1] += cnta[p2];
else if(p2 == 1) pa[p1] = p2, cnta[p2] += cnta[p1];
else pa[p1] = p2, cnta[p2] += cnta[p1];
}
}
while(h--)
{
int x, y; cin >> x >> y;
x = -x, y = -y;
int p1 = findb(x), p2 = findb(y);
if(p1 != p2) //将-1作为女生总的根节点,负变正之后就是将1作为总的根节点
{
if(p1 == 1) pb[p2] = p1, cntb[p1] += cntb[p2];
else if(p2 == 1) pb[p1] = p2, cntb[p2] += cntb[p1];
else pb[p1] = p2, cntb[p2] += cntb[p1];
}
}
int num = min(cnta[1], cntb[1]);
cout << num;
}
int finda(int x)
{
int a = x;
while(a != pa[a]) a = pa[a];
int b = x;
while(b != a)
{
int c = pa[b];
pa[b] = a;
b = c;
}
return a;
}
int findb(int x)
{
int a = x;
while(a != pb[a]) a = pb[a];
int b = x;
while(b != a)
{
int c = pb[b];
pb[b] = a;
b = c;
}
return a;
}
>4 银河英雄传说
简化版题目
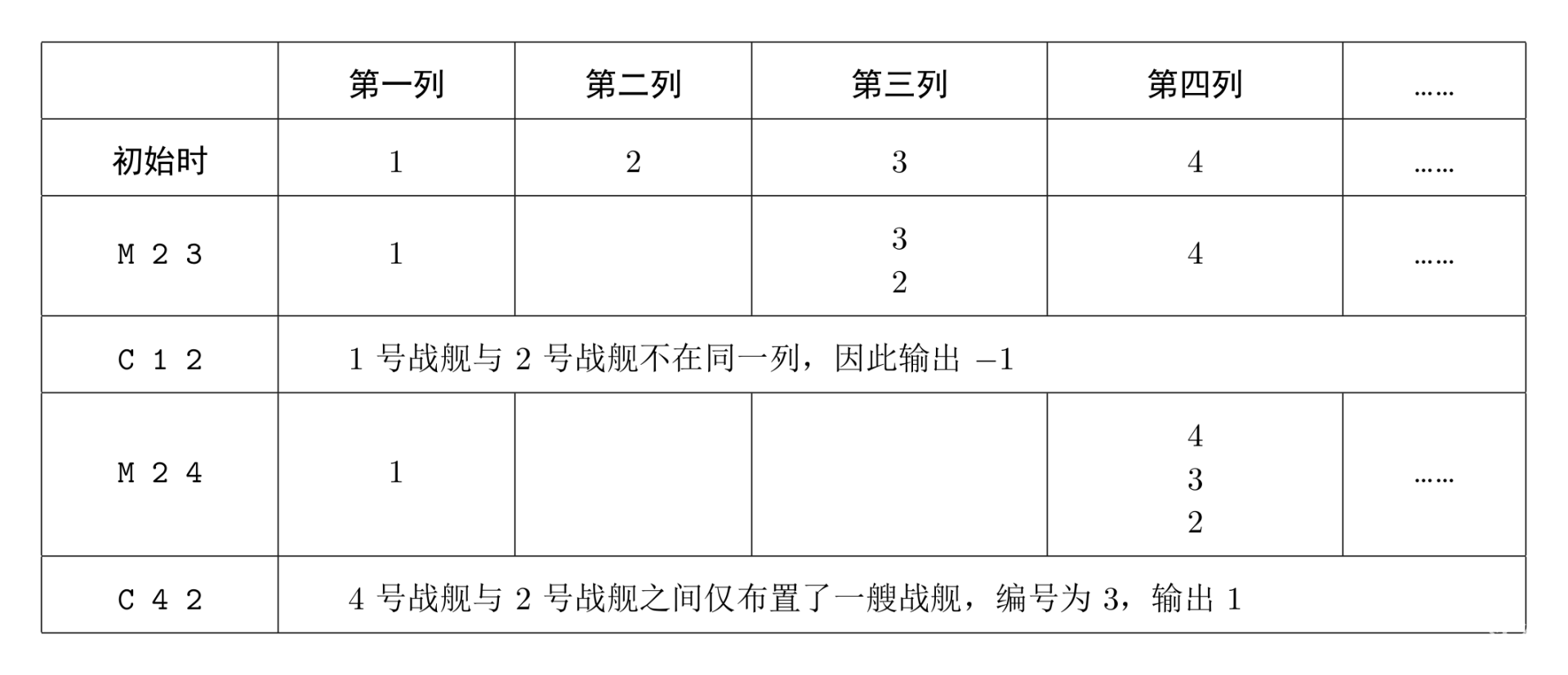
A将战舰划分成\(30000\)列,每列依次编号为\(1, 2,...,30000\)。战舰也依次编号为 \(1, 2, ..., 30000\),让第\(i\) 号战舰处于第$ i$ 列。
合并指令为\(M\) \(i\) \(j\),第\(i\)号战舰整体(头在前尾在后)接至第 \(j\)号战舰所在队列的尾部。战舰队列是由处于同一列的战舰组成的。
\(B\)在\(A\)发布指令调动舰队的同时,也会发出一些询问指令:\(C\) \(i\) \(j\)。\(A\)的第\(i\)号战舰与第\(j\)号战舰当前是否在同一列中,如果在同一列中,那么它们之间布置有多少战舰。
输入格式
第一行有一个整数 \(T\)(\(1 \le T \le 5 \times 10^5\)),表示总共有 \(T\) 条指令。
以下有 \(T\) 行,每行有一条指令。指令有两种格式:
-
M i j:\(i\) 和 \(j\) 是两个整数(\(1 \le i,j \le 30000\)),表示指令涉及的战舰编号。该指令是莱因哈特窃听到的杨威利发布的舰队调动指令,并且保证第 \(i\) 号战舰与第 \(j\) 号战舰不在同一列。 -
C i j:\(i\) 和 \(j\) 是两个整数(\(1 \le i,j \le 30000\)),表示指令涉及的战舰编号。该指令是莱因哈特发布的询问指令。
输出格式
- 调动指令不要输出任何信息。
- 询问指令:在同一列上,输出第 \(i\) 号战舰与第 \(j\) 号战舰之间布置的战舰数目。不在同一列上,则输出 \(-1\)。
样例
4
M 2 3
C 1 2
M 2 4
C 4 2
-1
1
提示
样例解释
战舰位置图:表格中阿拉伯数字表示战舰编号。
题目中没有强制 \(i \neq j\),但是实测数据中不存在 \(i = j\) 的情况。
代码
#include <iostream>
using namespace std;
const int N = 3e4 + 10;
int p[N], cnt[N], d[N]; //cnt记录每一列的数量, d记录该点到根节点的距离
int find(int x);
void uniona(int p1, int p2);
int main()
{
int t; cin >> t;
for(int i = 1; i <= 30000; i++) p[i] = i, cnt[i] = 1;
while(t--)
{
char c;
int a, b; cin >> c >> a >> b;
int p1 = find(a), p2 = find(b);
if(c == 'M') uniona(p1, p2);
else
{
if(p1 != p2) cout << -1 << endl;
else cout << abs(d[a] - d[b]) - 1 << endl; //初始d[i]为0,所以计算中间个数的时候要减1
}
}
}
int find(int x)
{
if(p[x] == x) return x;
int p1 = p[x], p2 = find(p[x]);
p[x] = p2;
d[x] += d[p1];
return p2;
}
void uniona(int p1, int p2)
{
p[p1] = p2;
d[p1] = cnt[p2];
cnt[p2] += cnt[p1];
cnt[p1] = 0;
}





