cf round 898 (div.4) E

建造水族馆

题目描述

你喜欢鱼，所以你决定建造一个水族馆。你有一块由 n 根柱子组成的珊瑚，其中 i 根柱子高 ai 个单位。之后，你将在珊瑚周围建造一个水族箱，具体如下：

• 选择一个整数 h --水箱的高度。在水箱两侧建造高度为 h 的墙壁。
• 然后，在水箱中注满水，使每一列的高度都是 h ，珊瑚的高度超过 h 这一列就不能注水。

例如， a=[3,1,2,4,6,2,5] ，高度为 h=4 ，最终总共需要使用 w=8 个单位的水，如图所示。

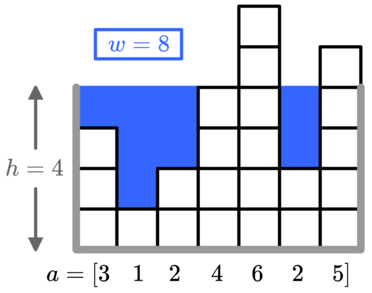
你最多可以用 x 个单位的水来装满水箱，但你想尽可能建造最大的水箱。你能选择的 h 的最大值 是多少？

输入

第一行包含一个整数 t( 1 <= t <= 10 ⁴ ) - 测试用例数。

每个测试用例的第一行包含两个正整数 n 和 x( 1 <= n <= 2 * 10⁵ ; 1 <= x <= 10⁹ )--珊瑚的列数和最大水量。

每个测试用例的第二行包含 n 个空格分隔的整数 ai ( 1 <= a1 <= 10⁹; 1 <= x <= 10⁹ )。( 1 <= ai <= 10⁹) - 珊瑚的高度。

所有测试用例中 n 的总和不超过 2 * 10⁵ 。

输出

对于每个测试用例，输出一个正整数 h ( h >= 1 ) - 水箱的最大高度，因此最多需要 x 个单位的水才能装满水箱。

我们已经证明，在这些限制条件下， h 这个值总是存在的。

测试样例

输入

5
7 9
3 1 2 4 6 2 5
3 10
1 1 1
4 1
1 4 3 4
6 1984
2 6 5 9 1 8
1 1000000000
1

输出

4
4
2
335
1000000001

样例解释

第一个测试案例如语句所示。在 h=4 的情况下，我们需要 8 单位的水，但如果将 h 增加到 5 ，我们需要13 单位的水，这比 x=9 多。所以 h=4 是最佳方案。

在第二个测试案例中，我们可以选择 h=4 ，并在每列中添加 3 个单位，总共使用 9 个单位的水。可以证明这是最佳方案。

在第三个测试案例中，我们可以选择 h=2 ，并使用所有的水，因此这是最优方案。

易错

上边界是珊瑚最大高度和最大水量高度的总和，并非只是最大水量的高度，所以r初始化为2e9 + 10，而不是1e9 + 10

• 样例5 则说明了这一点，只有一个珊瑚，结果就是最大水量和珊瑚高度加在一起

代码

#include <iostream>

const int N = 2e5 + 10;
long long a[N];
using namespace std;

int main()
{
    int t; cin >> t;
    while(t--)
    {
        int n, x;
        long long max = 0;
        cin >> n >> x;
        for(int i = 0; i < n; i++) cin >> a[i];
        long long l = 0, r = 2e9 + 10;
        while(l < r)
        {
            long long mid = l + r + 1 >> 1;
            long long ans = 0;
            bool goal = true;
            for(int i = 0; i < n; i++)
            {
                if(a[i] < mid) ans += mid - a[i];
                if(x < ans)
                {
                    r = mid - 1, goal = false;    //若不满足条件，则说明h过高，要降低h；所以要在左边寻找，当前的mid不满足条件
                    break;
                }
            }
            if(goal) l = mid;
        }
        cout << l << endl;
    }
}