浅谈FFT、NTT和MTT
前言
\(\text{FFT}\)(快速傅里叶变换)是 \(O(n\log n)\) 解决多项式乘法的一个算法,\(\text{NTT}\)(快速数论变换)则是在模域下的,而 \(\text{MTT}\)(毛神仙对\(\text{FFT}\)的精度优化算法)可以针对任意模数。
正文
FFT-快速傅里叶变换
学习这个算法可以借助《算法导论》,当然算导上的东西需要耐心才能啃下来。这里只是概括一下算导上的介绍,并加入一些个人的见解。下面逐步介绍这个算法。
复数
如果学过的话可以跳过。实数可以一一对应数轴上的点,那么复数就可以一一对应平面直角坐标系上的点。对应 \(x\) 轴上的点的就是我们熟悉的实数,而外面的就是虚数。其中 \((0,1)\) 这个点对应的数记作 \(i\) ,即 \(\sqrt{-1}\),它表示虚数单位。复数可以表示成 \(a+ib\) 的形式,其中 \(a,b\) 为实数。
极坐标表示法下的乘法
证明如下:
代数表示法下的乘法
无需证明,肉眼化简。
单位复数根
在单位圆上,我们用 \(\omega_{n}^k\) 表示将单位圆 \(n\) 等分,取其第 \(k\) 条线对应的单位复数。其中 \(\omega_n^0=1\) ,逆时针方向编号,如图所示:
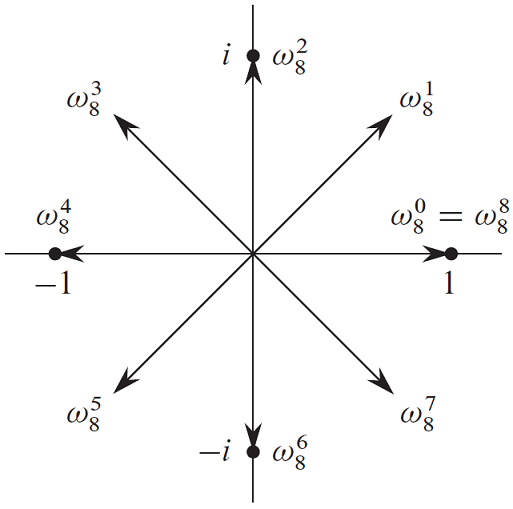
单位复根有一些重要的性质。
消去引理
折半引理
如果借助向量去理解的话,理解起来非常方便。
多项式
一个形如 \(\displaystyle A(x)=\sum_{i=0}^{n-1}a_ix^i\) 的式子。
系数表示
直接列出 \(A(x)\) 的各项系数。这种表示方法可以 \(O(n)\) 的实现多项式加法,但多项式乘法却需要 \(O(n^2)\)
点值表示
通过带入若干个特值确定,显然,一个最高次为 \(n-1\) 的多项式需要 \(n\) 的特殊值便唯一确定。这种表示方法可以 \(O(n)\) 的加和乘,但是要转化成系数表示才能体现出它作为多项式的价值。
DFT
对于一个列向量 \(a=(a_0,a_1,\cdots,a_{n-1})\) ,以它为系数的多项式 \(A(x)=\displaystyle\sum_{j=0}^{n-1}a_jx^j\)
若有一个列向量 \(y=(y_0,y_1,\cdots,y_{n-1})\) 满足 \(y_k=A(\omega_n^k)\) ,则\(y=\text{DFT}_n(a)\)
\(\text{DFT}\) 的全称为离散傅里叶变换,是将多项式的系数表达化作点值表达的一个变换。
同理 \(a=\text{DFT}_n^{-1}(y)\) ,\(\text{DFT}^{-1}\) 就是逆离散傅里叶变换,也称 \(\text{IDFT}\),我们尝试写出 \(\text{DFT}^{-1}\) 的表达式。
写出 \(y\) 与 \(a\) 的关系
然后我们可以矩阵乘积 \(y=V_na\) 的形式表示向量 \(a\) 到向量 \(y\) 的变换。\(V_n\) 为由 \(\omega_n\) 各项指数构成的范德蒙德矩阵。
那我们现在要求的就是 \(V_n^{-1}\) 的矩阵,即 \(V_n\) 的逆矩阵。
有如下定理:
对于 \(j,k\in[0,n)\) ,有 \([V_n^{-1}]_{jk}=\omega_n^{-j,k}/n\)
证明如下
显然,当 \(j=j'\) 时,\([V_nV_n^{-1}]_{jj'}\) 的值为 \(1\) ,否则为 \(0\) ,那么 \([V_nV_n^{-1}]\) 是一个行列数为 \(n\) 的单位矩阵,即得证 \(V^{-1}\) 为 \(V\) 的逆矩阵。
那么在作 \(\text{IDFT}\) 的时候,只需将单位根换成 \({\omega_n^{-1}}\) ,最后系数再除以 \(n\) 即可。
当然,直接变换是 \(O(n^2)\) 的。我们考虑用分治的思想进行变换。
FFT
首先观察多项式 \(A(x)\) ,我们将指数分奇偶两类。偶数项以 \(\{a_0,a_2,...,a_{n-2}\}\) 构造一个新的多项式 \(\displaystyle A^{[0]}(x)=\sum_{j=0}^{n/2-1}a_{2j}x^j\),奇数项同理为 \(\displaystyle A^{[1]}(x)=\sum_{j=0}^{n/2-1}a_{2j+1}x^j\)。
那么显然有
我们把 \(\omega_n^k\) 代入得到
利用消去引理得到
那么将 \(A^{[0]},A^{[1]}\) 的系数向量 \(a^{[0]},a^{[1]}\) 进行一次 \(\text{DFT}\) ,分别得到 \(y^{[0]},y^{[1]}\) 。
有
只要令 \(k<n/2\) ,将 \(k\geq n/2\) 的部分用折半引理即可。
推导不难,注意将在单位圆上的旋转借用平面向量来理解。
用 \(y\) 代入,最终的表达式为
这样就可以分治求解了。
更高效的FFT
事实上 \(\text{FFT}\) 可以迭代求解。先观察一下递归求解的过程,如图所示。
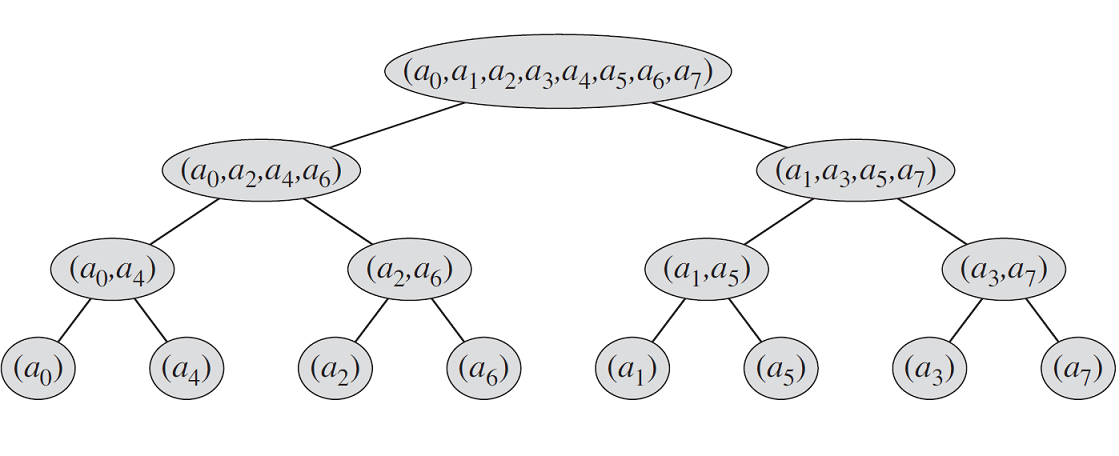
用人类智慧观察,发现 \(a_i\) 在底层是在的位置为 \(i\) 的二进制位翻转。
发现只需要枚举区间长度,扫整个序列,就可以进行对区间进行合并。观察递归求解的式子
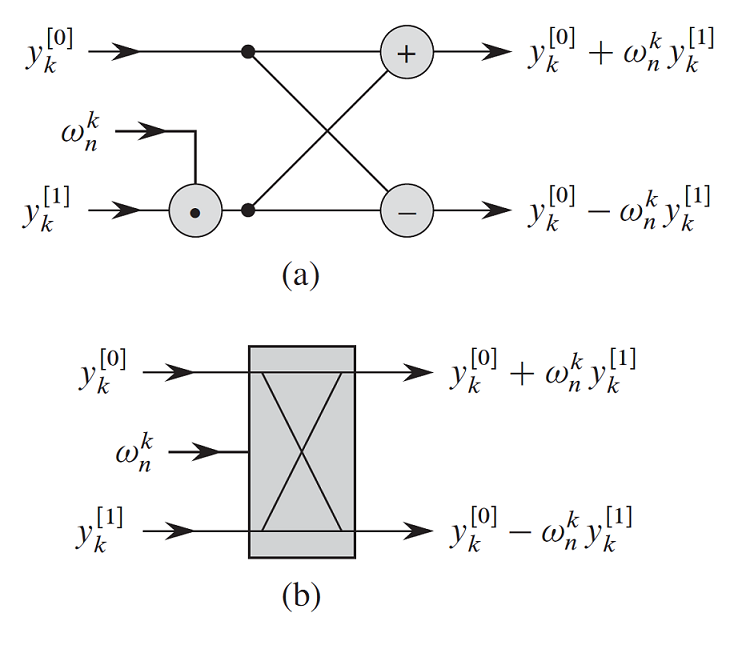
它的流程可以用上图来表示,上面操作叫作蝴蝶操作,其实和递归求解的流程相似。具体还是看代码。
void DFT(Complex *a, int op, int n)
{
static int rev[N], pre = 0;
static Complex w[N];
if(pre != n)
{
rev[0] = 0;
FOR(i, 1, n - 1) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) * (n >> 1));
FOR(i, 0, n - 1) w[i] = (Complex){cos(2 * pi * i / n), sin(2 * pi * i / n)};
pre = n;
}
FOR(i, 0, n - 1) if(i < rev[i]) std::swap(a[i], a[rev[i]]);
for(int i = 2; i <= n; i <<= 1)
for(int j = 0; j < n; j += i)
for(int k = 0; k < i / 2; ++k)
{
Complex u = a[j + k];
Complex t = w[op == 1 ? n / i * k : (n - 1) & (n - n / i * k)] * a[j + k + i / 2];
a[j + k] = u + t;
a[j + k + i / 2] = u - t;
}
if(op == -1)
{
FOR(i, 0, n - 1) a[i] = a[i] / n;
}
}
显而易见,由于 \(\text{double}\) 的存在,精度多多少少会被卡一点。而具体的题目经常往往会给一个特殊的模数,这种时候就要用到接下来介绍的算法了。

