BZOJ 3172 单词（AC自动机）

题意

https://www.lydsy.com/JudgeOnline/problem.php?id=3172

思路

\(\text{AC}\)自动机模板题，稍微点一下 \(\text{AC}\)自动机。

\(\text{AC}\)自动机说白了就是在 \(\text{Trie}\) 树上跑 \(\text{KMP}\)。

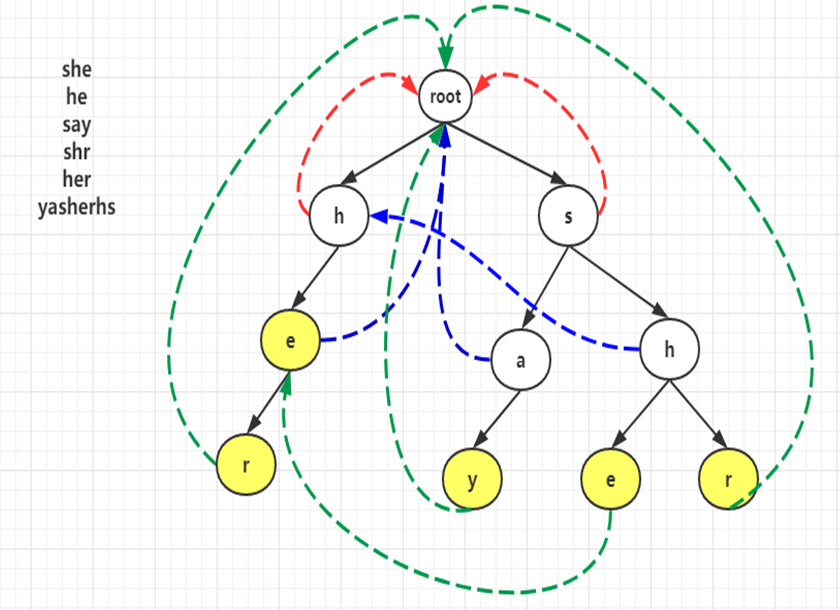
它通过广搜来预处理 \(fail\) 指针。一个从节点 \(a\) 到节点 \(b\) 的 \(fail\) 指针，代表除 \(a\) 本身外，最长能在自动机上找到的后缀 。如上图从字母e指向字母e的指针。同时处理出在自动机上的每一个节点，之后再向自动机内输入哪个字母，它会跑到哪里（省去了跳 \(fail\) 指针的过程），直接用 \(Trie\) 树的 \(ch\) 数组表示（将 \(Trie\) 树变成了 \(Trie\) 图），在 \(\text{KMP}\) 的部分题目中已经体现出了这种思想。

其实整个算法中最重要的还是 \(fail\) 指针，\(fail\) 指针代表后缀相等。不难发现，\(fail\) 指针构成了一棵树，每跳一次 \(fail\) 指针，在 \(Trie\) 树上的深度至少减 \(1\) 。\(fail\) 的树形结构在解题中尤为关键。

还有关于“自动机”一词，我想可以这样理解，先将模式串构成自动机，文本串一个字符一个字符的输入这个机器，\(ch\) 数组表示匹配指针的跳动，并用 \(fail\) 指针将影响传递给所有需要影响的位置。

这题是\(\text{AC}\)自动机最基础的运用之一。首先将模式串（即文章中的单词）建立自动机，然后将文章输入自动机。由于要传递影响，暴力的写法是所有匹配指针到的位置都应该跳 \(fail\) 指针直到根，中途节点答案加一，但是这样复杂度过不去。利用 \(fail\) 的树形结构，直接在匹配指针到的位置加 \(1\) ，最后一遍差分上来即可。

代码

#include<bits/stdc++.h>
#define FOR(i,x,y) for(int i=(x),i##END=(y);i<=i##END;++i)
#define DOR(i,x,y) for(int i=(x),i##END=(y);i>=i##END;--i)
typedef long long LL;
using namespace std;
const int N=1e6+5;
template<const int maxn,const int maxm>struct Linked_list
{
	int head[maxn],to[maxm],nxt[maxm],tot;
	Linked_list(){clear();}
	void clear(){memset(head,-1,sizeof(head));tot=0;}
	void add(int u,int v){to[++tot]=v,nxt[tot]=head[u],head[u]=tot;}
	#define EOR(i,G,u) for(int i=G.head[u];~i;i=G.nxt[i])
};
Linked_list<N,N>G;
int ch[N][27],f[N],occ[N];
char T[N];
char P[205][N];
int rt,tot,n,q;

void build(){rt=tot=0;}
void create(int &k)
{
	if(!k)
	{
		k=++tot;
		FOR(i,0,26)ch[k][i]=0;
		occ[k]=0;
	}
}
void insert(int &k,char *str,int len)
{
	create(k);
	int now=k;
	FOR(i,0,len-1)
	{
		create(ch[now][str[i]-'a']);
		now=ch[now][str[i]-'a'];
	}
}
void getfail()
{
	queue<int>Q;
	while(!Q.empty())Q.pop();
	f[rt]=rt;
	FOR(i,0,26)
	{
		if(ch[rt][i])f[ch[rt][i]]=rt,Q.push(ch[rt][i]);
		else ch[rt][i]=rt;
	}
	while(!Q.empty())
	{
		int u=Q.front();Q.pop();
		FOR(i,0,26)
		{
			if(ch[u][i])f[ch[u][i]]=ch[f[u]][i],Q.push(ch[u][i]);
			else ch[u][i]=ch[f[u]][i];
		}
	}
}
void dfs_fail(int u)
{
	EOR(i,G,u)
	{
		int v=G.to[i];
		dfs_fail(v);
		occ[u]+=occ[v];
	}
}
void KMP()
{
	G.clear();
	FOR(i,1,tot)if(f[i]!=i)G.add(f[i],i);
	int now=rt;
	FOR(i,0,n-1)
	{
		now=ch[now][T[i]-'a'];
		occ[now]++;
	}
	dfs_fail(rt);
}
int query(int k,char *str,int len)
{
	int now=k;
	FOR(i,0,len-1)now=ch[now][str[i]-'a'];
	return occ[now];
}

int main()
{
	build();
	scanf("%d",&q);
	char *h=T;
	FOR(i,1,q)
	{
		scanf("%s",P[i]);
		insert(rt,P[i],strlen(P[i]));
		FOR(j,0,strlen(P[i])-1)*h=P[i][j],h++,n++;
		*h='{',h++,n++;
	}
	*h='\0';
	
	getfail();
	KMP();
	FOR(i,1,q)printf("%d\n",query(rt,P[i],strlen(P[i])));
	return 0;
}