【uva 1411 Ants蚂蚁们】

题目大意：

·给你一个n，表示输入n个白点和n个黑点（输入每一个点的坐标）。现在需要将各个白点和各个黑点一一用线段连接起来，需要满足这些线段不能够相交。

·特色：

我们如何保证线段间不相交。

·分析：

由“黑白”可以想到用二分图匹配(最大流问题亦可)。用到一个神秘结论，可以巧妙地将“相交”和“不相交”转化为具体数值大小关系，进而转化为权值。结论为:【四边形两条对角线的和必定大于它任何一组对边的和】

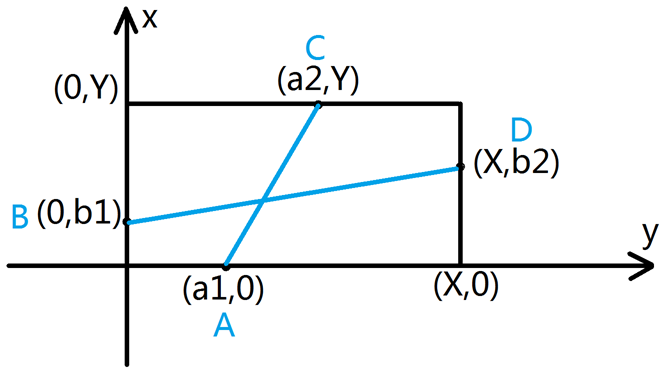
用一下这幅图进行分析：

 

         

下面来比较线段交叉和不交叉情况下，两条线段和的大小：

①交叉线段:（蓝色线段）

D1=dis(A,C)+dis(B,D)

    =(a2-a1)²+Y²+(b2-b1)²+X²

②非交叉线段(这里计算AB，CD,其余情况可以用对称性等价得到)

D2=dis(A,B)+dis(C,D)

     =a1²+b1²+(X-a2)²+(Y-b2)²

【作差】：

D1-D2=dis(A,C)+dis(B,D)-dis(A,B)-dis(C,D)

           =2*b2(Y-b1)+2*a2(X-a1)

【结论】：

由于Y==b1与X==a1同时满足是不可能的(点重合了！)

又因为Y>=b1,X>=a1所以上面D1-D2的式子必为正数。

这意味着D1恒大于D2。因此这需要我们进行最小权值的二分图完全匹配。

 

#include<stdio.h>
#include<algorithm>
#include<cstring>
#include<cmath>
#define go(i,a,b) for(int i=a;i<=b;i++)
#define fo(i,a,x) for(int i=a[x],v=e[i].v;i>-1;i=e[i].next,v=e[i].v)
#define mem(a,b) memset(a,b,sizeof(a))
#define inf 200000000
#define eps 0.000001
using namespace std;const int N=1003;
struct POS{double x,y;}white[N],black[N];
struct E{int v,next;double w;}e[N*N];
int n,head[N],k,c[N],S[N],T[N];
void ADD(int u,int v,double w){e[k]=(E){v,head[u],w};head[u]=k++;}
double A(double x){return x*x;};double slack[N],Lx[N],Ly[N];
double dis(POS a,POS b){return sqrt(A(a.x-b.x)+A(a.y-b.y));}
bool aug(int u){
    S[u]=1;fo(i,head,u)if(!T[v])
    {double t=Lx[u]+Ly[v]-e[i].w;if(t<eps&&t>-eps)
    {T[v]=1;if(!c[v]||aug(c[v])){c[v]=u;return 1;}}
    else slack[v]=min(slack[v],t);}return 0;
}
void revise(){double a=inf;
    go(i,1,n)if(!T[i])a=min(a,slack[i]);
    go(i,1,n)S[i]?Lx[i]-=a,1:1,T[i]?Ly[i]+=a,1:1;
}
int main(){while(~scanf("%d",&n)){
    mem(head,-1);k=0;
    go(i,1,n)scanf("%lf%lf",&white[i].x,&white[i].y);
    go(i,1,n)scanf("%lf%lf",&black[i].x,&black[i].y);
    go(i,1,n)go(j,1,n)ADD(i,j,-dis(white[i],black[j])); 
        
    go(u,1,n){Ly[u]=c[u]=0;Lx[u]=-inf;
    fo(i,head,u)Lx[u]=max(Lx[u],e[i].w);}
        
    go(i,1,n){go(j,1,n)slack[j]=inf;
    for(;;){go(j,1,n)S[j]=T[j]=0;
    if(aug(i))break;else revise();}}
        
    go(i,1,n)go(j,1,n)if(c[j]==i)
    {printf("%d\n",j);break;}    
}return 0;}//Paul_Guderian

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

我看见了一条河。