bzoj3672【NOI2014】购票
题目描述
今年夏天,NOI在SZ市迎来了她30周岁的生日。来自全国 n 个城市的OIer们都会从各地出发,到SZ市参加这次盛会。
全国的城市构成了一棵以SZ市为根的有根树,每个城市与它的父亲用道路连接。为了方便起见,我们将全国的 n 个城市用 1 到 n 的整数编号。其中SZ市的编号为 1。对于除SZ市之外的任意一个城市 v,我们给出了它在这棵树上的父亲城市 fv 以及到父亲城市道路的长度 sv。
从城市 v 前往SZ市的方法为:选择城市 v 的一个祖先 a,支付购票的费用,乘坐交通工具到达 a。再选择城市 a 的一个祖先 b,支付费用并到达 b。以此类推,直至到达SZ市。
对于任意一个城市 v,我们会给出一个交通工具的距离限制 lv。对于城市 v 的祖先 a,只有当它们之间所有道路的总长度不超过 lv 时,从城市 v 才可以通过一次购票到达城市 a,否则不能通过一次购票到达。对于每个城市 v,我们还会给出两个非负整数 pv,qv 作为票价参数。若城市 v 到城市 a 所有道路的总长度为 d,那么从城市 v 到城市 a 购买的票价为 dpv+qv。
每个城市的OIer都希望自己到达SZ市时,用于购票的总资金最少。你的任务就是,告诉每个城市的OIer他们所花的最少资金是多少。
输入格式
第 1 行包含2个非负整数 n,t,分别表示城市的个数和数据类型(其意义将在后面提到)。输入文件的第 2 到 n 行,每行描述一个除SZ之外的城市。其中第 v 行包含 5 个非负整数 $f_v,s_v,p_v,q_v,l_v$,分别表示城市 v 的父亲城市,它到父亲城市道路的长度,票价的两个参数和距离限制。请注意:输入不包含编号为 1 的SZ市,第 2 行到第 n 行分别描述的是城市 2 到城市 n。
输出格式
输出包含 n-1 行,每行包含一个整数。其中第 v 行表示从城市 v+1 出发,到达SZ市最少的购票费用。同样请注意:输出不包含编号为 1 的SZ市。
数据规模
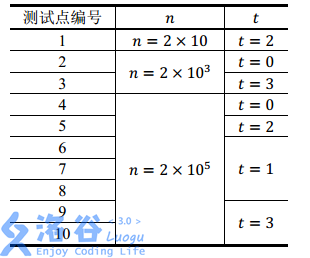
-
题解:
- 设$v$是$u$的祖先,$dp[u] = dp[v] + (dis[u]-dis[v])*p[u] + q[u] \ , \ (dis[u]-dis[v]<=l[u])$
- 斜率优化部分:
- 假设$d[v_{1}]<d[v_{2}]$且对$u$来说$v2$比$v1$更优:
- $$dp[v_{1}]+(dis[u]-dis[v_{1}])*p[u]+q[u] > dp[v_{2}]+(dis[u]-dis[v_{2}])*p[u]+q[u] ;$$
- $$\frac{dp[v_{2}]-dp[v_{1}]}{dis[v2]-dis[v1]} < p[u]$$
- 可以维护$(dis[v],dp[v])$的下凸包(斜率单调上升);
- 由于是在一颗树上且有$l$的限制,所以我们需要用用一些方法维护一下,
- 可以找树的重心分治,我写的树剖:
- 对每个重链的顶端维护一个凸包,$dfs$的时候不断加入点;
- 我们先$dfs$轻儿子,这样一个点到根的轻链的父亲都是一个凸包的末端;
- 找转移点的时候不断向上跳,如果某条链全部满足限制则在重链顶端的凸包上直接查询;
- 否则一定是合法的分界点在当前找到的链上,用线段树维护区间的凸包查询即可;
- 一次最多找到$log$条树链,最多有一条树链需要在线段树里面查询;
- 算上三分,时间复杂度:$O(nlog^2n)$
- 有个小技巧,线段树满了之后再做凸包

1 #include<bits/stdc++.h> 2 #define ls (k<<1) 3 #define rs (k<<1|1) 4 #define ll long long 5 #define ld double 6 using namespace std; 7 const int N=200010; 8 char gc(){ 9 static char*p1,*p2,s[1000000]; 10 if(p1==p2)p2=(p1=s)+fread(s,1,1000000,stdin); 11 return(p1==p2)?EOF:*p1++; 12 } 13 ll rd(){ 14 ll x=0; char c=gc(); 15 while(c<'0'||c>'9')c=gc(); 16 while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+c-'0',c=gc(); 17 return x; 18 } 19 int n,T,f[N],o=1,hd[N],dep[N],fa[N][20],bin[20]; 20 int idx,sz[N],tp[N],sn[N],mx[N],id[N],cnt[N<<2],st[N]; 21 ll dp[N],tmp,dis[N],s[N],p[N],q[N],l[N]; 22 struct Poi{ 23 ld x,y; 24 Poi(ld _x=0,ld _y=0):x(_x),y(_y){}; 25 Poi operator -(const Poi&a){return Poi(x-a.x,y-a.y);} 26 ld operator ^(const Poi&a){return x*a.y-y*a.x;} 27 bool operator <(const Poi&a){return x==a.x?y<a.y:x<a.x;} 28 }P[N]; 29 vector<int>g1[N<<2],g2[N]; 30 struct Edge{int v,nt;}E[N]; 31 void adde(int u,int v){E[o]=(Edge){v,hd[u]};hd[u]=o++;} 32 void dfs1(int u){ 33 sz[u]=1; 34 fa[u][0]=f[u]; 35 dep[u]=dep[f[u]]+1; 36 dis[u]=dis[f[u]]+s[u]; 37 for(int i=1;bin[i]<dep[u];++i)fa[u][i]=fa[fa[u][i-1]][i-1]; 38 for(int i=hd[u];i;i=E[i].nt){ 39 int v=E[i].v; 40 dfs1(v); 41 sz[u]+=sz[v]; 42 if(sz[v]>sz[sn[u]])sn[u]=v; 43 } 44 } 45 void dfs2(int u,int t){ 46 tp[u]=t; 47 id[u]=++idx; 48 st[idx]=u; 49 if(sn[u])dfs2(sn[u],t); 50 for(int i=hd[u];i;i=E[i].nt){ 51 int v=E[i].v; 52 if(v==sn[u])continue; 53 dfs2(v,v); 54 } 55 } 56 inline bool judge(int a,int b,int c){return ((P[b]-P[a])^(P[c]-P[b]))<=0;} 57 void pushup(int k){ 58 int l=ls,r=rs,tl=0,tr=0; 59 while(tl<(int)g1[l].size()||tr<(int)g1[r].size()){ 60 if(tr==(int)g1[r].size()||(tl<(int)g1[l].size()&&g1[l][tl]<g1[r][tr])){ 61 while(g1[k].size()>1&&judge(g1[k][g1[k].size()-2],g1[k].back(),g1[l][tl]))g1[k].pop_back(); 62 g1[k].push_back(g1[l][tl++]); 63 }else{ 64 while(g1[k].size()>1&&judge(g1[k][g1[k].size()-2],g1[k].back(),g1[r][tr]))g1[k].pop_back(); 65 g1[k].push_back(g1[r][tr++]); 66 } 67 } 68 } 69 void ins1(int k,int l,int r,int u){ 70 cnt[k]++; 71 if(l==r){g1[k].push_back(u);return;} 72 int mid=(l+r)>>1; 73 if(id[u]<=mid)ins1(ls,l,mid,u); 74 else ins1(rs,mid+1,r,u); 75 if(tp[st[l]]==tp[st[r]]&&cnt[k]==r-l+1)pushup(k); 76 } 77 void ins2(int k,int u){ 78 while(g2[k].size()>1&&judge(g2[k][g2[k].size()-2],g2[k].back(),u))g2[k].pop_back(); 79 g2[k].push_back(u); 80 } 81 inline bool ok(int u,int v){return dis[u]-dis[v]<=l[u];} 82 inline void upd(ll&x,ll y){if(x>y)x=y;} 83 void cal(vector<int>&g,int u){ 84 int l=0,r=g.size()-1; 85 while(r-l>2){ 86 int mid=(r-l)/3,mid1=l+mid,mid2=r-mid; 87 ll t1=dp[g[mid1]]-dis[g[mid1]]*p[u]; 88 ll t2=dp[g[mid2]]-dis[g[mid2]]*p[u]; 89 if(t1>t2)l=mid1+1; 90 else r=mid2-1; 91 } 92 for(int i=l;i<=r;++i)upd(tmp,dp[g[i]]-dis[g[i]]*p[u]); 93 } 94 void query1(int k,int l,int r,int x,int y,int u){ 95 if(l==x&&r==y){cal(g1[k],u);return;} 96 int mid=(l+r)>>1; 97 if(y<=mid)query1(ls,l,mid,x,y,u); 98 else if(x>mid)query1(rs,mid+1,r,x,y,u); 99 else query1(ls,l,mid,x,mid,u),query1(rs,mid+1,r,mid+1,y,u); 100 } 101 void query2(int x,int u){ 102 cal(g2[x],u); 103 } 104 void solve(int u){ 105 tmp=u==1?0:9e18; 106 for(int x=f[u],t=tp[x];x;x=f[t],t=tp[x]){ 107 if(dep[mx[u]]<dep[t])query2(id[t],u); 108 else {query1(1,1,n,id[mx[u]],id[x],u);break;} 109 } 110 dp[u]=dis[u]*p[u]+q[u]+tmp; 111 P[u]=Poi(dis[u],dp[u]); 112 ins1(1,1,n,u); 113 ins2(id[tp[u]],u); 114 } 115 void calmx(int u){ 116 int t=u; 117 for(int i=17;~i;--i)if(fa[t][i]&&ok(u,fa[t][i]))t=fa[t][i]; 118 mx[u]=t; 119 } 120 void dfs3(int u){ 121 calmx(u); 122 solve(u); 123 for(int i=hd[u];i;i=E[i].nt){ 124 int v=E[i].v; 125 if(v==sn[u])continue; 126 dfs3(v); 127 } 128 if(sn[u])dfs3(sn[u]); 129 } 130 int main(){ 131 #ifndef ONLINE_JUDGE 132 freopen("bzoj3672.in","r",stdin); 133 freopen("bzoj3672.out","w",stdout); 134 #endif 135 for(int i=bin[0]=1;i<=18;++i)bin[i]=bin[i-1]<<1; 136 n=rd();T=rd(); 137 for(int i=2;i<=n;++i){ 138 adde(f[i]=rd(),i); 139 s[i]=rd();p[i]=rd(); 140 q[i]=rd();l[i]=rd(); 141 } 142 dfs1(1); 143 dfs2(1,1); 144 dfs3(1); 145 for(int i=2;i<=n;++i)printf("%lld\n",dp[i]); 146 return 0; 147 }


