树链剖分I 原理

有根树

任意指定无根树的某个顶点 $v$ 作为根便得到有根树。下面只讨论有根树。把点 $u$ 和其父亲之间的边称为 $u$ 的父边；除根节点外，点 $u$ 和 $u$ 的父边一一对应。

有根树结构的核心特征是每个节点有唯一前驱，但有多个后继。线性结构的核心特征是每个节点有唯一前驱和唯一后继。
若能给每个节点指定一个“唯一”后继，就能把有根树划分成若干条链。

重儿子与重边

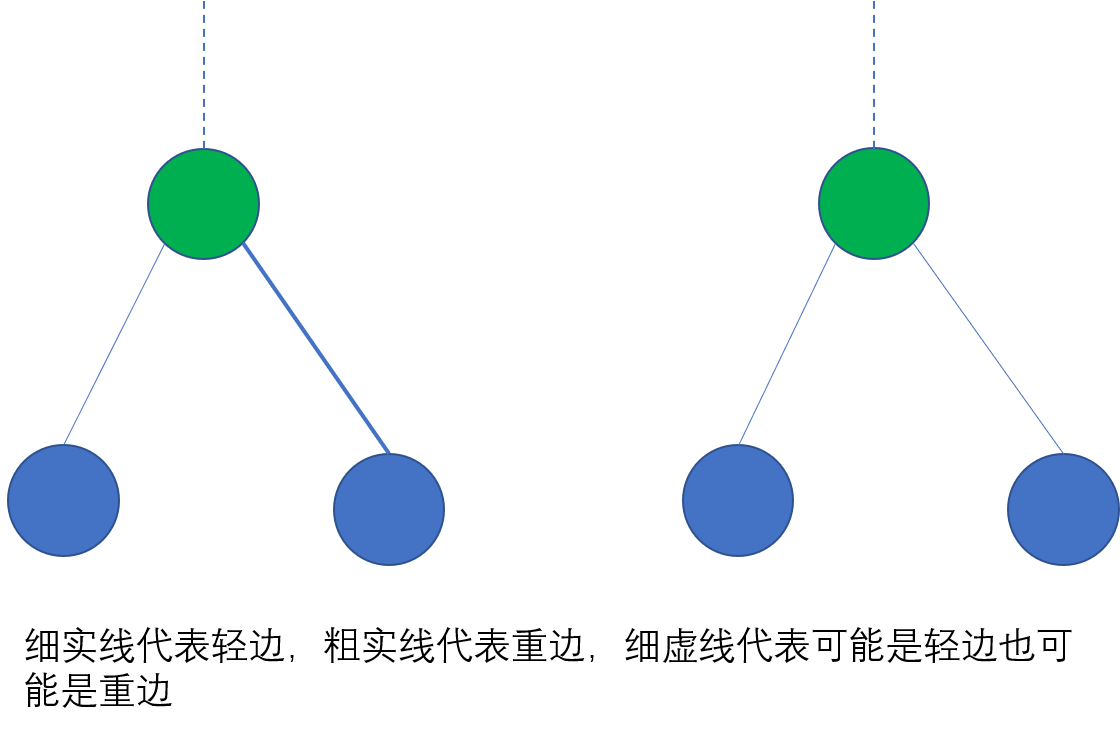
$u$ 的所有儿子中，以之为根的子树中节点数最多者称为 $u$ 的重儿子（heavy son），若有多个儿子可以作为重儿子，任取一个，其余儿子称为轻儿子（light son）；$u$ 与其重儿子之间的边称为重边，与其轻儿子之间的边称为轻边。

重节点与轻节点

若非根节点 $u$ 是其父亲的重儿子，则称其为重节点。不是重节点的点称为轻节点，特别地，根是轻节点。

重链

以某个轻节点为起点，沿着重儿子扩展，直到某个叶子节点，将得到一个节点序列，这样的点列称为重链。在不至引起混淆的情况下，也把由这样的点列所导出的子图称为重链。

重链的性质

1. 根据定义，重链的链首是轻节点。

2. 对于一棵 $n$ 个节点的树，从根到任意叶子节点所经过的重链数目不超过 $\log n$。

---

以下内容较为粗糙，需要改进。

树链剖分（Heavy Light Decomposition, HLD）是一种将对【树上两点间的路径】上【边或点】的【修改与查询】转化到【序列】上来处理的方法。

目的：将树的点或边转化到一个线性结构（序列）上。

方法：指定点或边的唯一后继。对于任意非叶子节点 $u$，指定 $u$ 的重儿子作为 $u$ 的唯一后继。类似地指定边的唯一后继。

如何将对「树上路径」的修改操作转化到线性结构上？

深度优先遍历。重链在 DFS 序列中是连续的。

轻节点是重链的起点。

树链剖分的精髓：
「有根树」结构的核心特征是：每个节点有唯一前驱，但有多个后继。线性结构的核心特征是每个节点有唯一前驱和唯一后继。
现在采用轻重划分，给每个节点找到一个特殊的“唯一”后继，就相当于在树结构上增加了线性成分，或者说把树往序列转化。

形式化地说，树链剖分是下述剖分问题的一个方案（解法）

将树 $T=(V, E)$ 的点集 $V$ 划分成 $m$ 个不相交的非空子集 $V_1, V_2, \cdots,V_m$ 使得每个点集的导出子图是一条链.

 

HLD 具有以下性质：

从根节点到任一节点所经过的上述子集 $V_i$ 的数目为 $O(\log{n})$ , $n$ 是树的节点数.

 

HLD 路径分解的注意事项

在 HLD 的代码实现中，基本的操作是将 $u$ 到 $v$ 的路径分解到事先划分好的若干个链上。

需要区别两种情况，一种是数据存在边上，另一种是数据存在点上。